1. 引言
鱼雷寿命分布函数的确定是鱼雷装备可靠性评估中的重要问题。目前装备寿命分布的确定一般采用多种模型拟合择优法。利用失效数据对常用的几种寿命分布进行拟合优度检验 [1] [2] ,确定最佳的寿命分布模型。
目前研究寿命分布拟合的方法较多,不同的拟合方法其计算出的结果和误差区别较大。文献 [3] [4] [5] 凭借积累经验选择分布具有较大的不确定性。在实践中运用较多的矩估计法和图估计法 [6] ,虽计算方法简单,但两种方法不仅对失效数据的样本量要求较大,而且计算精度较低,易受主观因素的影响。文献 [7] 分别运用极大似然估计和最小二乘法对三种失效分布进行拟合,通过实例比较确定了失效分布,但最小二乘法对数据不敏感。
对于投入部队使用很长时间的鱼雷,其数据量较大。依据中心极限定理,当测量数据样本达到一定数量时,估计得到的参数值与参数真值误差很小,具有较高的可信度。本文针对数据量较大的某型鱼雷贮存过程中的失效数据的特点,用极大似然估计法和极小χ2估计法分别对常用的几种常见分布进行参数估计和分布拟合,分析拟合结果,选择较好的拟合方法,确定鱼雷装备的寿命分布函数。
2. 可靠性数据结构
随着贮存时间的增加,受贮存环境的影响,鱼雷可靠性逐渐降低。在贮存过程中会定期对鱼雷进行全面的技术检测,确认装备是否发生故障,记录检测结果。对于在部队服役时间较长的某型鱼雷,根据检测记录结果。统计从服役开始到时刻
时间段内某型鱼雷的总数
中未失效的数量为
,失效数为
,统计的可靠性数据结构为
(1)
设鱼雷装备的贮存寿命为T,则T的寿命分布函数为:
(2)
式中,
为贮存可靠度。
检测统计结果中未失效数据
可以看作是一个服从
的二项分布的样本,且
,则可以用
时刻
的极大似然估计对
进行估计,即
(3)
3. 参数估计
3.1. 常见的分布类型
假设
是分布族,
为参数空间,根据鱼雷装备贮存可靠性的相关研究,鱼雷常见的寿命分布有下列4种:
1) 指数分布:
2) 威布尔分布:
3) 极值分布:
4) 对数正态分布:
文中利用极大似然估计法和极小卡方估计法对4种分布分别进行参数估计和拟合优度检验,确定最佳的寿命分布作为鱼雷装备的贮存寿命分布函数,并比较两者的优劣。
3.2. 极大似然估计
失效数r为随机变量,服从二项分布,则似然函数为
(4)
极大似然估计就是选取使得似然函数达到最大的数值作为参数的估计值 [8] ,即寻找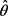 使得
成立。
使得
成立。
对于指数分布:
其似然方程为
(5)
对于威布尔分布:
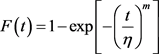
其似然方程为
(6)
对于极值分布:
其似然方程为
(7)
对于对数正态分布:
其似然方程为
(8)
通过计算机编程等方法可以求得各个分布的参数估计,从而确定假定的装备寿命分布的形式。
3.3. 极小卡方估计法
1) 构造χ2统计量
鱼雷的寿命分布为
,设
,基于统计数据 ,则
,则
(9)
当
时,根据中心极限定理得:
(10)
对式(5)两边取平方,将式(3)带入可得:
(11)
令
(12)
当
时,
统计量的渐近分布是自由度为k的χ2分布。
2) 参数估计
待估参数
的估计
若满足
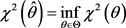 (13)
(13)
称
为参数
的极小χ2估计,则对
统计量求关于
的最小值,就可得到参数
的估计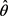 。
。
4. 拟合优度检验
利用极大似然估计和极小χ2估计的参数估计结果分别对4种分布函数构造χ2统计量,进行拟合优度检验,由于4种分布族的待估计参数数量不同,设各个分布的待估参数数量为m,则对于各个分布的χ2统计量的渐近分布的自由度为
。
拟合优度p为:
(14)
拟合优度p值衡量假定分布与统计样本数据的拟合程度,p值越大,拟合程度越好,所以可以通过比较4种分布情况下的p值来确定最佳的寿命分布。
5. 拟合方法的评判
设利用两种拟合方法确定的最佳寿命分布函数分别求得鱼雷装备的贮存可靠度为
,统计数据得到的可靠度为
,两者的相对误差为:
(15)
则相对误差的标准差估计为:
(16)
将标准差估计S作为评价两种寿命分布拟合方法优劣的标准,S值越小则说明该种拟合方法较好。
6. 实例计算与分析
6.1. 数据来源及结构
以目前服役的某型全部鱼雷作为样本总体,统计从投入部队到时刻
时间段内鱼雷出现故障的条数,统计结果如表1所示。

Table 1. Storage life data of torpedo equipment
表1. 鱼雷装备贮存寿命数据
6.2. 参数估计和拟合优度检验
1) 极大似然估计
利用极大似然估计拟合方法计算4种寿命分布的参数估计和拟合优度值如表2所示。

Table 2. The calculated results of maximum likelihood estimation and goodness of fit test
表2. 极大似然估计拟合方法计算结果
从表2中可以看出,极值分布的拟合优度值最大,拟合效果最好,则该型鱼雷装备的最佳的寿命分布函数为:
(17)
极大似然估计拟合方法得到的不同分布类型贮存可靠度的函数曲线如图1所示。
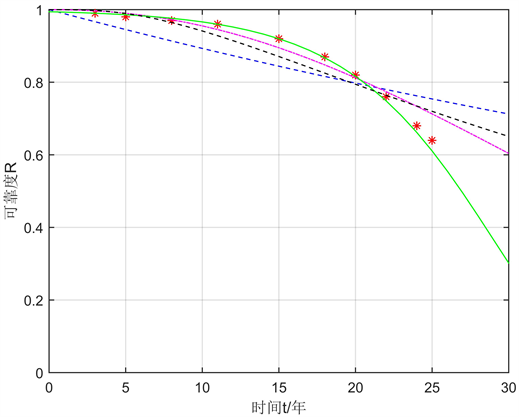
Figure 1. The effect of maximum likelihood fitting estimation
图1. 极大似然估计拟合效果
从图1中可以看出,极值分布与统计的寿命数据得到的可靠度之间拟合程度最好。
2) 极小χ2估计拟合方法
利用极小χ2估计拟合方法计算4种寿命分布的参数估计和拟合优度值如表3所示。
从表3中可以看出,极值分布的拟合优度值最大,拟合效果最好,则该型鱼雷装备的最佳的寿命分布函数为:
(18)
极小卡方估计拟合方法得到的不同分布类型贮存可靠度的函数曲线如图2所示。

Table 3. The calculated results of minimum χ2 estimation fitting method
表3. 极小卡方估计拟合方法计算结果
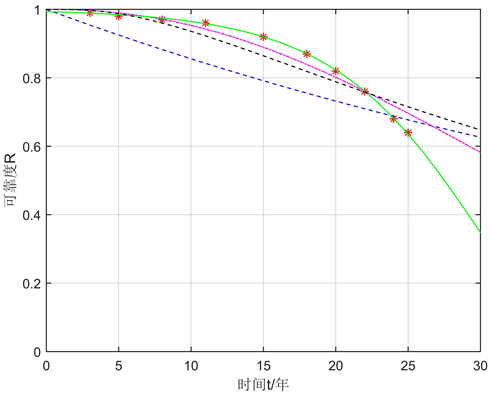
Figure 2. The effect of minimum χ2 estimation fitting method
图2. 极小χ2估计拟合效果
从图2中可以看出,极值分布与统计的寿命数据得到的可靠度之间拟合程度最好。
6.3. 拟合方法比较分析
1) 相对误差标准差计算及分布函数曲线
两种方法确定装备的寿命分布函数均服从极值分布,因此可以得到装备随时间增加的贮存可靠度,通过计算得到两种拟合方法的
和
相对误差的标准差分别为
,因为
,则认为极小χ2估计方法拟合效果较好。
极大似然估计拟合法和极小χ2估计拟合法得到的装备寿命分布函数如图3所示。
2) 拟合方法比较分析
两种拟合方法得到的装备最佳寿命分布函数相同,结合拟合优度值和相对误差标准差可以看出,相对极大似然估计拟合方法,极小χ2估计拟合法的拟合优度值更大,相对误差标准差更小。从函数曲线上可以看出极小χ2估计拟合方法得到的曲线拟合程度更高,所以对于鱼雷装备寿命分布拟合而言,极小χ2估计拟合方法效果更好。

Figure 3. Comparison of the two estimation methods
图3. 两种估计拟合方法对比
7. 结论
针对部队服役时间较长、数据量较大的某型鱼雷寿命数据的特点,分别利用极大似然估计拟合方法和极小χ2估计拟合方法对装备寿命分布进行参数估计和分布拟合。通过比较分析得出极小χ2估计拟合方法拟合效果更好,更加准确反映鱼雷装备可靠性变化规律。极小χ2估计拟合方法较极大似然估计方法而言,程序化较好,应用较为方便,更适合鱼雷装备寿命分布拟合。
基金项目
“十三五”水中兵器预先研究项目(3020605030302)。
NOTES
*通讯作者。