1. 引言
为满足对轨道交通振动控制的需要，在地铁线路上大量采用了不同等级的轨道减振措施 [1] 。随着减振扣件轨道、梯形轨枕轨道、套靴轨枕轨道、钢弹簧浮置板轨道、橡胶浮置板轨道等新型减振轨道的大面积使用，我国北京、广州、上海、深圳等城市地铁线路钢轨波磨现象越来越严重 [2] 。钢轨波磨会增强轮轨相互作用，造成车内噪声增大，减振轨道的减振性能下降，有必要在现有地铁轨道与车辆设计的基础上考虑波磨的影响。
在众多新型减振轨道中，钢弹簧浮置板轨道系统由于其减振效果明显、隧道几何空间利用效率高、养护维修方便等优点在特殊减振地段被广泛采用。从工程设计角度出发，在满足设计要求的前提下，兼顾钢弹簧浮置板轨道地段钢轨波磨的预防和治理，需要系统的掌握车辆与钢弹簧浮置板轨道之间的相互作用特征。
目前，国内外学者对于钢弹簧浮置板系统的振动特性研究主要集中在其垂向振动特性的研究，通常将钢弹簧浮置板系统视为离散点支承上的欧拉梁模型、Timoshenko梁模型或连续支承的Winkler地基梁模型 [3] [4] [5] ，或采用ANSYS有限元软件建立浮置板轨道的有限元模型，进行模态和减振性能分析 [6] [7] [8] ，这些研究对掌握钢弹簧浮置板垂向振动特性，了解动力学参数对浮置板减振性能的影响规律具有很大的促进作用。但这些研究主要研究钢弹簧浮置板自身的振动特性和减振性能，对车辆与钢弹簧浮置板轨道之间的相互作用关系缺乏系统的研究，无法反应浮置板减振性能与车辆运行品质之间的相互影响关系，不利于掌握车辆–钢弹簧浮置板轨道相互作用规律。
本文基于车辆–轨道耦合动力学理论，建立车辆–钢弹簧浮置板轨道动力相互作用空间模型，分析地铁车辆在通过钢弹簧浮置板轨道时整个系统的振动特性，以期为钢弹簧浮置板的动力参数设计和车辆运行品质评估提供参考，为工程设计提供计算手段。
2. 车辆–钢弹簧浮置板轨道动力相互作用空间模型
基于车辆–轨道耦合动力学理论 [9] ，建立车辆–钢弹簧浮置板轨道动力相互作用空间模型，如图1所示。在该空间模型中，车辆模型为整车模型，针对地铁中常用的车辆进行建模，包括一个车体、两个构架和四个轮对。其中车体、构架和轮对均按刚体考虑，不靠虑其弹性变形，车辆沿线路方向作等速运动，不考虑相邻车辆间的纵向动力作用，不考虑车辆的伸缩振动，一系和二系悬挂装置的质量等效在构架侧架上，其刚度和阻尼均视为线性，车体前后左右对称，转向架构架左右对称。基于以上假定，车辆模型中车体、构架和轮对均考虑垂向、横向、侧滚、摇头、点头五个运动自由度，每一车辆共有35个自由度。
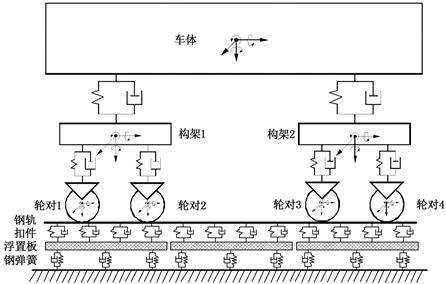(a) 正视图 
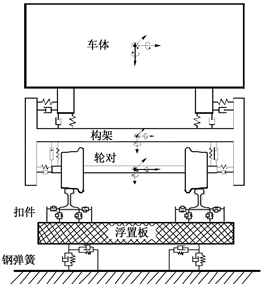(b) 侧视图
Figure 1. Spatial model of vehicle-steel spring floating plate interaction
图1. 车辆–钢弹簧浮置板相互作用空间模型
对于空间模型的其他部分，轮轨相互作用关系采用轮轨空间动态耦合模型，钢轨采用Euler模型，考虑其垂向、横向和扭转振动，扣件按支承位置简化为离散的线性点弹簧和阻尼。钢弹簧浮置板的垂向按边界自由的等厚度矩形薄板考虑，而横向视为刚体运动 [10] 。钢弹簧考虑其垂向与横向的刚度与阻尼，简化为离散的线性点弹簧和阻尼。在本模型中，仅考虑直线段情况，并假设车辆匀速运行。
3. 仿真参数
3.1. 车辆参数
车辆选用地铁车辆动力学参数，采用6辆编组，编组形式为4动2拖，其中拖车的动力学计算参数如表1所示。车辆运行速度设为40 km/h、60 km/h、80 km/h和100 km/h。
Table 1. Dynamic parameters of metro vehicle
表1. 地铁车辆动力学参数
3.2. 轨道参数
钢弹簧浮置板轨道的动力学计算参数如表2所示 [11] [12] 。为消除边界条件的影响，钢弹簧浮置板轨道取8块，不考虑相邻浮置板道床间接缝处的剪力铰。在计算时轨道板长度方向的模态取到第8阶，轨道板宽度方向的模态取到第4阶。对于整个系统，利用新型显式二步积分法进行求解 [13] ，积分步长取0.0001 s。
Table 2. System resulting data of standard experiment
表2. 轨道参数
3.3. 轨道不平顺激励
目前地铁没有对应的轨道不平顺谱，结合地铁车辆的运行速度和地铁线路的特点，轮轨间的激励采用美国六级轨道不平顺谱，波长1 m~80 m，采用逆傅里叶法进行变换 [14] ，得到随里程变化的轨道不平顺如图2所示。另外，设置以80 km/h的速度运行时，无轨道不平顺激励的对比工况。
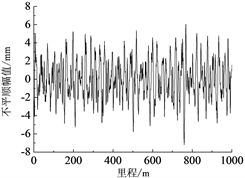(a) 左侧轨向 
(b) 右侧轨向 
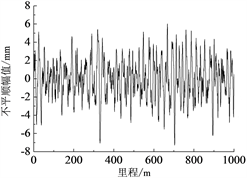(c) 左侧高低 
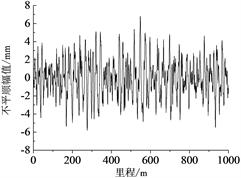(d) 右侧高低
Figure 2. Track irregularity
图2. 轨道不平顺
4. 仿真结果与分析
4.1. 典型时程曲线分析
在80 km/h速度下，无轨道不平顺激励时，车辆第一位轮对左侧轮轨力与车体振动加速响应的时程曲线分别如图3和图4所示。由图3可知，第一轮对的轮轨力大小随着车辆的运行呈现周期性的变化，出现了9个周期性峰值，这是由钢轨下方垂向支承刚度沿纵向的周期性变化引起的。在车辆驶进和驶出钢弹簧浮置板区域时，钢轨下方支承刚度发生突变，造成轮轨力出现第1个和第9个峰值，在两个相邻的轨道板之间存在间隙，沿钢轨纵向的垂向支承刚度由于轨道板的不连续而在间隙处发生变化，当车辆依次通过8块轨道板之间的7个间隙时，由于刚度的变化造成轮轨力的变化，从而产生图3中第1个和第9个峰值之间的另外7个峰值。另一方面，由于垂向支承刚度的变化要远大于横向支承刚度的变化，因此轮轨垂向力的变化要大于轮轨横向力的变化。
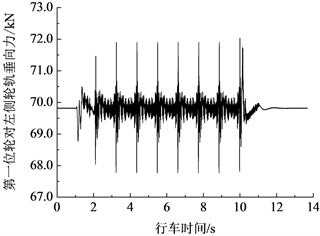(a) 垂向 
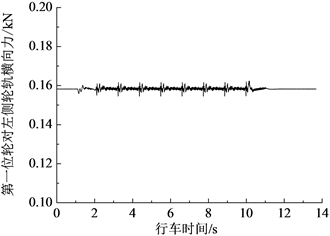(b) 横向
Figure 3. Wheel-rail force response under non-track irregularity
图3. 无轨道不平顺激励条件下的轮轨力响应
由图4可知，车体的垂向加速度和横向加速度也随着车辆的运行呈现周期性的变化，出现9个峰值。产生这种现象的原因与产生轮轨力周期性变化的原因相同，在此不再重复介绍。
(a) 垂向
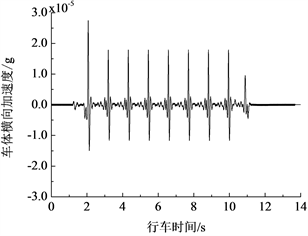(b) 横向
Figure 4. Acceleration response of car body without track irregularity
图4. 无轨道不平顺激励条件下的车体加速度响应
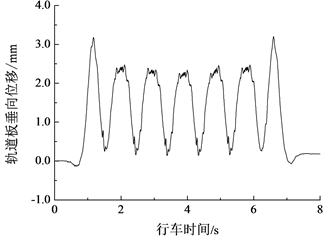
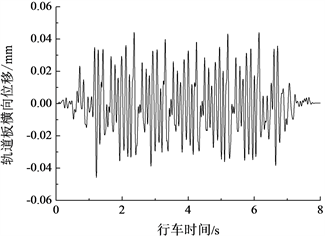
在80 km/h速度下，轮轨之间加上轨道不平顺激励后，轨道板的垂向、横向与沿纵向中心轴转动的振动时程曲线分别如图5~图7所示，其中，图5是浮置板上中间位置钢弹簧支承点处的响应，轨道板在横向和转动方向被假定位刚体，图6与图7给出了轨道板的整体响应。由图5~图7可知，浮置板的振动时程曲线呈现周期性变化，由车辆定长对应频率引起的周期性强迫振动比较明显。另外，由于是在直线地段，轨道板横向受力大体上呈现对称性，因此轨道板横向振动和沿纵向中心轴转动的响应幅值相对于垂向振动的响应幅值而言均比较小。在下文的分析中，轨道板的振动主要针对垂向响应进行。
(a) 位移
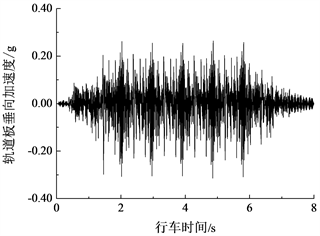(b) 加速度
Figure 5. Vertical vibration response of floating-slab
图5. 浮置板轨道垂向振动响应
(a) 位移 
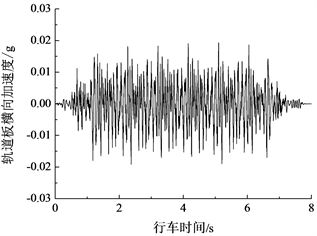(b) 加速度
Figure 6. Transverse vibration response of floating-slab
图6. 浮置板轨道横向振动响应
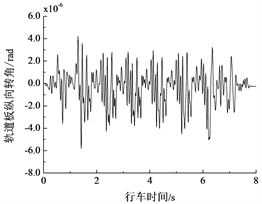(a) 位移
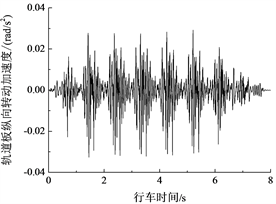(b) 加速度
Figure 7. Longitudinal rotation response of floating-slab
图7. 浮置板轨道沿纵向转动响应
4.2. 随速度变化规律
在轨道不平顺激励下，车辆以不同速度通过钢弹簧浮置板轨道时，车辆的动力学指标最大值统计和评判结果如表3所示，轨道板的垂向振动响应统计结果如表4所示。由表3可知，车辆的各项动力学指标均随着行车速度的增加而增加，当行车速度从40 km/h增加到60 km/h时，车辆各项动力学指标的增加量，明显大于行车速度从60 km/h增加到80 km/h以及从80 km/h增加到100 km/h时，各项对应动力学指标的增加量。总体上来看，在计算速度范围内，车辆的各项动力学指标均满足《铁道车辆动力学性能评定和鉴定规范》(GB5599-85)的要求 [15] ，安全性指标均合格，并且有较大的余量。
Table 3. Maximum statistics and evaluation results of vehicle dynamics indicators
表3. 车辆动力学指标最大值统计和评判结果
Table 4. Vertical vibration response amplitude of floating-slab
表4. 浮置轨道板垂向振动响应幅值
由表4可知，浮置板轨道的垂向位移、垂向加速度、垂向加速度有效值和振动加速度级，均随着行车速度的增加而增加。表4中，轨道板动力响应对应的位置为浮置板上中间位置钢弹簧支承点处，与图5相同，轨道板加速度有效值和振动加速度级对应的频率范围为1 Hz~200 Hz，不同速度条件下振动加速度级的三分之一倍频程如图7所示。由当单节车辆静止放置在一块钢弹簧浮置板中间位置时，钢弹簧的静态压缩量为2.06 mm，对比表4中浮置板的位移最大值可知，由车辆的动力荷载产生的动位移的变化范围为1.060 mm~1.148 mm。与车辆各项动力学指标增量随行车速度增量的变化规律相同，当行车速度从40 km/h增加到60 km/h时，浮置板轨道垂向动力响应的增加量，明显大于行车速度从60 km/h增加到80 km/h以及从80 km/h增加到100 km/h时，各项对应动力学指标的增加量。综合表3与表4的情况来看，车辆与浮置板未发生共振情况。
浮置板振动加速度级如图8所示。由图8可知，在1 Hz~200 Hz范围内，对应40 km/h、60 km/h、80 km/h和100 km/h的行车速度，轨道板振动加速度峰值对应的三分之一倍频程中心频率分别20 Hz、31.5 Hz、40 Hz和100 Hz，说明随着行车速度的增加，轨道板垂向振动加速度级的卓越频带，发生了向高频移动的现象。同时，由图7可知，在1 Hz~200 Hz频率范围内，轨道板垂向振动加速度级在各三分之一倍频程频带上，大体上按照行车速度的高低由大到小变化，在个别频带上，存在低速时的加速度级比高速时的加速度级大的情况。
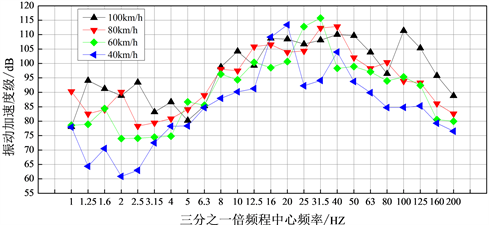
Figure 8. Vibration acceleration level of floating-slab
图8. 浮置板振动加速度级
图9为80 km/h条件下，有、无轨道不平顺激励条件时浮置轨道板振动加速度级在各频带上的分布情况。由图9可知，有、无轨道不平顺激励时，轨道板振动加速度级在以50 Hz和63 Hz的两个频带内区别比较明显，同样的，相同条件下，当速度为60 km/h时，轨道板振动加速度级在以40 Hz和80 Hz的两个频带内区别比较明显，当速度为100 km/h时，轨道板振动加速度级在以63 Hz和100 Hz的两个频带内区别比较明显，说明这40 Hz~100 Hz频带的能量主要由轮轨相互作用产生，在进行钢弹簧浮置板动力性能设计时，应关注这个频带内系统的动力特性。
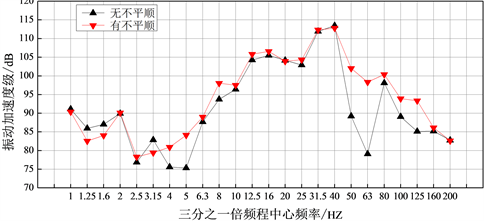
Figure 9. Vibration acceleration level of floating-slab under non-track irregularity
图9. 无不平顺激励条件下浮置板振动加速度级
4.3. 钢弹簧垂向支承刚度对系统动力响应的影响
钢弹簧垂向支承刚度直接决定了钢弹簧浮置板的隔振性能。为了分析钢弹簧垂向支承刚度的变化对车辆–钢弹簧浮置板轨道相互作用系统动力响应的影响，分别将钢弹簧垂向支承刚度设置为原刚度的1/4、1/2、2和4倍，即将刚度分别设为1.65 × 106 N/m、3.3 × 106 N/m、6.6 × 106 N/m、1.32 × 107 N/m和2.64 × 107 N/m，仿真分析有、无轨道不平顺激励时车辆–钢弹簧浮置板动力相互作用系统的响应。
图10为80 km/h条件下，无不平顺激励时，在原支承刚度和4倍支承刚度条件下，车辆第一位轮对左侧轮轨力时程响应的对比情况。由图9可知，当支承刚度变为原来的4倍后，轮轨垂向力的最大值与最小值均减小了约1.5 kN，幅值的变化范围明显减小，说明轮轨之间的相互作用减弱，反过来讲，即支承刚度减小，轮轨相互作用增强。
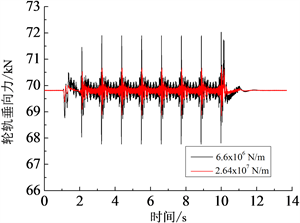
Figure 10. Vertical force of wheel and rail under different supporting stiffness of steel spring
图10. 钢弹簧垂向不同支承刚度条件下的轮轨垂向力
图11为施加轨道不平顺激励后，车体垂向加速度与轨道板垂向加速度随钢弹簧垂向支承刚度的变化情况。由图可知，车体垂向加速度与轨道板垂向加速度均随着钢弹簧支承刚度的增加而减少。结合图9的现象分析可知，随着支承刚度的减小，在质量不变的情况下，钢弹簧浮置板的隔振频率降低，即车辆运行时产生的振动能量向下传递的份额减少，保留在钢弹簧以上的能量增加，造成轮轨相互作用力增强，车体和轨道板的振动增大。因此在设计钢弹簧浮置板系统的隔振性能时，应综合考虑其对车辆动力响应、轨道动力性响应、轮轨相互作用的影响。
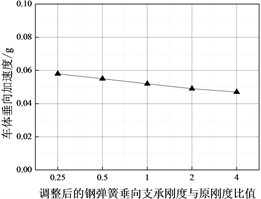(a) 车体 
(b) 浮置板
Figure 11. Influence of vertical stiffness of steel spring on dynamic response of interaction system
图11. 钢弹簧垂向支承刚度的变化对相互作用系统动力响应的影响
5. 结论
本文基于车辆–轨道耦合振动理论，建立了地铁车辆–钢弹簧浮置板轨道动力相互作用空间模型，通过设置不同工况，仿真分析了车辆–钢弹簧浮置板轨道相互作用系统的动力响应。在本文的计算条件下，得到如下结论：
1) 车辆定长引起的周期性激励和浮置板轨道接缝处产生的周期性支承刚度变化，会应引起车辆–钢弹簧浮置板轨道相互作用系统的周期性动力响应。
2) 车辆以不大于100 km/h的速度通过钢弹簧浮置板轨道时，车辆的安全性指标均合格，平稳性指标为优秀，车辆与浮置板没有发生共振情况。
3) 随着行车速度的增加，轨道板垂向振动加速度级的卓越频带向高频移动，在进行钢弹簧浮置板动力性能设计时，应关注40 Hz~100 Hz频带范围内系统的轮轨相互作用。
4) 轮轨相互作用随着钢弹簧垂向支承刚度的减小而增强，车体和轨道板的振动随着钢弹簧垂向支承刚度的减小而增加，在进行钢弹簧浮置板减振性能设计时，应综合考虑整个系统的动力特性。
5) 有必要开展针对车辆–钢弹簧浮置板轨道相互作用动力响应的追踪实测，为在工程设计中兼顾钢轨波磨的预防和治理提供数据支持。
基金项目
中国铁路设计集团有限公司科技开发课题《城市轨道交通减振试验场设计技术与试验技术研究》(721740)、《城市地下铁路减隔振技术研究》(7217131)。