多层高温作业服装模型的研究

doi:10.12677/MOS.2019.81004

期刊菜单

多层高温作业服装模型的研究
Research on Multi-Layer High Temperature Work Clothing Model

DOI: 10.12677/MOS.2019.81004, PDF, HTML, XML,
作者: 高佳丰, 赵之：山东科技大学，土木工程与建筑学院，山东青岛
关键词: 热传递模型；常微分方程；数值解；Heat Transfer Model； Ordinary Differential Equation； Numerical Solution

摘要: 物体或系统内各点间的温度差存在是产生热传导的必要条件，由热传导方式引起的传热速率(称为导热速率)决定于物体内温度的分布情况。热传导的机理较复杂，1822年，法国数学家Fourier对导热数据和实践经验的提炼，将导热规律总结为傅立叶定律。对于一定厚度的均匀介质，若两侧存在温差，则单位时间内由温度高的一侧向温度低的一侧通过单位面积的热量与两侧温差成正比，与均质厚度成反比。比热容是单位质量物体改变单位温度时吸收或放出的热量。经问题分析，我们建立出多层防护衣模型，并采用微分方程法对每层进行分析求解。经检阅资料，热传导还包括着各种参数的隐形影响。其中辐射传热对参数影响最大。所以在模型的优化上，我们主要在自身建立的多层高温作业服模型的基础上，加进对辐射热参数的优化。

Abstract: The temperature difference between objects in an object or system is a necessary condition for generating heat conduction and the heat transfer rate (called heat conduction rate) caused by the heat conduction method is determined by the temperature distribution inside the object. The mechanism of heat conduction is more complicated. In 1822, French mathematician Fourier refined the heat conduction data and practical experience, and summarized the heat conduction law as Fourier’s law. For a uniform medium of a certain thickness, if there is a temperature difference between the two sides, the heat per unit area from the side with a high temperature to the side with a low temperature per unit time is proportional to the temperature difference between the two sides, and is inversely proportional to the thickness of the homogeneous. Specific heat capacity is the amount of heat absorbed or released by a unit mass object when it changes its unit temperature. After the problem analysis, we built a multi-layer protective clothing model and analyzed and solved each layer by differential equation method. For the first problem, heat conduction per unit area per unit time can be obtained, and the heat obtained per layer per unit time is the heat obtained from the previous layer minus the heat transferred to the next layer. Bringing the data of Annex I, using Mathematica to find the numerical solution of the differential equation in 5400 seconds, obtaining the function of temperature with respect to time, making an image, and the image generated by the calculated value is basically consistent with the image generated by the data provided in Annex II. After data review, heat transfer also includes the invisible effects of various parameters. Radiation heat transfer has the greatest influence on the parameters. There-fore, in the optimization of the model, we mainly optimize the radiant heat parameters based on the multi-layer high-temperature workwear model established by ourselves.

文章引用：高佳丰, 赵之. 多层高温作业服装模型的研究[J]. 建模与仿真, 2019, 8(1): 22-30. https://doi.org/10.12677/MOS.2019.81004

1. 引言

问题的产生

在高温环境下工作时，人们需要穿着专用服装以避免灼伤。专用服装通常由三层织物材料构成，记为I、II、III层，其中I层与外界环境接触，III层与皮肤之间还存在空隙，将此空隙记为IV层。

将体内温度控制在37℃的假人放置在实验室的高温环境中，测量假人皮肤外侧的温度。为了降低研发成本、缩短研发周期，利用数学模型来确定假人皮肤外侧的温度变化情况。

本文以2018年高教社杯全国大学生数学建模竞赛为例，参照赛题所提供的数据集，从以下几个方面对高温作业专用服装设计问题进行探讨：

问题一：专用服装材料的某些参数值已给出，对环境温度为75℃、II层厚度为6 mm、IV层厚度为5 mm、工作时间为90分钟的情形开展实验，测量得到假人皮肤外侧的温度。建立数学模型，计算温度分布，并生成温度分布的Excel文件。

问题二：当环境温度为65℃、IV层的厚度为5.5 mm时，确定II层的最优厚度，确保工作60分钟时，假人皮肤外侧温度不超过47℃，且超过44℃的时间不超过5分钟。

问题三：当环境温度为80℃时，确定II层和IV层的最优厚度，确保工作30分钟时，假人皮肤外侧温度不超过47℃，且超过44℃的时间不超过5分钟。

2. 问题重述

2.1. 背景介绍

在消防、化工、冶金及金属炼钢等行业中，工作人员常处在高温高辐射的环境下工作。在工作时，人们需要穿着高温专用服装以避免灼伤，为了加强对高温专用服装内部热量传递规律的了解，需要建立起织物中包含空气层的多层织物热传递模型，为热防护服的设计提供科学理论依据。

2.2. 提出问题

织物越厚，热阻会相应变大，最长安全工作时间就越长，同时，越厚的织物有更好的储热能力，使得热通量不至于灼伤皮肤。然而过厚的织物，不仅太过沉重，不易穿戴，给高温工作者造成负担，还会增加不必要的经济成本。因此我们应就不同材质的厚度对防热性能进行研究，在满足安全性的前提下，确定材质的最优厚度。

2.3. 研究的意义

通过对热防护服内部热传递规律的深入了解，将为高温作业者避免在高温中的皮肤烧伤提供切实可靠的理论依据。建立起织物中包含空气层的多层织物热传递模型，为高温作业者提供科学有用的安全指导，在满足安全性的前提下，确定材质的最优厚度，有利于降低研发成本、缩短研发周期，提高社会效益。

3. 问题分析

3.1. 问题一的分析

经问题分析，并参考卢琳珍 [1] 等人的热防护服热传递模型，我们建立出多层防护衣模型(如图1)，并采用微分方程法对每层进行分析求解。记每层温度为 $T_{0}, T_{1}, T_{2}, T_{3}, T_{4}$ ，由附件一[3]知每层热传导系数分别为 $k_{1}, k_{2}, k_{3}, k_{4}$ ,每层厚度分别为 $d_{1}, d_{2}, d_{3}, d_{4}$ 。

Figure 1. Multi-layer high temperature work clothes concept map

图1. 多层高温作业服概念图

对附件一[3]内的数据进行差分和柔化，并取前2400秒，如图2，可以明显看出热量传递的速度先逐渐增长，后因为内外温度相近而逐渐降低。

Figure 2. Differential and softening

图2. 差分和柔化数据图

问题一要求我们建立数学模型，计算温度分布。对于问题一，可以求得单位时间单位面积的热传导为： $Q = c ρ d s Δ t$ 。单位时间内每层获得的热量为从前一层获得的热量减去传递给下一层的热量，即： $\frac{d T_{i}}{d t} = \frac{k_{i} (T_{i - 1} - T_{i})}{s d_{i}^{2} c_{i} ρ_{i}} - \frac{d T_{i + 1}}{d t}$ 。将附件一[3]数据带入，可得具体微分方程，用Mathematica在时间t从1秒到5400秒的范围求出上述微分方程的数值解，得到温度 $T_{1}, T_{2}, T_{3}, T_{4}$ 关于时间t的函数以及图像，生成的 $T_{4}$ 图像与附件一[3]中所提供的数据生成的图像基本吻合。

3.2. 问题二的分析

问题二要求我们确定II层的最优厚度，对于问题二，参考巩彦如 [2] 等人的热防护纺织材料隔热性能的数值模拟，把问题二中给定的相关参数带入，将其中的 $d_{2}$ 设为 $d_{2} (t)$ ，则 $d_{2} (t)$ 为常值函数，即 ${d^{'}}_{2} (t) = 0$ ，并将问题中的临界条件 $T_{4} (3300) = 44$ ，加入微分方程组，再次用Mathematica求出关于t从1 s到3600 s的数值解，即可得到 $y (t)$ 的取值。

3.3. 问题三的分析

问题三要求我们确定II层和IV层的最优厚度，对于问题三，将附件一[3]以的参数代入，将其中的 $d_{2}$ 、设为 $d_{2} (t)$ 、 $d_{4} (t)$ ，同时有 ${d^{'}}_{2} (t) = 0$ ， ${d^{'}}_{4} (t) = 0$ ，再加上问题中的临界条件 $T_{4} (1500) = 44$ ， $T_{4} (1800) = 47$ ，可得到具体微分方程，用Mathematica求关于t从1 s到1800 s的数值解，可得到成对的 $d_{2} (t)$ 、 $d_{4} (t)$ 的取值，取其中和最小的厚度为最优厚度。

4. 模型建立、求解与检验

4.1. 问题一的分析、求解与检验

${\begin{cases} \frac{d T_{4}}{d t} = 0.94443 (T_{3} - T_{4}) - 0.94443 (T_{4} - 37) \\ \frac{d T_{3}}{d t} = 0.02712 (T_{2} - T_{3}) - \frac{d T_{4}}{d t} \\ \frac{d T_{2}}{d t} = 0.005677 (T_{1} - T_{2}) - \frac{d T_{3}}{d t} \\ \frac{d T_{1}}{d t} = 0.551386 (75 - T_{1}) - \frac{d T_{2}}{d t} \end{cases}$ (式4.1.1)

将附件一[3]中的参数带入可确定的如上微分方程组，由题意可知，在t = 0秒假人外侧皮肤以及各材质层的温度均为37℃，可得到初值条件：

${\begin{cases} T_{1} (0) = 37 \\ T_{2} (0) = 37 \\ T_{3} (0) = 37 \\ T_{4} (0) = 37 \end{cases}$ (式4.1.2)

用Mathematica可求解出t从1秒到5400秒时的微分方程数值解，详细数值见附件一[3]，可得四层材质的温度时间关系为图3。

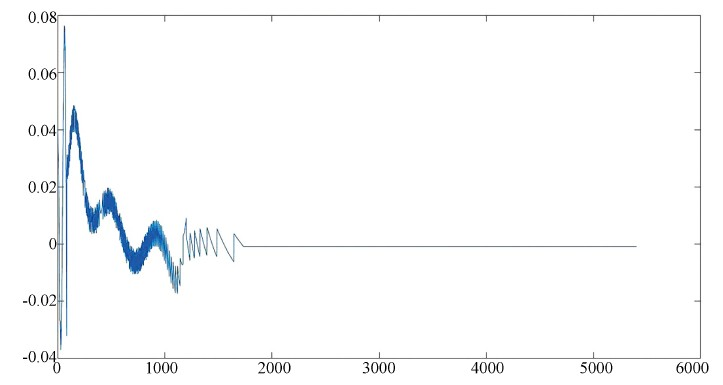
Figure 3. Temperature time relationship of four layers of material

图3. 四层材质的温度时间关系

我们将得到的数据与附件一[3]中给定的数据作差，得到的数据误差极小，最大不超过0.08，如图4所示，模拟效果较好。

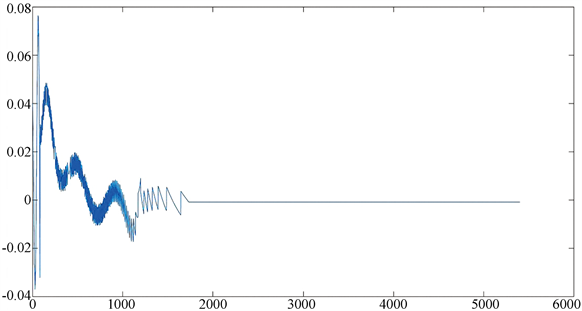
Figure 4. Shows the difference between the data obtained and the given data

图4. 所求得数据与给定数据作差模拟图

4.2. 问题二的分析、求解与检验

$d_{2}$ 在微分方程中作为未知量，设法将 $d_{2}$ 作为一个新的变量添加到微分方程中，则此微分方程将多一个影响T的变量，这样就和偏微分方程一样，为了尽可能增加解题的可行性，提高计算精度，我们将 $d_{2}$ 作为t的函数即 $d_{2} (t)$ ，常数的导数为0可以作为一个微分方程添加到方程组中即 ${d^{'}}_{2} (t) = 0$ ，如果这样将是一个可求的常微分方程组，将附件一[3]与问题二的参数带入也可得到明确的微分方程组：

${\begin{cases} \frac{d T_{4}}{d t} = 0.78052 (T_{3} - T_{4}) - 0.78052 (T_{4} - 37) \\ \frac{d T_{3}}{d t} = 0.02712 (T_{2} - T_{3}) - \frac{d T_{4}}{d t} \\ \frac{d T_{2}}{d t} = 2.04397 \times 10^{- 7} / (T_{1} - T_{2}) d_{2}^{2} (t) - \frac{d T_{3}}{d t} \\ {d^{'}}_{2} (t) = 0 \end{cases}$ (式4.2.1)

利用问题二的叙述以及模型的假设得到初值条件：

${\begin{cases} T_{4} (3300) = 44 \\ T_{4} (3600) = 47 \\ T_{4} (0) = 37 \\ T_{3} (0) = 37 \\ T_{2} (0) = 37 \\ T_{1} (0) = 37 \end{cases}$ (式4.2.2)

再次用Mathematica求出关于t从1秒到3600秒的数值解，即可得到 $d_{2}$ 的取值为16.89 mm，图5为相应的四层材质温度随时间增长的模拟图像。为了使材质二、三层温度时间曲线较为分明，图6为时间为1秒~1600秒的温度时间图像。

Figure 5. Simulation image of four-layer material temperature increasing with time

图5. 四层材质温度随时间增长的模拟图像

Figure 6. Simulation image of four-layer material temperature increasing with time (1 s - 1600 s)

图6. 四层材质温度随时间增长的模拟图像(1 s~1600 s)

4.3. 问题三的分析、求解与检验

如上述问题二，我们没有必要再引入一个新变量 $d_{4}$ 来增加我们计算的负担，与问题二中计算方法相似我们将常数 $d_{4}$ 作为关于t的函数即 $d_{4} (t)$ ，将问题三和附件一[3]中的参数带入，可得明确的微分方程组：

${\begin{cases} \frac{d T_{4}}{d t} = 2.3611 \times 10^{- 5} (T_{3} - T_{4}) / d_{4}^{2} (t) - 2.3611 \times 10^{- 5} (T_{4} - 37) / d_{4}^{2} (t) \\ \frac{d T_{3}}{d t} = 0.02712 (T_{2} - T_{3}) - \frac{d T_{4}}{d t} \\ \frac{d T_{2}}{d t} = 2.04397 \times 10^{- 7} / d_{2}^{2} (t) (T_{1} - T_{2}) - \frac{d T_{3}}{d t} \\ \frac{d T_{1}}{d t} = 0.551386 (65 - T_{1}) - \frac{d T_{2}}{d t} \\ {d^{'}}_{2} (t) = 0 \\ {d^{'}}_{4} (t) = 0 \end{cases}$ (式4.3.1)

初值条件类似如上：

${\begin{cases} T_{4} (1500) = 44 \\ T_{4} (1800) = 47 \\ T_{1} (0) = 0 \\ T_{2} (0) = 0 \\ T_{3} (0) = 0 \\ T_{4} (0) = 0 \\ T_{5} (0) = 0 \end{cases}$ (式4.3.2)

我们同样利用mathmatic软件求出在t从1秒到1800秒的数值解， $d_{2} = 12.24 mm$ ， $d_{4} = 6.4 mm$ ，并得到图像如图7：

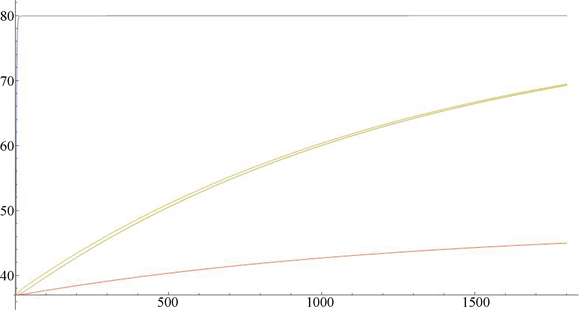
Figure 7. Numerical solution (1 s - 1800 s)

图7. 数值解(1 s~1800 s)

5. 模型推广与改进

5.1. 实例应用

我们建立的包含空气层的多层织物热传递模型，加强了对高温专用服装内部热量传递规律的了解，不仅适用于高温的工作环境中，同样适用于经常接触高电压、高辐射、低温的环境之中，为防护服的设计提供科学理论依据。

5.2. 模型改进

经资料检阅，热传导还包括着各种参数的隐形影响。其中辐射传热对参数影响最大。所以在模型的优化上，我们主要在自身建立的多层高温作业服模型的基础上，加进对辐射热参数的优化。

( $ρ_{i}$ 为密度， $c_{i}$ 为对应比热， $k_{i}$ 为对应传导率， $F_{x}$ 为向左向右辐射量)

注：t取值在5400秒内，x按厚度分层取值。

经资料检阅，热辐射量满足：

${\begin{cases} \frac{\partial F_{1}}{\partial x} = β F_{1} - β σ T^{4} \\ \frac{\partial F_{2}}{\partial x} = β F_{2} - β σ T^{4} \end{cases}$ (式5.2.1)

$β$ 为辐射吸收常数单位； $σ$ 为斯蒂芬-波尔兹曼常数，

采用有限差分法来解决以多层热防护服、空气层为整体的偏微分方程组。辐射项的边界条件和随温度变化的对流系数的存在，造成了偏微分方程组的非线性，所以我们可以采用显隐式方法来解决这个问题。具体计算方法如下：

${\begin{cases} c ρ \frac{\partial T}{\partial t} = \frac{\partial}{\partial x} (k \frac{\partial}{\partial x}) + θ (x, t) \\ T (x, 0) = T_{1} (0) \\ - {k \frac{\partial T}{\partial t} |}_{x = 0} = {(q_{c o n v} + q_{r a d}) |}_{x = 0} \end{cases}$ (式5.2.2)

将外壳和左边界离散，隐式迭代最终得：

外壳公式： $- S_{1} T_{i - 1}^{j + 1} + [1 + S_{1} + S_{2}] T_{i}^{j + 1} - S_{2} T_{i + 1}^{j + 1} = T_{i}^{j} + r θ_{i}^{j}$

左边界公式： $- k \frac{T_{1}^{j + 1} - T_{0}^{j + 1}}{h} = h_{c, 0} (T_{g} - T_{0}^{j + 1})$

改进模型优点：可以看出改进模型更加精准，与实况模型更加贴切。

6. 模型评价

模型优点

1) 对建立的高温作业服模型进行仿真的结果与附件一[3]提供的现实数据相符合，说明了热传递模型的合理性。

2) 应用该模型预测仿真了织物层随时间的变化规律，便于观察分析。

3) 通过该模型可以确定每层的最优厚度，预测最长的安全工作时间，为热防护服的设计提供了科学理论依据。

4) 在进行模拟仿真的时候，将一维模型推广到三维模型，更符合实际情况。

5) 对模型进行了优化，由常微分计算后，在其基础上利用更加准确的偏微分进行了改进，与附件一[3]所提供的数据基本一致，相互吻合，更加确切地说明了该模型的合理性。

6) 建立该模型时，详尽地考虑了各种可能性，在大量的物理原理基础上，使整个模型的构建更加符合现实世界，更具有科学性。

7) 采用计算机计算大量数据，并绘制大量模拟图，清晰明了，省时省力。

8) 可以看出改进模型考虑到了热传导在双向辐射下的影响，与物理现象更加贴切，并且经过资料查阅，我们在常微分方程的基础上采用偏微分方程，使整个模型更加趋于精准，计算主要利用Comsol软件的有限元分析模块，采用大量数据进行计算，与实况模型更加符合。

附录

2018年全国大学生数学建模竞赛A题附件一[3]数见：

http://www.mcm.edu.cn/html_cn/node/7cec7725b9a0ea07b4dfd175e8042c33.html

参考文献

[1]	卢琳珍, 徐定华, 徐映红. 应用三层热防护服热传递改进模型的皮肤烧伤度预测[J]. 纺织学报, 2018, 39(1): 111-119.
[2]	巩彦如, 张璇, 毛志平, 王新厚. 热防护纺织材料隔热性能的数值模拟[J]. 东华大学学报(自然科学版), 2010, 36(2): 115-117.

为你推荐

友情链接