1. 引言
本文考虑如下的无约束问题:
(1)
其中
是连续可微函数。
BFGS方法是求解无约束优化问题的一种非常有效的拟牛顿方法,BFGS方法在Wolfe搜索下对求解凸优化问题具有全局收敛性,但对非凸问题不一定收敛。在文献 [1] 中刘陶文提出了一种扰动的BFGS方法,其中对标准的BFGS方法的迭代矩阵进行了扰动,该方法证明了在Wolfe搜索下对求解非凸问题具有全局收敛性。Zhang,Deng和Chen在文献 [2] 中基于新的拟牛顿矩阵提出了一种新的拟牛顿算法,该方法满足更好的割线方程。本文的目的就是基于文献 [1] 的扰动思想,同时结合文献 [2] 中的BFGS迭代公式,提出了一种新的扰动的BFGS方法。
本文安排如下,在第二节中我们提出新的扰动BFGS方法的算法,在第三节中我们分析了该算法的全局收敛性,第四节中我们进行了数值实验,验证了该算法的有效性,在第五节中我们对论文进行了总结。
2. 算法
求解问题(1)新的扰动BFGS方法基本的迭代格式为
(2)
其中
是当前的近似解,
为搜索方向,
是步长。
基于文献 [1] 的扰动思想,通过求解下列线性方程组得到搜索方向
(3)
其中
表示其梯度,
为拟牛顿矩阵,也就是
在点x处的Hessian矩阵的近似,并且它要求是正定的。Q是某个给定的对称正定矩阵,
且它的值依赖于k,依照某种规则取值为
或者
,其中
是某一个参数且它的值与k有关,当
时,
。
步长
是采用Wolfe型非精确搜索确定的,即通过求解
(4)
来计算步长
,则条件
被满足,其中
和
是正的常数,且满足
。
新的拟牛顿矩阵由Zhang,Deng和Chen文献 [2] 提出,由下列BFGS公式得到
(5)
其中
(6)
(7)
(8)
再由Wolfe搜索下则条件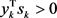 被满足,而由Zhang,Deng和Chen文献 [2] 中的引理4可知当
,
。
被满足,而由Zhang,Deng和Chen文献 [2] 中的引理4可知当
,
。
下面我们给出求解问题(1)的新的扰动的BFGS方法的具体步骤:
算法1.1:(新的扰动的BFGS方法)
步0:选择初始点
和初始的对称正定矩阵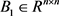 以及
以及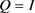 。选用常数
,
,
,
,
以及
。令
以及
。令
。
。选用常数
,
,
,
,
以及
。令
以及
。令
。
步1:解线性方程组(3)得到
,转步2。
步2:由条件(4)来计算
,令
。
步3:由修正公式(5),(6),(7),(8)确定
。
步4:如果
,令
,
,
。
否则令
以及
其中
。
步5:令
,然后转步1。
在算法1.1中
按下面的规则逐步被减少:
其中
,
是正的常数,并且
,i取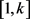 中的某个指标,它的值随着迭代过程被不断的修改,这样得到一个序列
中的一个公比不超过
的几何子列。如果
中的某个指标,它的值随着迭代过程被不断的修改,这样得到一个序列
中的一个公比不超过
的几何子列。如果
成立,则
单调非增并且当
时
。由此可以得到当
有界时,
。
3. 算法全局收敛性证明
为了证明新的扰动BFGS方法的全局收敛性,我们做出如下的假设
假设3.1:水平集
有界,函数
在
上Lipschitz连续的梯度,即存在常数
满足
(3.1)
需要注意的是采用线性搜索(4),由(5)产生的矩阵总是正定的,从而序列
是单调递减的,而且由线性搜索(4)的第一个不等式以及假设3.1可以得到
由此可推出
(9)
为了表示的方便,根据算法1.1中的步4我们定义指标集合
(10)
以及
(11)
为了证明算法1.1的全局收敛性我们需要先证明如下的引理:
引理3.1:假设
是有限集,则算法1.1产生的序列
有非零的下界,并且当
时,
。
证明:如果
是有限集,因此
被减少有限次,也就是说存在一个整数
使得对所有的
有
,由于
是正定的,对于所有的k有
(12)
由(4)中的第二个不等式以及假设3.1,我们得到对所有的
,不等式
成立。因此,由(12),我们可以推出
(13)
而且由(13),(9)和(12)易知当
时,
。
引理3.2:如果
是无限集,而
是有限集,则
必有
. (14)
证明:令
,
。则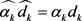 。当
是有限集时,我们从集合
的定义(11)以及算法1.1的步4知,对于任何的
且
。当
是有限集时,我们从集合
的定义(11)以及算法1.1的步4知,对于任何的
且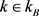 有,
。即
有,
。即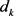 满足:
满足:
所以
(15)
再由(4)的第二个不等式和
的Lipschitz连续性得
由上面不等式以及(15)可推出
进而由上面的关系以及(15)和(9),我们得
(16)
而且对所有的
,有
因而由(16)可得(14)。
引理3.3:如果
是有限集且
也是有限的,那么(14)成立。
证明:我们用反证法假设存在一个某个正数
使得对所有k有
成立。由算法的1.1的步4可得,当
时,
,并且
(17)
当
是有限集时,则(12)对所有的
成立。由引理3.1以及(9)可得
。由(3)和(17)可推出,对所有
有下面的不等式成立
这就意味着
这与假设相矛盾,所以必有(14)成立。
在引理3.2和3.3的基础上我们证明了算法1.1的全局收敛性。
定理3.1:设序列
由算法1.1产生并且满足假设3.1则(14)成立。
证明:我们考虑两种情形:(i)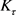 是无限集和(ii)
是有限集。
是无限集和(ii)
是有限集。
情形(i):由
的定义(10),必存在
中的一个公比不超过
几何子序列,此时必有(14)成立。
情形(ii):我们需要考虑
是无限还是有限两种情况。由引理3.2和3.3可知,上面两种情况的任意一种情况中,(14)总是成立的,也就是说
被减少无穷多次,由
的定义(10)中可知情形(ii)是不会出现的。
由定理3.1的证明可以看出,
一定被减少无穷多次,所以当
时,
。如果
是有界的,那么当k充分大时,
,并且当
时,
。
4. 数值实验与结果分析
在CPU为1.6 HZ、内存为512 MB的电脑上分别对新的扰动的BFGS算法(算法1.1)和文献 [3] 中的CBFGS等算法进行了数值实验,其中测试问题的函数都来源于文献 [4] 。程序采用Matlab语言编写,在算法中我们使用
作为算法的终止条件,算法中有关常数与参数的选择如下:
,
,
,
,
,
,
(单位矩阵)。
首先选择了3个二维问题,1个三维问题,2个四维问题,对算法进行了分析,问题分别是:
rose
初始点:
,精确解:
,
。
badscp
初始点:
,精确解:
,
。
badscb
初始点:
,精确解:
,
。
helix
其中
,
,
初始点:
,精确解:
,
。
sing
初始点:
,精确解:
,
。
wood
初始点:
,精确解
,
。
通过编程计算得到表1。

Table 1. Result analysis of solving several kinds of problems
表1. 求解几类问题的结果分析
通过表1的结果,得出我们的算法能有效地解决二维和三维问题,以及四维问题,说明我们的算法是有效的。

Table 2. Comparisons with other methods
表2. 与其他几类方法的比较分析
通过表2对不同的BFGS方法的迭代步进行分析,我们可以得出我们扰动的算法在求解badscp问题时需要188步,比其他三种方法的迭代步要少,同时在求解其他问题时的迭代步骤相差不大。
5. 小结
通过数值实验结果和全局收敛性的证明,说明我们提出的新扰动的BFGS方法对求解非凸优化问题是有效的。
参考文献