1. 引言
在本文中,所有的图都是无向、有限的简单图。对于在本文中没有提到的图论的概念与术语,我们可以参考 [1] 。
设图G是一个连通图,S是图G中至少有2个顶点的集合,T是G的一棵子树。如果
,则称T是G的一棵S-斯坦纳树。设
与
是S-斯坦纳树,如果
且
,则称
与
是内部不交的S-斯坦纳树。对于
的一个子集S,
表示图G中内部不交的S-斯坦纳树的最大数目。如果
,则
是局部点连通度。对于
的整数,
是当S遍及
的所有k元子集时的最小的
,称它为广义k-连通度,简称
-连通度。Chartrand等人 [2] 引入了
-连通度。显然,当
时,
。
笛卡尔积是最重要的图运算之一,并且在网络的设计与分析中有重要作用。在过去的几十年,许多图论学者研究了笛卡尔积图的(边)连通度 [3] - [9] 。显然,在同构意义下,该运算满足交换律,即
,该运算满足结合律,即
。
对于一般图G来说,确定
是一件非常困难的事情。到目前为止,只有少数图类的
-连通度被确定,例如,Chartrand等人 [10] 确定了完全图的
-连通度;Lin和Zhang确定了超立方体的
-连通度;Li和Wang [11] 确定了递归循环图的
-连通度与
-连通度,等等。图论学者研究了图的广义连通度的上界与下界 [12] [13] [14] [15] [16] ,图论学者研究了图运算的广义(边)连通度的上界与下界 [12] [17] 。更多的结果,可以参考 [18] 。
在本文中,我们将研究完全图的笛卡尔积的
-连通度。本文的结构如下,在第2部分,我们将介绍一些定义和已知的结论;在第3部分,我们将给出主要的结果。
2. 预备知识
设G和H是两个图,图G与H的笛卡尔积,记作
,其顶点集为
,两个顶点
与
相邻当且仅当
且
,或
且
。特别地,n条路的笛卡尔积是n-维网格图。长为1的n条路的笛卡尔积是n-维超立方体。
设G与H是两个图,顶点集分别为
,
。我们用
来表示
的子图,这个子图是由顶点集
诱导出来的。类似的,我们用
来表示
的子图,这个子图是由顶点集
诱导出来的。显然,对于图G中的不同顶点
与
,有
。为了简单,我们可以用
来代替
。类似的,我们也可以用
来代替
。下面的几个符号可以简化我们的证明。
给定一个顶点
,对于
中的任意顶点u,有
,对于G中的任意子图
,有
,其中
,
。
给定一个顶点
,对于任意顶点
,有
,对于任意子图
,有
,其中
,
。
类似的,给定一个顶点
,对于
可以定义映射
,对于
可以定义映射
;给定一个顶点
,对于
可以定义映射
,对于
可以定义映射
。
下面的几个定理和引理对我们要证明的结果很重要。
定理2.1 [10] :对于任意两个整数n和k,
,有
。
引理2.2 [13] :设图G是一个至少有3个顶点的连通图,如果图G有两个最小度为
的相邻顶点,则有
;而且,上界是紧的。
定理2.3 [1] :设图G是一个k-连通图,如果x与y是G中的一对不同顶点,那么在图G中存在k条内部不交的xy-路
。
引理2.4 [19] :如果图G是k-连通的,那么对于任意顶点x和子集
,满足
,都有一个大小为k的x,U-扇。
定理2.5 [20] :
,
。
引理2.6 [20] :设
是两个整数,
,G是一个r-正则图,如果
,那么
。
引理2.7 [17] :设
是k个圈,则
。
3. 主要定理及其证明
在本文中,
表示有
个顶点的完全图,其中
。一条xy-路是一条起始于x,终止于y的路。对于一条路P来说,其中
,我们用
去表示P上连接
的子路。
定理3.1:对于任意两个完全图
与
,有
。
证明:根据
与
的取值情况,考虑如下三种情形。
情形1:
。
因为
,所以两个完全图都是
。显然,
。
情形2:
。
由引理2.2知,
,故只需证
。令
,
,
。下面分两种子情形讨论。
子情形2.1:
,
。
不失一般性,假设
。由定理2.1知,
,故在
中有
棵内部不交的S-斯坦纳树,记作
。令
。显然,
是
棵内部不交的S-斯坦纳树。
子情形2.2:S中的某两个顶点属于某个
,
。
不失一般性,假设
,
。因为
,
,
,所以由定理2.3知,在
中存在
条内部不交的xy-路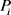 ,
,在
中存在
条内部不交的
-路
,
。令
是在
上的x的邻点。令
,
。显然,
是
棵内部不交的S-斯坦纳树。
,
,在
中存在
条内部不交的
-路
,
。令
是在
上的x的邻点。令
,
。显然,
是
棵内部不交的S-斯坦纳树。
情形3:
。
由引理2.2知,
,故只需证
。令
,
,
。下面分三种子情形讨论。
子情形3.1:
,
。
因为此情形与子情形2.1的讨论类似,所以留给读者证明。
子情形3.2:S中的某两个顶点属于某个
,
。
因为此情形与子情形2.2的讨论类似,所以留给读者证明。
子情形3.3:S中的三个顶点分别属于不同的
,
。
不失一般性,设
,
,
。下面分三种情形讨论。
如果
,不妨设
。由定理2.1知,
,所以在
中有
棵内部不交的S-斯坦纳树,记作
。令
,
。显然,
是
棵内部不交的S-斯坦纳树。
如果
,
, 其中
。因为
,
,所以由定理2.3知,在
中存在
条内部不交的
-路
,
。因为
是简单图,所以在
中可以找到
条长度至少为2的
-路
,
。令
是在
上的x的邻点,
,
;
;
;
,
。显然,
是
棵内部不交的S-斯坦纳树。
如果
,
,
,其中
不相等。当
时,由引理2.7知,
,故定理成立。当
和
时,令
是在图
中除顶点
与
外的x的邻点,则
,
。令
;
;
;
,
。显然,
是
棵内部不交的S-斯坦纳树。
定理3.2:对于任意
个完全图,有
。
证明:对k用归纳法。因为图的笛卡尔积满足交换律和结合律,所以可设
。如果
,那么
是超立方体
,由定理2.5与引理2.6知,定理成立。
接下来只讨论
即可。当
时,由定理3.1知,定理成立;假设对于任意不超过
个完全图的笛卡尔积,定理都成立,即
成立;现在证明对于任意k个完全图的笛卡尔积,定理成立。由引理2.2知,
,故只需证
。为了简便,令图G表示图
,
,
。令
,
,
。考虑如下三种情形。
情形1:
,
。
不失一般性,假设
。由归纳假设知,在
中可以找到a棵内部不交的S-斯坦纳树,记作
。我们只需在
外找
棵内部不交的S-斯坦纳树,令
,
。显然,
是b棵内部不交的S-斯坦纳树。
情形2:S中的某两个顶点属于某个
,
。
不失一般性,假设
,
。下面分两种子情形讨论。
子情形2.1:
。
因为
,
,
,所以由定理2.3知,在
中存在
条内部不交的xy-路
,
,在
中存在
条内部不交的
-路
,
。令
是在
上的x的邻点。在
中任取一棵
-斯坦纳树
,
。令
,
;
,
。显然,
是b棵内部不交的S-斯坦纳树。
子情形2.2:
。
不失一般性,假设
。因为
,
,所以由定理2.3知,在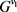 中存在
条内部不交的xy-路
,
。令
是在
上的x的邻点。令
,
;
,
。显然,
是b棵内部不交的S-斯坦纳树。
中存在
条内部不交的xy-路
,
。令
是在
上的x的邻点。令
,
;
,
。显然,
是b棵内部不交的S-斯坦纳树。
情形3:S中的三个顶点分别属于不同的
,
。
不失一般性,假设
,
,
。下面分三种子情形讨论。
子情形3.1:
,
。
不失一般性,假设
。因为
,所以在
中,顶点x有
个邻点,记作
。令
,
。又因为
是完全图,所以由定理2.1知,
,故在
中有
棵内部不交的S-斯坦纳树,记作
。显然,
是b棵内部不交的S-斯坦纳树。
子情形3.2:
,
,
。
因为
,
,所以由定理2.3知,在
中存在
条内部不交的
-路
,
。因为图G是简单图,所以在
中可以找到a条长度至少为2的
-路
,
。令
是在
上的x的邻点。令
,
;
;
;
,
。显然,
是b棵内部不交的S-斯坦纳树。
子情形3.3:
,
,
,其中
不相等。
令
,
。考虑如下两种情况。
如果在G中,
中的某两个顶点不相邻。不失一般性,假设在G中
不相邻。因为
,所以在G中存在
条内部不交的
-路,记作
,设
是
的邻点,
。假设
不在
上,
。由引理2.4知,在G中存在一个从
到
的
-扇,记作
,其中有一条
-路,
,
是一条
-路。令
,
。因为每个
有一棵支撑树
,
,所以我们找到a棵内部不交的S-斯坦纳树,记作
。因为
是
-连通的,所以在
中存在
条内部不交的
-路,记作
,设
是
的邻点,
。又因为
是完全图,所以可假设
,令
,
,故
,
。
因为
,所以在
中存在一个从
到
的
-扇,记作
,其中有一条
-路,
,有一条
-路
。令
,
;
;
。显然,
是b棵内部不交的S-斯坦纳树(如图1所示)。

Figure 1. Solid lines in bold for
,
; Solid lines for
,
; Dashed lines for
; Dashed lines in bold for
图1. 粗实线表示
,
;细实线表示
,
;细虚线表示
;粗虚线表示
如果在G中,
两两相邻。由引理2.7知,在
中有3条内部不交的S-斯坦纳树,记作
。因为G是
-连通的,所以
,故在
中存在
条内部不交的
-路,记作
。令
是
的邻点,
。由引理2.4知,在
中存在一个从
到
的
-扇。类似于情况1,可以构造
棵内部不交的S-斯坦纳树
。又因为
,所以可以构造
棵内部不交的S-斯坦纳树
。显然,
是b棵内部不交的S-斯坦纳树。
基金项目
国家自然科学基金(No. 11401181)。
致谢
作者非常感谢审稿人和编辑的宝贵意见和建议,改善了本文的呈现。