基于邻域相似性的空谱联合稀疏表示的高光谱图像分类

Hyperspectral Image Classification Based on Neighborhood Similarity and Spatial Spectral Joint Sparse Representation

摘要: 传统的稀疏表示分类方法仅考虑图像数据的稀疏特性，并未利用邻域像元间的相似性与独特性，因此提出一种基于邻域相似性的空谱联合稀疏表示的分类方法来提高高光谱图像分类精度。该方法将像元间的稀疏特性和邻域信息结合起来，利用像元间的空间距离权重与光谱距离权重度量待测中心像元Y与邻域像元的相似性，即计算邻域权重，设定相似度阈值，选取与像元Y相似度高的像元从而得到最优邻域窗口，最后通过联合稀疏表示来确定像元Y的类别。实验结果表明，该方法能够有效提高分类精度，且在不同实验数据下具备良好的稳定性。

Abstract: The traditional sparse representation classification method only takes into account the sparsity of image data, and does not make use of the similarity and uniqueness between neighboring pixels. Therefore, a new method based on neighborhood similarity and spatial spectral joint sparse representation is proposed to improve the classification accuracy of hyperspectral image. The method combines pixel sparse features with neighborhood information, and uses the weight of spatial distance and spectral distance weight between pixels to measure the similarity between the center pixel Y and neighboring pixels, namely, calculate neighborhood weights, set similarity thresholds, select pixels with high similarity to pixel Y, and get the optimal neighborhood window. Finally, a class of pixel Y is determined by joint sparse representation. Experimental results show that this method can effectively improve classification accuracy and has good stability under different experimental data.

1. 引言

随着光谱成像技术的日趋成熟，高光谱遥感在理论上、技术上、应用上发生了显著的变化 [1] 。高光谱图像(Hyperspectral Image, HSI) [2] 中的每个像素由其对应的各种光谱带响应的矢量来表示，不同的材料在特定的波长下通常会反射不同的电磁能量。HSI最重要的应用之一是图像分类 [3] ，现有的分类方法有人工神经网络(Artificial Neural Network, ANN)、支持向量机(Support Vector Machine, SVM)、最近邻(Nearest Neighbor, NN)分类等。近年来，基于稀疏表示(Sparse Representation, SR)的分类方法越来越多地被应用于高光谱图像的分类，文献 [4] 提出了一种基于类别关系的稀疏表示分类方法，该方法将像元间的相关性和欧式距离关系有效结合，提高地物分类效果。文献 [5] 在联合稀疏表示之前加入高光谱图像的主成分分析，提取其形态学特征，进而对局部空间区域新特征像元进行联合稀疏表示，提高了分类精度。文献 [6] 提出了一种残差融合分类方法，该算法有效利用图像数据的光谱信息和空间信息。文献 [7] 提出了一种融合稀疏表示和协同表示的分类算法，该算法通过融合残差值大小确定地物类别。

为提高高光谱图像的分类精度，有效融合邻域像元间的相似性与独特性，本文提出一种基于邻域相似性的空谱联合稀疏表示的分类方法。

2. 联合稀疏表示算法模型

稀疏表示分类(Sparse Representation Classification, SRC)方法中每个像元都用稀疏向量表示，计算像元和各类训练样本的最小残差，确定待测像元类别。在高光谱图像中，相邻的像元极有可能属于同一类地物 [8] ，因此可以加入空间邻域信息，使邻域内的所有像元共用同一个稀疏表示模型，即联合稀疏表示模型。该模型中待测像元的类别由待测像元及邻域内其他像元共同决定。假设高光谱图像中有C类不同

的地物，每类均有n个训练样本，则由所有训练样本构成的字典可以表示为 $A=\left[A_1,A_2,\cdots ,A_C\right]$ ，其中，A_C为第C类字典。待测中心像元与其邻域像元可以表示为 $Y=\left[y_1,y_2,\cdots ,y_T\right]$ ，其中，T为邻域；y₁为待测中心像元；其余像元为y₁的邻域像元。因此在联合稀疏表示模型中，Y可以表示为：

$Y=\left[A{\alpha }_1，A{\alpha }_2，\cdots ,A{\alpha }_t\right]=AS$ (1)

式中， $S=\left[{\alpha }_1,{\alpha }_2,\cdots ,{\alpha }_T\right]$ 为稀疏矩阵， ${\alpha }_i$ 为S中第i个像元的稀疏向量( $i=1,2,\cdots ,T$ )。则稀疏矩阵S可通过如下联合稀疏重构模型求得：

$\hat{S}=\arg \underset{s}{\min }\left|\right|AS-Y|{|}_F,s.t.|\left|S\right|{|}_{row,0}\le K$ (2)

式中， ${\Vert ·\Vert }_F$ 表示取F范数； ${\Vert S\Vert }_{row,0}$ 表示稀疏矩阵中非零行的个数，K为稀疏度。求得稀疏系数矩阵S后，待测中心像元便可以根据重构残差被区分出来，其表达式为

$class\left(y\right)=\arg \underset{c=1,2,\cdots ,C}{\min }{r}_C\left(Y\right)$ (3)

式中， $r_c\left(Y\right)={\Vert Y-A_C{\hat{S}}_C\Vert }_F$ 为第c类残差， $A_C$ 为第c类训练样本组成的字典， ${\hat{S}}_C$ 表示第c类字典对应的重构系数。

3. 基于邻域相似度的空谱联合稀疏表示的分类方法

在实际的地物情况中，邻域内的地物往往存在多种类别，若在地物种类复杂区域直接进行联合稀疏表示，分错的概率很高。光谱相似性测度是高光谱影像分类和信息提取的基础，光谱匹配模型即是通过将像元光谱与参考光谱的比较，求算光谱向量之间的相似性或差异性，以有效提取光谱维信息，对地物性质进行详细的分析。为提升地物分类性能，充分利用邻域间像元间的相似性与独特性，本文提出在待测像元的邻域内的所有像元中，选择与待测像元相似性高的像元，构建最优邻域窗口，再利用JSR模型分析待测像元的地物类别。

高光谱图像包含了丰富的光谱信息，且不同类别的地物对各个波段的光谱响应不同。几何空间匹配方法是一种较为成熟的光谱相似性度量算法，其将光谱向量看成高维特征空间中的一个点，则两条光谱曲线之间的相似性可以用二者的空间距离来表示。兰氏距离可以有效的计算两个样本集的相似程度，同

时也可以用来比较两个向量的相似度。因此可以将像元光谱向量间的兰氏距离作为空间距离权重 $G_{y_1,y_i}$ ，对于待测像元 $y_1$ 的像元集 $Y=\left[y_1,y_2,\cdots ,y_T\right]$ ，两个像元y₁，y_i之间的空间距离权重为：

$G_{y_1,y_i}=\exp \left(-L\left(y_1,y_i\right)\right)$ (4)

$L\left(y_1,y_i\right)$ 为像元y₁，y_i之间的兰氏距离，定义为：

$L\left(y_1,y_i\right)=\frac{1}{b}{\displaystyle \underset{j=1}{\overset{b}{\sum }}\frac{\left|y_{1_j}-y_{i_j}\right|}{y_{1_j}+y_{i_j}}}$ (5)

式中， $y_{1j}$ 和 $y_{ij}$ 分别是待测中心像元光谱和邻域像元光谱第j波段的光谱值，b为波段数。空间距离权重和距离度量相反，距离越小，空间距离权重越大，距离越大，空间距离权重越小。

在高光谱图像中，由于每种地物边界部分均可能存在多种混合地物，若仅仅利用兰氏距离作为邻域

相似度判别的唯一标准，极大可能造成类别的错分。针对以上问题本文引入光谱距离权重 $A_{y_1,y_i}$ 来平衡像元的稀疏相似性和邻域相似性，其表达式为：

$A_{y_1,y_i}=\exp \left(-\frac{{\Vert y_1-y_i\Vert }_2^2}{2{\mu }_s^2}\right)$ (6)

式中，A_y1,yi表示待测中心像元与邻域像元的光谱相似权重；y₁、y_i、μ_s分别表示待测中心像元的光谱值、邻域像元的光谱值以及光谱标准差；μ_s由文献 [9] 得知为3500。

为了同时利用图像数据稀疏特性和邻域信息，提升各类地物的区分性，本文将光谱距离权重引入空谱联合稀疏表示图像分类理论中，利用计算光谱距离权重获取相邻像素的相似度，剥离相似度较低的邻域像素，将剩余像素应用于空谱联合稀疏表示模型进行高光谱影像分类。空间距离权重与光谱距离权重相结合并用于度量待测中心像元与邻域像元的相似性，即计算邻域权重W_y1,yi，其表达式为：

$W=\lambda \ast G_{y_1,y_i}\ast A_{y_1,y_i}$ (7)

式中，λ为比重参数，用来平衡空间距离权重和光谱距离权重。设定相似度阈值τ，当权重W_y1,yi大于τ时，像元的光谱相似度较高，尤其对于边界区域的像元，其邻域内的像元类别复杂。JSRC算法假定邻域内各像元对中心像元的影响权重相同，在分类时必定对分类结果产生影响，因此选择邻域内与中心像元相似度高的像元就显得尤为重要。

由于邻域像元距离待测中心像元越近，属于同一地物的可能性就越大，即权重W_y1,yi越大，因此，当邻域范围达到一定范围时，距离待测像元越远的邻域像元与待测像元基本不属于同一地物，基于高光谱图像的这一特性，考虑到时间复杂度以及数据集上地物的分布特点，在计算最优邻域前将所有待测像元的邻域大小均设置为15 × 15。通过式(4)~式(7)可以计算得到权重W_y1,yi，从而得到每个待测中心像元的最优邻域T，求每个待测中心像元最优邻域的基本流程如图1所示。

Figure 1. Obtaining the best neighbor window flow chart

图1. 求取最优邻域窗口流程图

由图1可知，此算法不同于JSRC分类算法以待测像元为中心的取周围的n × n像元作为邻域窗口大小，而是通过空谱相结合算法计算每个待测中心像元的邻域像元权重来选择邻域窗口。根据以上权重公式计算得到的每个待测中心像元与邻域像元的权重W_y1,yi的大小来选择最优邻域T的大小，最终通过联合稀疏表示模型计算出如下所示的重构残差来得出待测中心像元y为

$class\left(y\right)=\arg \underset{c=1,2,\cdots ,C}{\min }{r}_C\left(Y\right)={\Vert YW-A_C{\hat{S}}_C\Vert }_2$ (8)

通过此算法计算每个待测中心像元的邻域像元权重来选取的邻域窗口是不规则且大小不同的窗口，并且每个邻域窗口都是此算法下的最优邻域。基于邻域相似性的空谱联合稀疏表示的分类算法(WJSRC)步骤如下：

输入 在图像中每个类别中随机选取一定数量的像元作为训练样本构成结构化字典 $A=\left[A_1,A_2,\cdots ,A_C\right]$

输出 测试样本的类别

初始化 初始化归一化字典A

循环 对于高光谱图像中的每一个像元y

1)计算邻域权重W_y1,yi，其中n = 15 × 15，并选取邻域权重W_y1,yi中大于τ的邻域像元为最优邻域窗口T；

2)构建联合信号矩阵 $Y=\left[y_1,y_2,\cdots ,y_T\right]\in R^{B\times T}$ ，并且归一化联合信号矩阵Y；

3) 通过式(2)计算得到稀疏矩阵S；

4) 通过式(8)计算残差 $r_C\left(Y\right)$ ，得到测试样本y的类别；

结束

4. 实验及结果分析

4.1. 实验数据集

实验中使用Indian Pines高光谱遥感数据集和Pavia University高光谱遥感数据集进行验证。

Indian Pines数据集：该数据集是由AVIRIS传感器获得的，共有220个波段，图像大小为145 × 145，包含16个地面真理类，如图2(a)所示。在实验中，通过去除20个吸水带，波段数减少到200。对于每一类，随机选择约10%的标记样本进行训练，并使用剩余的90%进行测试，如表1所示。

(a) (b)

Figure 2. (a) Indian Pines hyperspectral imaging; (b) Pavia University hyperspectral imaging

图2. (a) Indian Pines高光谱影像；(b) Pavia University高光谱影像

Table 1. 16 Ground-Truth classes in Indian Pines

表1. Indian Pines图像中的16个真实类

Pavia University数据集：Pavia University图像是在2001年通过ROSIS传感器获得的，图像大小为610 × 340个像素，共有115个波段，除去其中水吸收和噪声波段去掉，剩下其中103个波段，该图像总共包含9个类别地物分别为：沥青(Asphalt)，草地(Meadows)，砾石(Gravel)，树(Trees)，金属板材(Painted metal sheets)，裸露土壤(Bare Soil)，柏油屋顶(Bitumen)，自挡砖(Self-Blocking Bricks)，阴影(Shadows)，如图2(b)所示。对于每一类，随机选择约10%的标记样本进行训练，并使用剩余的90%进行测试，如表2所示。

Table 2. 9 Ground-Truth classes in Pavia University

表2. Pavia University图像中的9个真实类

4.2. 实验设置

本文试验环境：软件为Matlab R2017a，操作系统为Windows 8，处理器Intel Core i5-4200u 1.6 GHz。使用待测像元的总体分类精度(Overall Accuracy, OA)与Kappa系数两个指标衡量各算法的性能。为验证本文算法的有效性，选取SVM，SRC，JSRC和WJSRC算法进行对比，其中WJSRC为本文提出的基于邻域相似性的空谱联合稀疏表示的分类方法。

为确定比重参数λ和相似度阈值τ，分别选取比重参数 $\lambda =1.5,1.8,2.1,2.4,2.7,3.0,3.3,3.6$ 和相似度阈值 $\tau =0.75,0.80,0.85,0.90,0.95$ 进行实验。实验结果如图3所示。

由图3(a)可知，Indian Pines地区比重参数λ = 2.1且τ = 0.85时精度最优。随着比重参数的增大，分类精度提高，在比重参数λ = 2.1时最优；当比重参数大于2.1时，分类精度随着比重参数的增大而降低。τ = 0.85时分类精度最优，当阈值低于或超过0.85时，分类精度随着阈值的减小或增大而降低。

(a) (b)

Figure 3. The influence of specific gravity and similarity thresholds on classification accuracy; (a) Indian Pines; (b) Pavia University

图3. 比重参数λ和相似度阈值对分类精度的影响；(a) Indian Pines; (b) Pavia University

由图3(b)可知，Pavia University地区比重参数λ = 2.4且τ = 0.85时精度最优。随着比重参数的增大，分类精度提高，在比重参数λ = 2.4时最优；当比重参数大于2.4时，分类精度随着比重参数的增大而降低。τ = 0.85时分类精度最优，当阈值低于或超过0.85时，分类精度随着阈值的减小或增大而降低。

4.3. 分类结果

Indian Pines测试集共有16种地物，实验从选出的样本数据集中随机抽取每类样本的10%作为训练样本，其余90%作为测试样本。图4为各算法的实验结果，比重参数λ = 2.1，相似度阈值τ = 0.85。

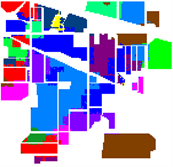(a) (b) (c) (d)

Figure 4. (a)SVM; (b) SRC; (c) JSRC; (d) WJSRC

图4. (a) SVM；(b) SRC；(c) JSRC；(d) WJSRC

表3为Indian Pines图像在10%比例字典情况下，不同算法的总体精度OA和Kappa系数，从表3中可以看出基于邻域相似性的空谱联合稀疏表示算法WJCSR在10%比例字典时总体分类精度比SVM算法、SRC算法和JSRC算法分别高12.64%、13.05%和4.29%。由此可知，高光谱图像的空间信息和光谱信息对高光谱图像分类具有十分重要的意义。

Table 3. OA and Kappa coefficients of Indian Pines under the 10% ratio dictionary

表3. Indian Pines在10%比例字典下的OA和Kappa系数

Pavia University测试集共有9种地物，同样随机抽取每类样本的10%作为训练样本，其余90%作为测试样本。图5为各算法的实验结果，比重参数λ = 2.4，相似度阈值τ = 0.85。

(a) (b) (c) (d)

Figure 5. (a)SVM; (b) SRC; (c) JSRC; (d) WJSRC

图5. (a) SVM；(b) SRC；(c) JSRC；(d) WJSRC

表4为Pavia University在10%比例字典情况下，不同算法的总体精度OA和Kappa系数，从表4中可以看出，基于邻域相似性的空谱联合稀疏表示算法WJCSR在10%比例字典时总体分类精度比SVM算法、SRC算法和JSRC算法分别高18.06%、26.11%和17.19%，依然保持着较好的分类结果。以上实验结果显示，WJSRC在不同的高光谱图像数据下依然保持着较高的分类精度，证明了本文算法具有良好的稳定性。

Table 4. OA and Kappa coefficients of Indian Pines under the 10% ratio dictionary

表4. Pavia University在10%比例字典下的OA和Kappa系数

综合表3与表4的分类结果和图4与图5的分类效果可知：

1) 在两个数据集上对比于其他算法，本文提出的WJSRC算法展现了更好的分类效果，且得到的分类图中本文算法的图像分布较为平滑。由此更加验证了本文算法的有效性和可行性。

2) 在Indian Pines数据集上WJSRC算法比JSRC的分类结果并不是高很多，而在Pavia University数据集上分类结果则有比较明显的提高，主要原因在于Indian Pines数据集上地物更集中，在一定的邻域范围内，距离待测中心像元越近权重越大更有利于提高分类精度，而Pavia University数据集上的地物较之为分散。

3) 对比JSRC算法，本文提出WJSRC算法在空间距离权重的基础上加入了光谱距离权重，对邻域像元特别是边界的不同地物像元的判别有了很大改进，并对每个待测像元求邻域权重通过设定相似度阈值来确定最优邻域大小，因此分类结果较好。

5. 结论

针对传统的稀疏表示分类算法仅利用数据的稀疏相似性，未考虑将数据的邻域信息利用到分类过程中的问题，本文提出了一种新的基于稀疏特性和邻域相似度量的分类方法。该方法通过将兰氏距离作为空间距离权重，并引入光谱距离权重来改善对边界像元分类不完全的不足，二者结合并用于度量待测中心像元与邻域像元的相似性，设定相似度阈值，选取与待测像元相似度高的像元进行联合稀疏表示，最后根据最小残差准则确定待测中心像元的类别，较好地提升了高光谱图像的分类精度。实验结果表明，本文算法能够较好地提高高光谱图像的分类精度，且在不同的试验数据下具备良好的稳定性，进一步验证邻域相似度及空谱结合在联合稀疏表示分类中的必要性。

但是本文算法在求解邻域相似性时存在引入异类地物的风险，对于分布过于密集的区域，存在较多的异类地物，并且其光谱距离相近，此时邻域信息的引入易造成错误分类。基于此，在后续的研究中将考虑寻找更加合适的相似度平衡方法，进一步优化权重，为实现多种特性融合分类打下基础。

参考文献