1. 引言
在如今的现代物流系统中，配送中心的选址是一项非常具有战略意义的活动。科学和合理的将配送中心进行选址可以有效的解决物流成本问题、节约资源、优化物流网络结构及空间布局，可以建立资源节约型物流系统。
同时在现阶段的物流系统中对易腐物品在配送中心的选址，有了更高的要求。且易腐品配送中除了把控固定成本以及运输成本外，还需考虑在此配送中心产品的特殊性，因为易腐品如鲜活农场品随着时间的流逝，其使用价值就会慢慢消失，所以在之后的数学模型中考虑腐蚀速率公式。本文中给定某一个正方形区域来配送易腐蚀物品，在此之中有一些对易腐物品有这需求的客户，要求在此范围内建立一定数量的配送中心，来实现在此区域内对需求用户的物品配送。选址最终的目标就是为了是在此范围内所建立的配送中心各个客户之间形成的配送中心系统的总费用最少。本文根基以上需求建立了关于易腐物品配送中心的选址模型，并结合模植物生长算法求解模型。
2. 文献综述
经过大量的文献资料查找与阅读，对国内外对于配送中心、选址的研究现状大致归纳如下：
蒋长兵等阐述了物流分段选址问题关键算法的运用，于国际物流分段选址之常用分析方法前提下，重点研究了精确重心算法 [1] 。
戴更新等提出混合遗传算法的求解算法，应用在区域配送系统的多配送中心选址题，构建确定性规划模型 [2] 。
姜大立，杨西龙针对易腐物品的特性和连续选址问题的复杂性，建立了一种求解易腐物品配送中心连续选址问题的CAGA算法，此算法为与ALA法结合而成的遗传算法 [3] 。
李彤提出植物模拟生长算法，并将其应用于设备选址问题中。模拟植物生长算法在得到全局最优解的同时，还可以根据设施数量的不同，将全局最优解与局部最优解进行组合，可以建立整体最优的设施布局 [4] 。
李彤和王众托院士提出利用树状网络作为城市底下物流网络结构的方法来解决我国大型城市不断扩张的问题，并利用PGSA得出优化方法 [5] 。
丁雪枫、马良成功将PGSA应用于易腐产品的物流中心选址问题 [6] 。
王莉等学者针对原始PGSA存在生长激素分配不符合植物向光性机理和植物生长方式单一的问题，提出了新的生长素浓度分配方式：利用算法迭代过程中得到的当前最优解(比所有点更接近光源的点)来确定可以生长新枝的节点于对应的生长素浓度，并在植物生长过程中增加了搜索方向，有效提高了算法的全局搜索能力 [7] 。
李苏文分析生鲜食品的特性，得出使固定成本、运输成本和货物损失成本总和最小化为配送中心选址的目标 [8] 。
李寻梦借鉴多种配送中心选址模型与方法，对传统的生鲜食品配送中心选址模型进行改进，建立新鲜度条件下的生鲜食品配送中心选址模型并进行求解 [9] 。
于文娟分析了生鲜配送中心选址的一般方法，从而得出选址问题的解决需要多种方法进行合理有效的组合，得到全局最优解，找出最优选址方案 [10] 。
王淳和程浩忠根据植物的向光性动力机制构造的模拟植物生长算法应用于输电网规划。计算结果表明模拟植物生长算法具有计算模型简单、约束条件处理方便、兼具方向性和随机性的搜索机制等特点，避免了已有的仿生类算法由于一些参数难以确定而陷入局部最优的问题，非常适合于求解输电网规划问题 [11] 。
Guney，Durmus和Basbug将PGSA分别于MTACO，BA，BFA三种智能算法进行比较，比较结果表明PGSA寻求最优解解能力更强，且算法收敛性与计算速度更有优势 [12] 。
经过对文献的参考发现如“重心法”，运用此算法在物流系统选址中是一种静态的选址方法，只将运输成本作为选址决策的唯一决策因素；再如“混合遗传算法”该算法在易腐品选址问题上的应用可能会出现早熟情况，其次对于全局最优解还存在局限性，由于算法本身的局限在得到全局最优的情况下未能达到局部解的最优，解的精算精度还有提升空间。
模拟植物生长算法(plant growth simulation algorithm, PGSA)是由李彤教授于2005年提出的一种模拟植物向光性生长机理的智能算法，由于其参数取值范围宽松、运算时间短，解的稳定性较高，得到了广泛应用。PGSA将待优化问题的可行域当作植物的生长空间，将最优解当作光源，以此模拟真实植物的向光性生长机理(形态素浓度理论)，得到人工植物在不同的光线强度下的快速生长演绎模式 [3] 。与遗传算法为代表的现代启发式算法相比，模拟植物生长算法具有以下优点：① 模拟植物生长算法将目标函数和约束条件分开处理，且无需编码和解码，避免构造新的计算用目标函数，也不存在惩罚函数、交叉率、变异率选取等问题，解的稳定性好；② 模拟植物生长算法具有一个由形态素浓度决定的方向性和随机性平衡比较理想的搜索机制 [11] 。
3. 模拟植物生长
3.1. 模拟植物的生长演绎方式
自然界中某一株植物的生长发育过程即是模拟植物生长算法的灵感来源。描述植物生长发育形式语言的L-系统是Lindenmayer在1968年基于重写规则和分枝规则建立的。
L-系统遵循局部决定系统的生长法则，每个单元的行为只与它周围的单元行为有关，每个单元的无意识行为造成了整体系统的涌现。对植物生长做形式化的描述，可以根据以下几点进行 [2] ：1) 破土而出的茎杆在一些叫做节的部位长出新枝；2) 大多数新枝上又长出更新的枝，这种分枝行为反复进行；3) 不同的枝彼此有相似性，整个植物有自相似结构。
根据单个单元与周围单元的联系度，L-系统可分为“与上下文无关”和“与上下文有关”两种。由于“与上下文无关”的L-系统的重写规则只对单个字符串有效，系统可以无限制生长；“与上下文相关”的L-系统只有当单个字符遇到特定的邻居字符时，重写规则才起作用。为了便于理解，本节在一个特殊的L-系统-OL-系统中演示生成一束分枝的过程，用“()”表示分枝向左生长，用“[]”表示分枝向右生长，生长规则如下：
1：a→c[b]d；2：b→a；3：c→c；4：d→c(e)a；5：e→d
图1为OL-系统中一个分枝的生长过程，这个过程的生长过程规则如表1所示。
Figure 1. Growth of a branch in an OL-system
图1. OL-系统中一个分枝的生长过程
3.2. 模拟植物生长算法
文献 [4] 对模拟植物向光性的概率生长模型进行了研究分析，并提出了求解茎、枝上形态素浓度的计
算方法。设长度为M的树干上有t个生长点，则
对应生长点的形态素浓度为
；同样，设单位长度为m的树枝上有k个生长点
，对应的形态素浓度为
则茎、枝上的生长点形态素浓度值分别如公式(1)、(2)所示：
(1)
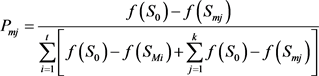(2)
其中，S0为初始可行解，(及种子，初始生长点)；f(*)为生长点的背光函数。式(1)，式(2)抽象概括了生长点形态浓度与光照环境的对应关系，表明各生长点形态素浓度取决于各点相对于树根的相对位置及该位置的环境信息。通过上式，可知所有生长点的形态素浓度值为1，即
(3)
在确定了形态素浓度之后，就可以建立植物的向光性机制，即形态素浓度较高的生长点(细胞)，将具有较大的优先生长机会，其算法可描述为：设在树干和树枝上共有t + k个生长点，
，按照公式(1)与(2)分别计算其形态素浓度值为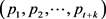
，公式(3)已经证明了，
，因此其空间状态如图2所示。计算机系统不断产生新的随机数，这些随机数就会向[0,1]区间内不断投掷小球，小球落到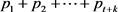
的某一生长状态空间内，所对应的生长点就能得到生长的权力。长出新的长出新的茎、枝，相应的t，k值也进行调整，新生的茎、枝的生长点作为新的生长点加入到下一轮选拔的过程，直至没有新枝出现为止，最终成为一株植物。
Figure 2. State space of Morphin concentration
图2. 形态素浓度状态空间
应用于配送中心选址，PGSA尤其独特的寻优机理，其迭代流程图如图3所示：
Figure 3. Iterative flow chart of PGSA algorithm
图3. PGSA算法迭代流程图
4. 易腐物品配送中心选址模型
本文建立的选址模型是建立与一个二维平面的基础之上，首先是已知在此区间之内我们所需提供易腐品的客户所在地，并且从中选取出一些地址来建立配送中心。从而使在此范围内所建立的配送中心各个客户之间形成的配送中心系统的总费用最少。为满足此目的建立了八个假设：
① 物品产地在配送中心地，各地资源情况一样。
② 每一个客户都有且只有一个配送中心发配物品。
③ 配送中心的仓储能力满足需求。
④ 在配送物品过程中其腐败速率与瞬时物品量成正比。
⑤ 当物品损坏后无法补充。
⑥ 每一客户的需求都为已知。
⑦ 每一对点间的速度都是一致的，客户需求物品都一次运输完成。
⑧ 仓储中的物品损失和仓储费用不计入系统的总费用之中，且在各个地方仓库建设的费用都一致。
根据文献 [3] ，运输费用将由最原始装箱时无损物品数量Wij(0)计算收费，在运输途中会按照一定的速率腐败，则有腐败微分方程公式(4)所示：
(4)
Wij含义为配送中心j到需求点i路途中的无损易腐品量，α系数为腐败速率。
设Tij为配送中心j到客户所在位置i的花费时间；T为配送中心到客户所在位置的运输速度的倒数。Sij为j到i的距离，di为i的易腐物品需求量，如公式(5)所示：
(5)
由以上两个公式(4)公式(5)可以得到
。
定义v为运输率，可得到运输费用如公式(6)所示：
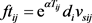(6)
从式(4)、式(5)推倒出配送中心j送至客户i之后腐败损耗，如公式(7)所示：
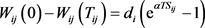(7)
定义z为易腐物品的单位价值，则损失费用如公式(8)所示：
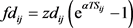(8)
结合式(6)、式(8)并考虑建立配送中心费用，最终得到易腐物品配送中心数学选址模型：
(9)
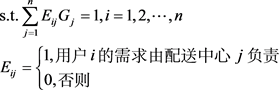(10)
式中，n是客户所需点数，Hj是在j店建立配送中心的费用。
5. 算例及分析
根据现实研究模拟现有一矩形区域此坐标为(0,0)至(100,100)，在此区域内现有40个易腐商品需求的连锁超市，详细坐标见表2。且要在此区域内得到六处配送中心地址，其具体参数详情见表3。通过模拟植物生长算法最后得到6个易腐物品配送中心地址最优解，分别为：
① (17.0022,79.9978) ② (44.9907,59.9956) ③ (57.7756,37.0622) ④ (77.7689,90.8978) ⑤ (22.6933,37.1533) ⑥ (40.9956,5.0111)
其6处配送中心所分别负责需求点见表4。
Table 2. Location of specific coordinates of 40 chains
表2. 40家连锁具体坐标位置情况
Table 4. 6 Chain supermarkets and their demand in six distribution centres
表4. 所选6处配送中心负责的连锁超市及其需求量
将本文算法所得结果与文献 [3] 中遗传算法所得解进行对比如表5，其中可以看出遗传算法所得结果配送中心1与6与PGSA所得结果一样，但其余四处解的地址精度上都有不同程度提升，降低其配送费用，能在达到全局最优解的同时达到局部最优解。
Table 5. Comparison of the optimum location solutions of PGSA and GA distribution centers
表5. PGSA与GA配送中心选址最优解对比
6. 结束语
结合PGSA应用于易腐品配送中心选址实际问题中，利用植物生长的向光性，确定其生长点的概率机制来寻找最优解。在该算例中极好的表达出了其全局搜索能力，也因此算法对其初始生长点的要求略微更宽泛，也没有其他算法对有些参数无法确定的困难，因此它的解相对稳定性较高。本文通过对实际易腐品配送中心选址进行具体应用且与遗传算法所得最优进行对比，展现出了植物模拟生长算法应用性较高且解的精度性更高，对于算法无需连续可微，且并无太多参数要求，对于配送中心选址极为适用。
参考文献