物流金融风险评估模型研究

Logistics Financial Risk Assessment Model Research

摘要: 在物流金融中核心企业的发展对供应链的稳定有着强有力的保障，而物流企业融资难的问题一直没有得到很好的解决，其中难点痛点在于银行不能全面的衡量物流企业业务能力而小样本问题也是银行不能准确分析的一大关键因素。本文从供应链金融中银行的角度针对焦点企业即物流企业贷款的风险评估模型研究，以银行信用和物流企业发展为导向，从经济学的角度构建了一个多指标评估模型，此模型在斟酌企业规模及运营状况的布景下，采用主成分分析法确定供应链及上下游企业的稳定性等因素得出对物流企业的评价指标，设计以支持向量机为模型的物流金融风险评估方法。最后通过具体算例进行仿真测试，结果表明银行在小样本限制条件下能够较好的较为全面的评估物流企业风险给予融资。

Abstract: In this paper, the development of the core enterprise in the logistics financial system has strong guarantee for the stability of the supply chain, and the problem of financing of logistics enterprises has not been well solved, in which the difficult point of pain is not a large measure of the business ability of the bank, but the small sample problem is also a key factor in the failure of bank to ana-lyze accurate analysis. This paper studies the risk assessment model of the core enterprise, namely the logistics enterprise loan, from the perspective of the bank in the supply chain finance. Oriented by the bank risk and the development of the logistics enterprise, this paper constructs a multi-index assessment model from the perspective of economics. Under the background of con-sidering the enterprise size and operation status, this model uses the principal component analysis to determine the stability of the supply chain and upstream and downstream enterprises and other factors to confirm the evaluation index of the logistics enterprise. Finally through the concrete example simulation test, the results show that the bank under the restricted condition of the small sample can better comprehensive evaluation of logistics enterprises to financing risk.

1. 引言

物流金融是在物流营运过程中，与其相关企业通过金融市场和金融机构，为使物流产生的价值的得以增值运用金融工具进行融资和结算的服务活动。由于物流金融使得多方获利，因此供应链中的这种多赢模式在过去几年迅速发展。物流金融的产生与发展扩展了商业银行贷款范围，增加了中间业务收入，极大的加强了银行的竞争力。但由于物流金融本身的特点，它表现出与其他信贷业务不同的信用风险，银行怎样加强对信用风险评估及控制就显得尤为重要。加强对物流金融信用风险的控制以提高供应链物流的运作效率并降低其贷款的风险，可以有效地解决物流企业融资难的问题，具有巨大的发展空间。我国一些物流企业如顺丰、科捷等公司已与银行紧密合作展开信用风险评估及贷款业务，但并未充分利用担保资源。

本文基于上述内容对物流金融风险进行了深入的研究，设计了物流金融风险评价指标体系，构建了物流金融信用风险模型，以期为物流金融业务信用风险管理提供依据。引用的文献中存在以下问题：文献 [1] 评估模型利用灰色三角白化权函数构建，此方法中当离散化数据不稳定时，聚类能力较差且该预测方法只适合短期预测，不适用于长期预测。文献 [2] 是基于模糊综合评判法确定物流金融信用评价模型，因为权矢量条件的约束，相对隶属度权的系数偏小，会出现与矩阵不匹配的情况，导致分辨率低，无法确定分类。

目前多数学者的研究方向主要集中在从供应链上游供应商中小企业为获取贷款的角度分析金融信用风险，或从供应链中采办商生产企业角度分析金融信用风险，而本文是从第三方物流企业的角度进行金融信用风险分析，在供应链上下游企业水平的方向上，更好的评估第三方物流企业使其在供应链大环境下获得更好的发展。

2. 物流金融信用风险指标体系构建

物流金融信用风险评价指标体系的构建，要充分体现供应链背景下物流核心企业融资的特点。本文基于历史经验法和专家调查法的结合，构建评价指标体系，对物流金融信用风险进行了综合分析和评价。本文中构建风险指标体系中的指标以汪涛教授在文献 [3] 经济新常态下中小企业互联网融资风险预警机制体系研究为导向并增加部分指标如供应链中的协调合作能力及信用记录等。

首先，通过分析银行及历史研究者研究的信用评价指标得出的体系，了解到当前指标体系主要体现在行业状况和企业综合实力上。本文考虑了第三方物流核心企业的综合实力和供应链中小企业的经营状况，由此得出的初步指标，见表1：

Table 1. Logistics financial risk assessment index system

表1. 物流金融风险评估指标体系

其中包含定量指标及定性指标，样本数据中包含大量财务数据可用于计算定量指标，计算方法如表2所示。

Table 2. Three-level indicators and index description

表2. 三级指标及指标描述

相关性分析用于计算两两指标间的相关密切程度，相关性指数与密切程度呈正相关关系，一般认为相关系数的临界值为0.6，当指标间相关系数大于该临界值时，需删除其中一个。本文运用软件SPSS15.0计算了本文中指标间相关系数，得出异常指标如表3所示：

Table 3. Indicators with large correlation coefficient

表3. 相关系数较大指标

同时，对定性指标进行量化处理方便后期数据分析，所以在本文中借鉴对相关领域的学者在定性指标量化过程中均采用的专家评分法。根据一定标准，请若干代表性专家凭借经验给出各项目的评价分值，以该分值的平均分为计算得分，达到定性指标定量化。

3. 基于支持向量机物流金融信用风险评估模型

物流金融信用风险评估从行业状况，3PL融资企业营运状况及供应链上下游中小企业资信状况和稳定性考虑是否予以贷款。这是典型的二分类问题，即银行信用风险评估是要对申请贷款企业确定“予以贷款”或“不予贷款”两个其中的一个。支持向量机是机器学习的一种方法，广泛而良好的应用在二分类问题中。支持向量机是Corinna Cortes和Vatnik等在1995年提出的机器学习模型，以VC维理论和结构风险最小的原则，从模型精度和学习能力两角度出发，以获得最好的泛化能力。它更好的适用于求解小样本模型及非线性和高维模式识别方面。

3.1. 数学建模

超平面方程 ${\omega }^{\text{Τ}}x+\gamma =0$ ，其中 $\omega ={\left[{\omega }_1,{\omega }_2,\cdots ,{\omega }_n\right]}^{{\rm T}}$ ， $x={\left[x_1,x_2,\cdots ,x_n\right]}^{\text{Τ}}$

分类间隔方程 $d=\frac{\left|{\omega }^{\text{T}}x+\gamma \right|}{\Vert \omega \Vert }$ ，其中 $\Vert \omega \Vert$ 表示 $\omega$ 的二范数

约束条件 $\{\begin{array}{l}{\omega }^{\text{Τ}}{x}_i+\gamma \ge 1\forall y_i=1\\ {\omega }^{\text{Τ}}{x}_i+\gamma \le -1\forall y_i=-1\end{array}$ ，其中 $y_i$ 为分类标签

优化目标函数即d最大化支持向量上的点 ${\omega }^{\text{Τ}}{x}_i+\gamma =1$ ，任意支持向量上的点 $x_i$

那么，目标函数进一步化简为 $d=\frac{1}{\Vert \omega \Vert }$

1) 线性分类：

进而， $\min \frac{1}{2}{\Vert \omega \Vert }^2\text{s}\text{.t}\text{.}{y}_i\left({\omega }^{{\rm T}}{x}_i+b\right)\ge 1,i=1,2,\cdots ,n$

将二次规划问题转化为对偶问题，即：

$\max Q\left(\alpha \right)={\displaystyle {\sum }_{i=1}^n{\alpha }_i}-\frac{1}{2}{\displaystyle {\sum }_{i=1}^n{\displaystyle {\sum }_{j=1}^n{\alpha }_i{a}_j{y}_i{y}_j{x}_i^{\text{T}}{x}_j}}$

s.t. ${\displaystyle {\sum }_{i=1}^n{a}_i{y}_i}=0$ ，且 $a_i\ge 0,i=1,2,\cdots ,n$

其中 $a_i\ge 0$ 是为求解而引入的拉格朗日系数，求得最优解分类函数为：

$\max Q\left(\alpha \right)=\frac{1}{2}{\displaystyle {\sum }_{i=1}^n{\displaystyle {\sum }_{j=1}^n{\alpha }_i{a}_j{y}_i{y}_j{x}_i^{\text{T}}{x}_j}}-{\displaystyle {\sum }_{i=1}^n{\alpha }_i}$

s.t. ${\displaystyle {\sum }_{i=1}^n{a}_i{y}_i}=0$ ，且 $a_i\ge 0,i=1,2,\cdots ,n$

数据的非100%线性可分的特征，需引入松弛变量，同意部分数据可以处于超平面的错误的一侧。这样能保证优化目标仍保持不变，此时的约束条件为：

s.t. ${\displaystyle {\sum }_{i=1}^n{a}_i{y}_i}=0$ ，且 $0\le a_i\le C,i=1,2,\cdots ,n$

则此时求解的问题变为：

$\min \omega ,b,\xi \varphi \left(\omega ,x\right)=\frac{1}{2}{\omega }^{\text{T}}\omega +C{\displaystyle {\sum }_{i=1}^n{\xi }_i}$ s.t. $$

2) 非线性分类：

$\max Q\left(\alpha \right)={\displaystyle {\sum }_{i=1}^n{\alpha }_i}-\frac{1}{2}{\displaystyle {\sum }_{i=1}^n{\displaystyle {\sum }_{j=1}^n{\alpha }_i{a}_j{y}_i{y}_{j}K\left(x_i,x_j\right)}}$

s.t. ${\displaystyle {\sum }_{i=1}^n{a}_i{y}_i}=0$ ，且 $0\le a_i\le C,i=1,2,\cdots ,n$

求解得到分类函数为：

$f\left(x\right)=\mathrm{sgn}\left({\displaystyle {\sum }_{i=1}^n{a}_i^{*}{y}_{i}K\left(x_i,x_j\right)}+b^{*}\right)$

关于非线性和函数中常用的核函数有：

多项式核函数：维度是 $\left(\frac{m+d}{d}\right)$ 其中m是原始空间维度

高斯径向基核函数： $K\left(x_1,x_2\right)=\exp \left(-\frac{{\Vert x_1-x_2\Vert }^2}{2{\sigma }^2}\right)$

线性核函数： $K\left(x_1,x_2\right)=\langle x_1,x_2\rangle$

为避免高维特征空间而引起的维度灾难，只计算核函数而不需要显示计算非线性函数，以上即为支持向量机，利用得到的分类函数对贷款企业进行分类。

3.2. 模型构建

1) 数据归一化：

数据采集完成后进行数据预处理工作在模型系统中较为关键的一步，原始数据采集时由于并不针对本研究问题，对于直接使用原始数据进行训练效果可能不佳，因此需要通过数据预处理和特征提取达到提升模型精度，而归一化处理让不同维度之间的特征在数值上有一定可比性，提高数据准确性，提升收敛速度。本文实验中采用数据归一化方法为最小-最大标准化法，将特征缩放至特定区间的最小值和最大值之间，或者也可以将每个特征的最大绝对值转换至单位大小。这种方法是对原始数据的线性变换，将数据归一到[0,1]中间。转换函数为：

$x_i=\frac{x_i-{\min }_i}{{\max }_i-{\min }_i}$

2) 核函数的选取和参数的选择：

在选取核函数解决实际问题时，最好的核函数是适用本文数据归纳误差最小的，而高斯径向基(RBF)核函数主要适用于线性不可分但参数少情况。径向基核函数归类于局部核函数，当数据点距离中心点变远时，取值会变小，对噪声有着较好的抗干扰能力。线性核是特殊的RBF核，即带有惩罚参数C的线性核和有参数 $\left(C,\sigma \right)$ 的RBF核具有一样的功能。

其中惩罚参数C用以调节物流金融风险两两指标间的间隔大小与分类准确度偏好的权重，也就是对于误差的容忍度，C越高就越不能容忍出现误差，容易过拟合。核函数g则是决定了样本数据在分类后映射到新的特征空间后的分布， $\sigma$ 很小的话只作用于样本周边，使得未知样本分类结果存在误差，准确率不高。

本文核函数使用PBF核函数，需确定两个参数惩罚参数C和 核函数参数g，g范围在 $\left(0.7,1\right)$ 上具有较好的分类效果，否则容易过早出现过拟合现象，惩罚参数C的范围在 $\left(0,100\right)$ 上。参数值在训练集中确定为 $C=100$ ， $\sigma =10$ 。

4. 实证研究

为确保数据有效性，我们选取300个样本(接近总数2/3)作为训练集，用于构造模型，150个样本作为测试集，用于检验模型的泛化能力。此数据来源于顺丰官网提供的往年数据，得出样本集分布情况如表4所示：

Table 4. Distribution of sample sets

表4. 样本集分布情况

将数据归一化处理后，得到的新数据作为支持向量机的输入数据，用1和0来代表第三方物流企业的信用风险归类类别，即为支持向量机的输出，输出结果如图1所示。

对原始搜集数据进行信度分析，通过SPSS15.0计算得出Cronbrach’s Alpha的值结果如表5所示，根据统计学相关理论可知，当Cronbrach’s Alpha的值大于0.8时，数据可信。因此，本次关于顺丰企业进行的搜查数据具有良好的可信度。

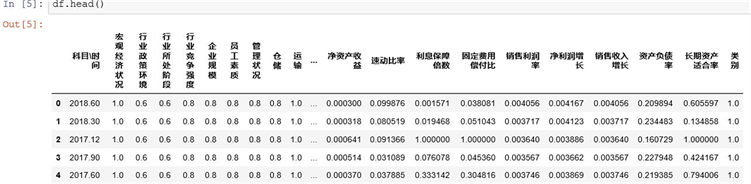
Figure 1. Support vector machine output results

图1. 支持向量机输出结果

Table 5. Reliability statistics

表5. 可靠性统计量

利用支持向量机模型，设置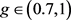， $C=100$ ， $\sigma =10$ 。在物流金融风险评估指标体系下利用支持向量机的方法对训练样本进行训练，记录样本分类结果得出训练集，其次将测试样本集训练，得出分类并记录测试分类结果，对比已有数据，得出分类准确率和正确率结果如图2所示：

Figure 2. Test set accuracy and accuracy

图2. 测试集准确率和正确率

以上结果是因为机器学习算法预测时，因为本身并不知道其中的歧在规则，使用机器学习算法例如线性回归任务在数据集上拟合出来的这个函数，最后得到的函数被称之为模型，数据机就是基于这个模型生成的，所以里面就不包含噪声点，而支持向量机得到的模型精度很高，公式算出来的数据机用一个比较弱的分类器由NFL定理可能会出现比较大的误差，而像SVM这种机器学习是深度学习算法中非常强的分类器，一般不回出现比较多的变差。泛化误差是因为训练样本中存在错误的点，而公式准确直接使训练样本没有错误点，那么模型表现就非常好。

5. 总结

本文在银行角度下对物流金融风险评估进行研究，针对供应链中物流企业的行业状况、自身资信情况及供应链稳定性三个角度运用支持向量机的算法建立一种可广泛应用的物流企业评估模型，采用顺丰速运2008~2018年数据进行实证评估。

银行在针对物流企业风险进行评估时遇到的最棘手的问题一般是业务繁杂数据量少，支持向量机的特性在于小样本中提取分析潜在规则以达成较好的分类器。本文将供应链中对物流企业各环节的影响因素进行更加全面的归类整理，针对数据量少引入机器学习算法，支持向量机其特性是小样本中挖掘潜在规则生成比较强的分类器，具有较好的鲁棒性，银行在针对物流金融企业进行评估时准确分析物流核心业务的权重影响，且该算法具有较好的泛化推广能力，银行在针对中小企业时也可通用此方法进行分析。

针对顺丰公司提供的数据来看，自2017年上市以来公司呈稳定发展趋势，与其上下游企业例如小米科技公司及周黑鸭生鲜公司，并与其供应链公司怡亚通合建供应链数据平台，正确的分析出顺丰公司良好的信用风险，降低银行对其进行贷款时的风险。但对部分中小物流企业在进行风险评估时，由于其数据真实性风险系数较高，且为小样本数据，我们应考虑采用多种模型共同进行分析其风险状况，一来降低其误差增加其变量间因果关系的支持度，二来也可以修正支持向量机的分类结果以保证风险评估的准确度。

行业状况中从宏观环境上分析出当前市场状况良好，国家支持下扩大银行业务量有较好的发展前景，在供应链稳定性中反映出物流核心企业在供应链中核心地位，从这个角度上分析了稳定性影响指标对企业发展的影响，物流企业自身资信情况中分析出关键风险影响指标，从而有助于实现在银行规范对物流企业评估程序和提升标准，可有效地降低业务风险，促进物流金融的进一步发展。