一类改进的随机Runge-Kutta法及应用

An Improved Stochastic Runge-Kutta Method and Its Application

摘要: 本文通过对随机Runge-Kutta法的改进，给出一种四阶随机Runge-Kutta法，并研究了该方法在均值意义下的稳定性。最后，运用此方法对一类随机生物动力系统进行数值模拟，说明了方法的有效性。

Abstract: In this paper, we presented an improved fourth-order random Runge-Kutta scheme for calculating numerical solution to stochastic dynamical system. We also investigated its stability in the sense of variance, and the result obtained is satisfied. By means of the stochastic Runge-Kutta scheme above, we finished numerical simulation for a stochastic biodynamic system. The results certified the effectiveness of the improved scheme.

1. 引言

用常微分方程来描述和解决实际问题，在很多领域有着极其重要的作用。对于常微分方程数值解法的研究已经趋于完善，并取得了大量的研究成果。然而，自然界中充满各种各样的随机因素的干扰，若忽略这些随机因素的影响，就不能精确地描述实际问题。因此，需要引入随机项建立随机动力系统，便可更好地描述实际问题。由于随机微分方程的解析解很难得到，所以探究其数值模拟方法很有意义。Runge-Kutta (龙格–库塔)法是用于求解常微分方程的一种常用方法，它较Euler法有更高的精确度，因此随机微分方程龙格–库塔法的研究非常有意义。Kloeden P.E.构造了随机微分方程的Euler法和Milstein法 [1] ，随机Runge-Kutta法可以通过随机Taylor展开式得到，K. Burrage提出了随机Runge-Kutta法的显式方法 [2] ，胡建成构造了 $It\hat{o}$ 型随机微分方程的一阶、二阶随机Runge-Kutta方法 [3] ，K. Burrage提出了 $Stratonovich$ 型随机Runge-Kutta方法 [4] [5] 。

近年来，一些科研者对三阶、四阶随机Runge-Kutta方法进行了大量的研究 [6] [7] [8] [9] ，其中,钱建成构造了强1阶四级显式Runge-Kutta方法 [6] 。

本文给出了改进的Runge-Kutta方法，并用Mathematica系统编程，实现数值模拟。

2. 两类随机微分方程

考虑如下随机微分方程

$\text{d}X\left(t\right)=f\left(t,X\left(t\right)\right)\text{d}t+g\left(t,X\left(t\right)\right)\text{d}W\left(t\right),X\left(0\right)=X_0$ (1)

其中f为漂移项，g称为扩散项， $W\left(t\right)$ 是布朗运动， $\Delta W\left(t\right)=W\left(t\right)-W\left(s\right)$ 是独立的高斯过程，并且 $\Delta W\left(t\right)~N\left(0,\sqrt{t-s}\right)$ 。

方程(1)的解为

$X\left(t\right)=X\left(0\right)+{\displaystyle {\int }_0^{t}f\left(s,X\left(s\right)\right)\text{d}s}+{\displaystyle {\int }_0^{t}g\left(s,X\left(s\right)\right)\text{d}W\left(s\right)}$ (2)

其中 ${\displaystyle {\int }_0^{t}g\left(s,X\left(s\right)\right)\text{d}W\left(s\right)}$ 是随机积分。

对于Itô型随机微分方程

$\text{d}X\left(t\right)=f\left(t,X\left(t\right)\right)\text{d}t+g\left(t,X\left(t\right)\right)\text{d}W\left(t\right)$ ，有

${\displaystyle {\int }_s^{t}W\left(t\right)\text{d}W\left(t\right)}=\frac{W{\left(t\right)}^2-W{\left(s\right)}^2}{2}-\frac{t-s}{2},\forall t,s\ge 0$ (3)

对于Stratonovich型随机微分方程 $\text{d}X\left(t\right)=f_1\left(t,X\left(t\right)\right)\text{d}t+g\left(t,X\left(t\right)\right)o\text{d}W\left(t\right)$ ，有

${\displaystyle {\int }_s^{t}W\left(t\right)o\text{d}W\left(t\right)}=\frac{W{\left(t\right)}^2-W{\left(s\right)}^2}{2},\forall t,s\ge 0$ (4)

两种微分方程之间的关系是

$f\left(t,X\left(t\right)\right)=f_1\left(t,X\left(t\right)\right)+\frac{1}{2}\frac{\partial g}{\partial X}\left(t,X\left(t\right)\right)g(t,X(t))$

3. 改进的随机Runge-Kutta法

对于一般的常微分方程常用的四阶Runge-Kutta法，即利用如下公式：

$\{\begin{array}{l}{y}_{n+1}=y_n+\frac{h}{6}\left(k_1+2k_2+2k_3+k_4\right)\\ k_1=f\left(x_n,y_n\right)\\ k_2=f\left(x_n+\frac{1}{2}h,y_n+\frac{h}{2}{k}_1\right)\\ k_3=f\left(x_n+\frac{1}{2}h,y_n+\frac{h}{2}{k}_2\right)\\ k_4=f\left(x_n+h,y_n+k_3\right)\end{array}$ (5)

该公式的局部截断误差可达 $\text{O}\left(h^5\right)$ 。由于Runge-Kutta法精确，可减小步长来达到需要的精度，因此

较其他的方法计算误差减小。Butcher [2] 将Runge-Kutta法平行移植到随机微分方程中，得到一类求解随机微分方程数值解的方法——随机Runge-Kutta法

$\{\begin{array}{l}{Y}_i=y_n+h{\displaystyle {\sum }_{j=1}^s{a}_{ij}f\left(Y_j\right)}+Q_1{\displaystyle {\sum }_{j=1}^s{b}_{ij}g\left(Y_j\right)}\\ y_{n+1}=y_n+\frac{h}{2}{\displaystyle {\sum }_{j=1}^s{\alpha }_{j}f\left(Y_j\right)}+Q_1{\displaystyle {\sum }_{j=1}^s{\beta }_{j}g\left(Y_j\right)}\end{array}$ (6)

其中 $i=1,2,\cdots ,s,Q_1~N\left(0,h\right)$ 。

通过不同的参数设定，可以构造不同类型的随机Runge-Kutta法，并且进一步研究其稳定性。大量的学者对随机微分方程的Runge-Kutta法进行了研究，并且利用Butcher提出的彩色树理论，给出了一种四级显式Runge-Kutta方法 [6] 。本文在此基础上做了改进，得到如下计算公式：

$\{\begin{array}{l}{y}_{n+1}=y_n+\frac{1}{12}h\left(7f\left(k_1\right)-f\left(k_2\right)+3f\left(k_3\right)+3f\left(k_4\right)\right)\\ +\frac{1}{72}{Q}_1\left(65g\left(k_1\right)-35g\left(k_2\right)+99g\left(k_3\right)-57g\left(k_4\right)\right)\\ k_1=y_n\\ k_2=y_n+\frac{6}{35}hf\left(k_1\right)+3g\left(k_1\right)Q_1\\ k_3=y_n+\frac{1}{2}h\left(f\left(k_1\right)+f\left(k_2\right)\right)+\left(g\left(k_1\right)+g\left(k_2\right)\right)Q_1\\ k_4=y_n+\frac{1}{3}h\left(f\left(k_1\right)+f\left(k_2\right)+f\left(k_3\right)\right)+\frac{1}{3}\left(g\left(k_1\right)+g\left(k_2\right)+g\left(k_3\right)\right)Q_1\end{array}$ (7)

其中 $Q_1={\displaystyle {\int }_0^{h}o\text{d}B\left(t\right)}$ 。

4. 稳定性分析

对于线性检验随机微分方程

$\text{d}y\left(t\right)=\alpha y\left(t\right)\text{d}t+\beta y\left(t\right)o\text{d}W\left(t\right)$ (8)

初值条件为 $y\left(0\right)=1$ 。方程(8)的解为

$y\left(t\right)=\exp \left\{\left(\alpha -\frac{1}{2}{\beta }^2\right)t+\beta W\left(t\right)\right\}$ (9)

应用Runge-Kutta法，得到迭代式

$y_{n+1}=R\left(h,\alpha ,\beta ,Q_1\right)y_n$ ,

其中 $Q_1=\Delta W_n~N\left(0,h\right)$ ，h为步长， $\alpha ,\beta \in C^1$ 。

定义称 $R_1\left(h,\alpha ,\beta \right)=E\left({\left|R\left(h,\alpha ,\beta ,Q_1\right)\right|}^2\right)$ 是数值方法的均方稳定函数，给定步长h， $h,\left|R_1\left(h,\alpha ,\beta \right)\right|<1$ ，

则称此数值方法是均方稳定的。

定理 对于方程(7)，均方稳定域为

$S=\left\{\left(p,q\right)|\left|R\left(p,q\right)\right|<1\right\}$ ,

其中 $p=\alpha h,q=\beta \sqrt{h}$

$\begin{array}{c}R\left(p,q\right)=1+2p+2q^2+\frac{69p^2}{35}+\frac{127p^3}{105}+\frac{3589p^4}{7350}+\frac{191p^5}{1470}+\frac{19p^6}{900}\\ +\frac{p^7}{588}+\frac{p^8}{19600}+\frac{1121p{q}^2}{168}+\frac{8179p^2{q}^2}{1260}+\frac{7681p^3{q}^2}{2205}\\ +\frac{1060147p^4{q}^2}{907200}+\frac{203183p^5{q}^2}{1058400}+\frac{719p^6{q}^2}{50400}+\frac{77q^4}{6}\\ +\frac{2807p{q}^4}{240}+\frac{23980253p^2{q}^4}{1693440}-\frac{5178589p^3{q}^4}{1411200}-\frac{703111p^4{q}^4}{940800}\\ +\frac{45875q^6}{432}-\frac{509347p{q}^6}{4032}+\frac{3058301p^2{q}^6}{188160}+\frac{12635q^8}{192}\end{array}$ (10)

证明将Runge-Kutta法应用于方程(8)，有

$k_1=y_n$ ,

$k_2=y_n+\frac{6}{35}hf\left(k_1\right)+3g\left(k_1\right)Q_1$ ,

$k_3=y_n+\frac{1}{2}h\left(f\left(k_1\right)+f\left(k_2\right)\right)+\left(g\left(k_1\right)+g\left(k_2\right)\right)Q_1$ ,

$k_4=y_n+\frac{1}{3}h\left(f\left(k_1\right)+f\left(k_2\right)+f\left(k_3\right)\right)+\frac{1}{3}\left(g\left(k_1\right)+g\left(k_2\right)+g\left(k_3\right)\right)Q_1$ ,

设 $p=\alpha h,q=\beta \sqrt{h},Q=Q_1/\sqrt{h}~N\left(0,1\right)$ ，则

$k_2=\left(1+\frac{6}{35}p+3Qq\right)y_n$ ,

$k_3=\left(1+p+\frac{3p^2}{35}+2Jq+\frac{117Jpq}{70}+3Q^2{q}^2\right)y_n$ ,

$\begin{array}{l}{k}_4=\frac{1}{210}(6p^3+41p^2\left(2+3Qq\right)+3p\left(70+144Qq+109Q^2{q}^2\right)\\ +70\left(3+3Qq+5Q^2{q}^2+3Q^3{q}^3\right))y_n\end{array}$ ,

因此， $y_{n+1}=y_n+\frac{p}{12}\left(7k_1-k_2+3k_3+3k_4\right)+\frac{1}{72}qQ\left(65k_1-35k_2+99k_3-57k_4\right)$ ，

其中

$\begin{array}{l}7k_1-k_2+3k_3+3k_4\\ =\frac{1}{70}(6p^3+p^2\left(100+123Qq\right)+p\left(408+783Qq+327Q^2{q}^2\right)\\ +70\left(12+6Qq+14Q^2{q}^2+3Q^3{q}^3\right))y_n\end{array}$ ,

$\begin{array}{l}65k_1-35k_2+99k_3-57k_4\\ =-\frac{1}{70}(114p^3+p^2\left(964+2337Qq\right)+3p\left(-840-1125Qq+2071Q^2{q}^2\right)\\ +70\left(-72-36Qq-202Q^2{q}^2+57Q^3{q}^3\right))y_n\end{array}$ ,

则

$\begin{array}{l}{y}_{n+1}=y_n(1+p+\frac{17p^2}{35}+\frac{5p^3}{42}+\frac{p^4}{140}+Qq+Qpq+\frac{1867Q{p}^{2}q}{2520}+\frac{13}{105}Q{p}^{3}q+\frac{Q^2{q}^2}{2}\\ +\frac{617}{336}{Q}^{2}p{q}^2-\frac{25}{336}{Q}^2{p}^2{q}^2+\frac{101Q^3{q}^3}{36}-\frac{1651Q^{3}p{q}^3}{1680}-\frac{19Q^4{q}^4}{24})\end{array}$

计算二阶矩： $E\left({\left|y_{n+1}\right|}^2\right)=R\left(p,q\right)E\left({\left|y_n\right|}^2\right)$ ；由均方稳定的定义可知，均方稳定域： $R\left(p,q\right)<1$ 。见

图1所示，与文 [5] 中的方法所得稳定区域比较，显然改进后的随机Runge-Kutta法有较大的稳定域，某种程度上显示了本文工作的意义。

注：期望值计算公式： $E\left(Q^{2k+1}\right)=0,E\left(Q^{2k}\right)=\frac{2k!}{k!2^k}$ ；

Figure 1. Compares the stochastic Runge-Kutta method of stability region. The solid line area surrounded by the improved stability region The dotted line area surrounded by stable region before improvement

图1. 随机Runge-Kutta法稳定域比较：实线所围区域为改进后的稳定域，虚线所围区域为改进前的稳定域

5. 随机种群系统的数值模拟

生态系统中的种群并不是单一存在的，由于空间、资源等共同需求的争夺就会有种群之间的相互关系。利用随机微分方程组来描述这一现象更能符合实际情况，但是随机微分方程的解析解不易得到。因此在研究随机的种群模型时 [10] ，通常利用其数值解进行计算机模拟，以此验证理论分析结果。

在此分析三种群随机互惠系统：

$\{\begin{array}{l}\text{d}x=x\left(0.4-0.7x+0.2y+0.4z\right)+{\delta }_{1}x\text{d}{B}_1\left(t\right)\\ \text{d}y=y\left(0.2+0.1x-0.5y+0.3z\right)+{\delta }_{2}y\text{d}{B}_2\left(t\right)\\ \text{d}z=z\left(0.3+0.2x+0.4y-0.8z\right)+{\delta }_{3}z\text{d}{B}_3\left(t\right)\end{array}$ (11)

其中 $B_i\left(t\right),i=1,2,3$ 表示布朗运动， ${\delta }_i,i=1,2,3$ 表示噪声强度，均为正实数。模拟结果如图2、图3所示：

Figure 2. The above is a time course diagram, and the following is a phase diagram. Numerical simulation of parameter ${\delta }_1=0.05,{\delta }_2=0.07,{\delta }_3=0.08$

图2. 上图为时程图,下图为相图在参数 ${\delta }_1=0.05,{\delta }_2=0.07,{\delta }_3=0.08$ 时的数值模拟

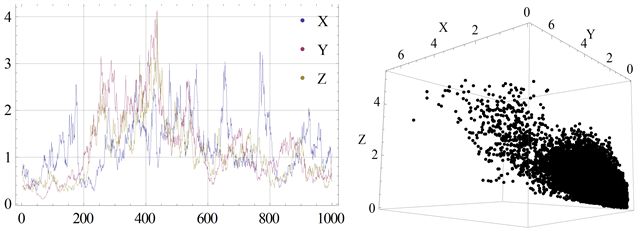
Figure 3. The above is a time course diagram, and the following is a phase diagram. Numerical simulation of parameter ${\delta }_1=0.8,{\delta }_2=0.6,{\delta }_3=0.7$

图3. 上图为时程图，下图为相图，在参数 ${\delta }_1=0.8,{\delta }_2=0.6,{\delta }_3=0.7$ 时的数值模拟

图中可看出种群 $x,y,z$ 为互惠系统，随时间的变化相互促进相互影响。当 ${\delta }_1=0.05,{\delta }_2=0.07,{\delta }_3=0.08$ 时，干扰强度较小时存在平稳分布；当 ${\delta }_1=0.8,{\delta }_2=0.6,{\delta }_3=0.7$ 时，在均值意义下持久生存。

6. 结语

利用数值方法求解微分方程是研究随机动力系统的重要方法。本文给出一种改进的四阶随机Runge-Kutta法，并通过研究其均方意义下的稳定域，说明该方法的优越性。通过实例验证了方法的有效性，并直观地展示了随机因素对种群演化的影响。

致谢

本文工作受到了国家自然科学基金项目(11501410, 51573133, 11672207)，以及天津自然科学基金项目(17JCQNJC03800, 17JCYBJC15700)的资助。

参考文献

NOTES

^*第一作者。

^#通讯作者。