奇异值分解与傅里叶变换相结合的模糊图像分类方法

Blurred Image Classification Method Combining Singular Value Decomposition and Fourier Transform

摘要: 提出了一种基于图像奇异值分解与傅里叶变换相结合的自动区分运动模糊与离焦模糊图像的方法。首先，剔除图像前几个奇异值加权的映射基进行傅里叶变换。其次，以频谱中心为中点取频谱图中合适大小的特征区域，用合适的阈值对该区域二值化。然后，对二值化后的图像进行闭操作与孔洞填充等形态学操作，提取特征连通域。最后，获取特征连通区域的长宽比，在划定阈值后，以长宽比的大小来区分图像的模糊类型。结果表明，该方法具有很好的适用性与模糊识别准确率。

Abstract: A method for automatically distinguishing motion blur and defocused blur images based on com-bining image singular value decomposition and Fourier transform is proposed. First, eliminate the first few mapping bases of image singular value weighting, and do Fourier transform. Secondly, the feature area of the appropriate size in the spectrogram is taken with the center of the spectrum as the midpoint, and the area is binarized with an appropriate threshold. Then, the binarized image is subjected to a morphological operation such as a closing operation and a hole filling to extract a feature connected domain. Finally, the aspect ratio of the feature connected region is obtained, and after the threshold is demarcated, the blur type of the image is distinguished by the aspect ratio. The results show that the method has good applicability and blurred recognition accuracy.

1. 引言

在光学成像系统中，拍摄图片时相机对焦不准确或者目标与相机之间有相对移动都会产生离焦模糊或运动模糊从而导致图像降质，图像降质的后果会对我们获取有用的信息造成干扰。虽然对这类图像进行图像复原可以有效的使模糊图像变清晰，但是在不知道图像降质模型的情况下，很难对模糊图像进行有效的复原。可见，对降质图像的模糊类型进行分类是图像复原前的必要环节。

迄今为止，国内外很多工作者针对以上两种模糊类型进行了大量的研究，并提出了许多模糊图像分类的方法，如利用图像的 $\alpha$ 通道约束 [1] [2] 进行分类，基于神经网络 [3] [4] 的分类，基于梯度或傅里叶谱特征 [5] [6] [7] 的分类，基于模糊核的估计 [8] 和利用图像的局部自相关一致性 [9] 等许多分类方法。本文在不同类型模糊图像的傅里叶变换频谱的特征区域不同的基础上，提出了一种新的基于频谱特征分类模糊图像的方法。

本文我们针对离焦模糊与运动模糊两种模糊类型，将采用图像奇异值分解与傅里叶变换相结合的方法来区分这两类模糊图像。本文结构如下，第二部分介绍数字图像的奇异值分解与模糊图像的频域特征； 第三部分介绍数字图像在傅里叶变换的基础上结合奇异值分解来区分离焦模糊与运动模糊图像的方法； 第四部分介绍结果并对结果进行分析；第五部分对本文进行总结。

2. 数字图像的奇异值分解与模糊图像的频域特征

2.1. 奇异值特征

对于已知图像 $I$ ，它的奇异值分解表达式 [10] 为：

$I=US{V}^T$ (1)

式中 $I$ 为一幅图像， $U$ 和 $V$ 为两个标准正交矩阵， $S$ 为一个对角矩阵，若其对角线上的元素为 ${\lambda }_i$ ，则 ${\lambda }_i$ 为图像 $I$ 按降序排列的非零奇异值。 $U$ 和 $V$ 的列向量分别为 $u_i$ 、 $v_i$ ，k为矩阵的秩。则有：

$\Vert u_i{v}_i^T\Vert =1,i=1,2,3,\cdots ,k$ (2)

$\langle u_i{v}_i^T,u_j{v}_j^T\rangle =0,i\ge 1,i\ge 1,j\le k,i\ne j$ (3)

式(2) (3)表明，可将 $u_i{v}_i^T$ 视为矩阵 $I$ 的一组标准正交基，则式(1)可以转换为：

$I={\displaystyle \underset{i=1}{\overset{k}{\sum }}{\lambda }_i}{u}_i{v}_i^T$ (4)

因此一幅图像可以看作是k个奇异值加权的映射基叠加，如图1所示。权重不同，表明图像所包含对应正交基 $u_i{v}_i^T$ 的信息量不同。往往用前10%甚至前1%个奇异值加权的映射基叠加后的图像就能近似描述原图。图2所示的是Lena图像经奇异值分解的结果。由图2可以看出用图像奇异值分解的方法做主成分分析时，前几个奇异值加权的映射基叠加所形成的图像近似表示的是原图像的主要信息，后面部分奇异值加权的映射基叠加所形成的图像更多表示的是原图像的细节信息。

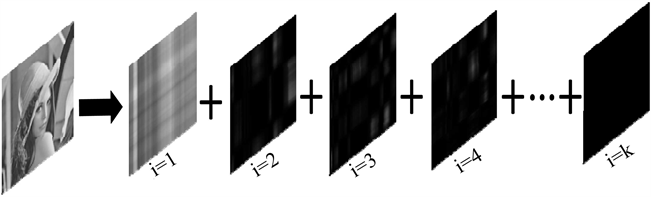
Figure 1. Lena image by singular value decomposition results

图1. Lena图像经奇异值分解的结果

(a) (b) (c)

Figure 2. (a) Standard Lena images; (b) Lena image superimposed on the top 15 singular value weighted maps; (c) Remove the Lena image after the top 15 singular value weighted mapping bases are superimposed

图2. (a) 标准Lena图像；(b) 前15个奇异值加权的映射基叠加后的Lena图像；(c) 去掉前15个奇异值加权的映射基叠加后的Lena图像

2.2. 两种模糊类型的频域特征

对于数字图像这种离散信号，频率大小表示信号变化的剧烈程度，是灰度在平面空间上的梯度。对应到图像中，高频信号往往是图像中的边缘信号和噪声信号，而低频信号包含图像变化频繁的图像轮廓及背景等信号。在将频率零点移到频谱中心后，频谱图的中心对应的是图像的低频信息，而离频率零点越远，点所代表的频率越高。对离焦与运动模糊图像做傅里叶变换，将频率零点移到频谱中心然后取对数，可以发现两种降质图像的对数频谱图所表现的特征不一样 [6] [11] ，如图3是将傅里叶频谱原点移到频谱中心后经离焦与运动模糊降质的Lena图像的对数谱。可以发现，理想情况下离焦模糊图像对数谱中心为同心圆环，运动模糊图像对数谱中心为平行的亮条纹。这是由于离焦模糊图像的低频信息部分的梯度分布是各向同性的，反映在傅里叶频谱图中，频谱中心是圆形；而运动模糊图像低频信息部分的梯度分布是各向异性的，反映在傅里叶频谱图中，频谱中心是线形。因此，可以根据频谱低频信息的形状差异作为我们判断两种模糊类型的判据，能反映这种差异的低频区域则被称之为频谱特征区域。

(a) (b)

Figure 3. Fourier logarithmic spectrum of defocused image and motion blurred image, (a) defocused image; (b) motion blurred image

图3. 离焦模糊图像与运动模糊图像的傅里叶对数谱，(a) 离焦模糊图像；(b) 运动模糊图像

然而，在非理想情况下，通常由于噪声等各种因素的影响，噪点可能会落在模糊图像的边缘细节部分，因此会对傅里叶频谱图中所反映的低频信息区域造成干扰。因而离焦模糊图像的对数谱中心为不一定为同心圆环，还可能是不明显的圆形亮斑，亮斑中可能还有不明显的亮纹干扰，而运动模糊图像的对数谱中心为以频谱中心为交点，相互交叉的亮纹。如图4所示。

(a) (b)

Figure 4. Fourier logarithmic spectrum of blurred image under non-ideal conditions, (a) defocused image; (b) motion blurred image

图4. 非理想情况下傅里叶对数谱，(a) 离焦模糊图像；(b) 运动模糊图像

3. 本文算法

3.1. 傅里叶变换与奇异值分解相结合的特点

虽然傅里叶变换得到的频谱图上的点与原图像上的点之间不存在一一对应的关系，但是去掉原图像前几个奇异值加权的映射基然后进行傅里叶变换可以在一定程度上突出图像的低频信息(如图2)，这样有利于后面对频谱特征区域的分析；且能有效的减弱傅里叶变换谱坐标轴的干扰(如图5)，使后面通过连通区域长宽比来区分模糊图像类型成为可能。

(a) (b)

Figure 5. Fourier logarithmic spectrum of removing the first few singular values weighted, (a) defocused image; (b) motion blurred image

图5. 去掉前几个奇异值加权后的傅里叶对数谱，(a) 离焦模糊图像；(b) 运动模糊图像

3.2. 模糊图像分类的方法

本文中区分离焦模糊与运动模糊的方法大致分为以下3步：

1) 剔除图像前几个奇异值加权的映射基然后进行傅里叶变换。以频谱中心为中点取频谱图中合适大小的中心区域，对该区域进行二值化。

2) 对二值化后的频谱图去除连通域小的区域以消除部分无关信息的干扰，再对二值图进行闭操作与孔洞填充操作，取连通域面积最大的连通域即为频谱特征区域的连通域。

3) 设定合适的阈值，以特征区域二值化图连通域的长宽比作为判据来判断该图像是否为离焦模糊图像或运动模糊图像。

图6是本文算法的流程图，图7是二值化傅里叶谱特征区域的连通域样例图，需要说明的是：

Figure 6. Algorithm flow in this paper

图6. 本文算法流程

① 在本方法中不对傅里叶频谱做对数变换，其原因是对数变换常用来扩展低灰度值，压缩高灰度值，而使低灰度值的图像细节更容易看清，但是这样的话往往会压缩图像灰度值的范围，相对于直接取傅里叶谱而言，取傅里叶对数谱不利于后面对频谱的二值化以突出频谱图像的特征区域。

② 对于取频谱图合适大小的中心区域，该操作的目的是截取频谱图中能反映模糊图像类型的低频信息，去掉大部分的高频信息，所以所截取的区域能正常反映频谱完整的低频信息即可。

③ 本方法是根据频谱低频信息的形状差异作为判断两种模糊类型的判据，该差异反映到具体方法里是二值化后特征区域长宽比大小的不同，我们根据长宽比的大小设定合适的阈值来区分不同特征区域的形状，以达到区分两种模糊类型的目的。经过大量模糊样本实验发现，长宽比的阈值设定在2.5到3.0之间区分的效果较好(图7)。

(a)(b)

Figure 7. The connected domain of the Fourier spectral feature region of the defocused image and the motion blurred image, (a) the defocused image; (b) the motion blurred image

图7. 离焦模糊图像与运动模糊图像的傅里叶谱特征区域的连通域，(a) 离焦模糊图像；(b) 运动模糊图像

4. 实验结果与分析

实验编程环境为Matlab2018b，我们用相机随机拍摄了33张离焦模糊图像与33张运动模糊图像进行实验，如图6是样本图片示例。实验图像分辨率为2992 × 2000，所取的傅里叶谱的中心区域大小为301 × 301，区分模糊类型的最佳阈值设为2.6，当连通域的长宽比大于阈值时判断为运动模糊，反之则判断为离焦模糊。我们分别生成了33张经不同程度的运动模糊和离焦模糊降质的理想Lena图像作为实验结果参考，图像分辨率为500 × 500。表1是分别用图像α通道的方法与本方法区分模糊图像的结果(图8)。

Table 1. Blurred image classification results compared with α channel constraint

表1. 与图像α通道约束对比的模糊图像分类结果

(a) (b)

Figure 8. Image sample taken randomly with the camera, (a) the defocused image; (b) the motion blurred image

图8. 用相机随机拍摄的样本图片示例，(a) 离焦模糊图像；(b) 运动模糊图像

本方法中识别以上两种模糊图像的正确率为90.91%，而Bolan Sun等人所提出α通道约束方法 [1] 的识别以上两种模糊图像正确率为83.33%，与其论文中所说的识别正确率基本一致。实验表明，本方法具有很高的模糊图像分类准确率与算法适用性。

5. 结论

在本文中，我们结合图像的傅里叶变换和奇异值分解提出了一种新的区分离焦模糊与运动模糊图像类型的方法，可以自动区分模糊图像的类型，无需使用神经网络或图像模糊核估计等繁琐的方法。实验表明，本文中所提出的方法适用于不同类型的图像，可用于图像复原、机器视觉等图像处理领域，对以后解决相同类型的问题提供了很高的参考价值。

NOTES

^*通讯作者。