1. 引言
目前块煤分选主要采用的设备是重介质浅槽分选机，其处理量大、分选时间短、分选效果好，逐渐取代了立轮、斜轮等传统的块煤分选设备，得到了广泛应用 [1] [2] [3]。为了进一步提高重介质浅槽分选机的分选效率、精煤产率及适用范围，对不同粒径颗粒在重介质浅槽分选机中运动规律进行探索，帮助我们对重介质浅槽分选机的机体结构进行合理优化，更好地实现煤炭清洁利用这一目标。
在重介质浅槽分选机的研究中，陈志强借助于数值模拟等手段，针对探索重介质浅槽分选机内部的流场形态、重介质及颗粒的运动规律，分析和研究了重介质浅槽分选机内部溢流区、分选区、底流区的流场情况；黄亚飞、陈志强通过PIV技术研究了水平流和上升流比例对流场的影响等；张立文，张毅勤，李国丰，班海俊等人对分选机分选下限做了相关的探索和研究 [4] [5] [6] [7]。
研究表明 [8] [9]，在悬浮液中，煤炭颗粒受入料初始速度和运动方向、悬浮液流变性等因素的影响。在水平流的作用下，处于上层悬浮液中的矿粒朝轻产物的出口方向运动，其水平速度等于或者小于水平流的速度。一般情况下，为了减少煤炭颗粒的错配，使其水平进入浅槽，且速度和水平流的速度保持一致或接近。
在悬浮液中，不仅均质介质水影响煤炭颗粒的运动速度，且原煤颗粒与磁铁矿粉粒径的比值与煤炭颗粒的运动速度也存在一定关系。实验表明，悬浮液的密度和粘度一定时，煤炭颗粒的沉降速度相差不大。在悬浮液中，矿物颗粒的运动分为两种，当颗粒比较粗时与磁铁矿粉粒径相差较大时，为“假定自由运动”，此时可认为悬浮液是均质介质，在这种情况下，颗粒受到颗粒与加重剂颗粒相互作用而产生的阻力的影响不大，仅考虑颗粒受到介质(基本上是悬浮液)的阻力；而当煤炭颗粒的尺寸较小、和磁铁矿粉颗粒的尺寸相近时，悬浮液对于颗粒不再是均匀介质，这时水带来的阻力和与加重质颗粒之间的相互作用的阻力都对颗粒的运动特性产生影响，对单个颗粒的运动而言，后者阻力产生的影响已无法忽略不计。
悬浮液的黏度也影响煤炭在悬浮液中运动，其主要特性参数是流变黏度。选煤用的悬浮液中的固相颗粒经常相互作用 [10]，固相颗粒浓度较低的悬浮液的流变特性接近于牛顿流体，其流变特性由粘度来表示。由于分散相的体积浓度变化会引起粘度的变化，在设定悬浮液的粘度时，需要根据经验公式进行计算。
通过以上对实际生产中煤炭颗粒在重介质浅槽分选机中的运动特性进行分析和研究，下面将模拟不同粒径颗粒在重介质浅槽分选机内部的运动情形。不同粒径的颗粒在重介质浅槽分选机的分选效果会有差别，通过改变重介质浅槽分选机的悬浮液水平流进入速度和悬浮液上升流介质速度，从而得出重介质浅槽分选机内不同粒径颗粒的运动规律及其对分选效果的影响。
2. 数值模型的建立与分析
建立模型过程中的假设：① 以重产物为研究对象进行分析和研究，原煤的入料速度和水平介质速度一致，且立即被水平介质捕获；② 由于重介质浅槽分选机上升流布水板中小孔流动等，使颗粒的运动处于紊流状态，故采用紊流模型；③ 以煤炭颗粒下限6 mm为模拟条件，为了简化模型的计算，将悬浮液视为均质介质；④ 使用重介质悬浮液粘度模型公式计算悬浮液的流变粘度 [11] ：
，
式中：
——煤泥含量；
——剪切速率，s−1；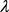
——固体体积浓度；e——自然常数。
2.1. 模型建立与网格划分
建立重介质浅槽分选机模型(图1)，槽体的长和高分别为2540 mm和1450 mm，上升介质槽的高为430 mm，布水板的孔径为13 mm，入口设置为速度边界条件，出口设置为压力边界条件。对其进行网格划分(图2)，网格数量为25,294，网格质量较好，均在0.8以上，可用于计算。
在本次模拟中分别选取悬浮液水平流速度、悬浮液上升流速度对煤炭在分选时有着重要影响的性质作为研究对象。
2.2. 模型可靠性验证
在此次数值模拟中，通过耦合计算方法(Coupled DPM)进行计算，具体过程如下(图3)所示。
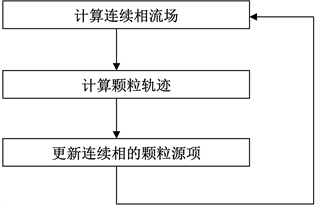
Figure 3. The calculation process of DPM
图3. 耦合计算过程
基于重介质悬浮粘度的经验公式，计算得出了6 mm、13 mm粒径的煤炭在悬浮液粘度不同情况下的自由沉降末速(表1)。使用表1中颗粒直径和悬浮液的粘度数值进行模拟，从而得到对应煤炭颗粒在槽体中的自由沉降末速，同表1中的数值进行比对(图4、图5)。
Table 1. Free settling velocity of different size particles
表1. 不同粒度颗粒自由沉降末速
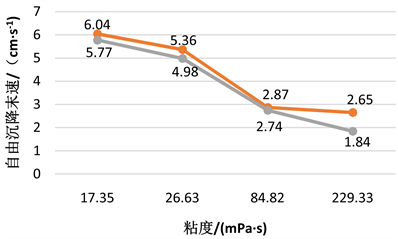
Figure 4. The computation of simulated and calculated value of free settlement velocity of 6 mm particles
图4. 6 mm颗粒自由沉降末速模拟值和计算值对比图
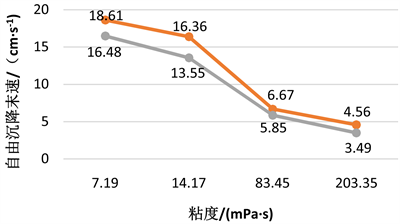
Figure 5. The computation of simulated and calculated value of free settlement velocity of 13 mm particles
图5. 13 mm颗粒自由沉降末速计算值和模拟值对照图
通过对比颗粒自由沉降末速计算值和模拟值可知，对于粒径6 mm的颗粒，颗粒自由沉降速度计算值和模拟值的差值随着粘度的增大先减小后增大，在粘度80~85 mPa∙s时差值最小；对于粒径13 mm的颗粒也存在同样的规律。
颗粒自由沉降速度计算值和模拟值的差值最大为2.15 cm/s，误差在可以接受的范围，对整个实验结果影响较小(在实际分选中)，所以可采用该数值模拟来计算。
3. 模拟结果与分析
该数值模拟中，重产物颗粒的运动轨迹随介质条件的变化而变化。一般情况下认为，在重介质浅槽分选机中，物料停留10 s左右，分选时间太长会降低重介质浅槽分选机处理量，时间太短则物料颗粒还没有实现自由分层即排除分选机，不利于分选。故在此次模拟中根据重产物穿越分选区进入到底流区的时间，不同粒径重产物的运动路径和在Y轴方向的位移，进而推断在该条件下是否达到有效分选。
6 mm至150 mm的颗粒145个，依次排列从入料口上方一次性加入，坐标为(−1260, −1160)，长度为150 mm，原煤同水平介质速度同速加入。
3.1. 水平介质速度对不同粒径颗粒运动的影响
为了探究难选煤颗粒，即分选密度±0.1 g/cm3附近粒度级的分选行为，假定重颗粒的密度为1600 kg/m3，重介质悬浮液的密度为1500 kg/m3，其他相关物理参数如表(表2)。
Table 2. Physical property parameters
表2. 物理性质参数
通过Matlab软件对模拟离散相数据的结果进行处理，得到5组不同粒径颗粒在Y方向的位移和运动时间的关系(图6)。
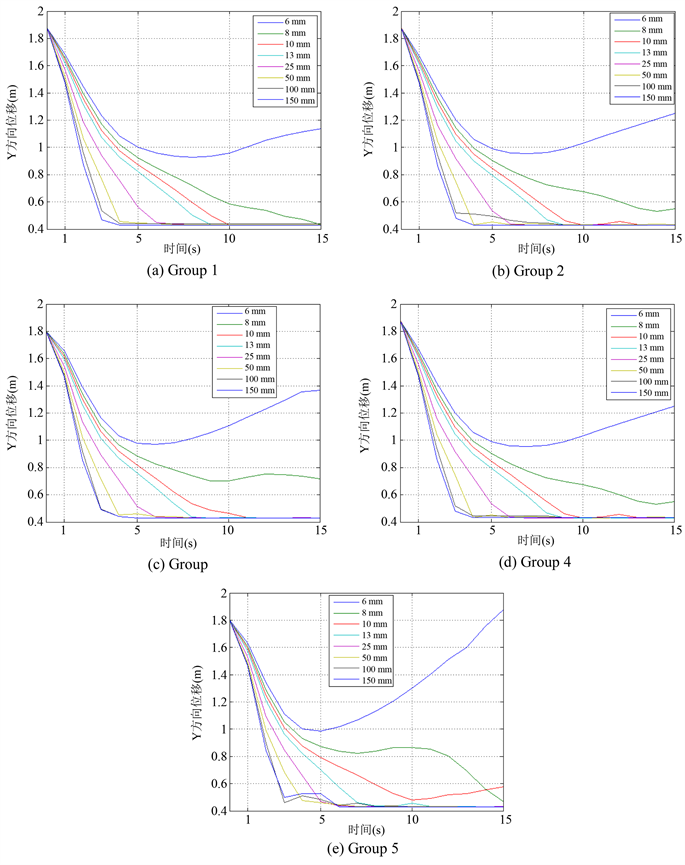
Figure 6. Relation of displacement and time in Y direction
图6. Y方向位移和时间关系图
由图可知，流场相同时，颗粒在Y方向上的位移减小的速度随颗粒直径的减小变慢，到达底部所需要的时间随颗粒直径的减小逐渐增加。当粒度大于13 mm时，颗粒均能在10 s时间内到达分选槽体底部。当粒度小于13 mm时，尤其达到6 mm时，其在槽体内的沉降受到参数变化的影响比较大。实验表明，在分选时间为10 s时，Group 1的条件下可达到最佳分选效果，分选下限为8 mm。
3.2. 上升介质速度对不同粒度颗粒运动的影响
水平介质速度延用group 1的参数、角度，其他参数和3.1相同，对上升介质速度进行研究，具体参数选取如表(表3)。
Table 3. Physical property parameters
表3. 物理性质参数
根据上述参数在Fluent中得到颗粒的运动路径，通过Matlab得到不同上升速度介质速度下，不同粒径颗粒在Y方向的位移和时间的关系(图7)。
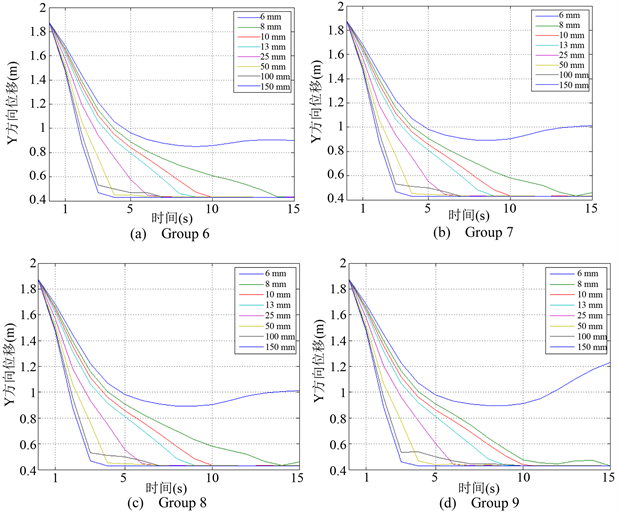
Figure 7. Relation of movement time and displacement in Y direction
图7. 运动时间和Y方向位移关系图
由图可见，上升流速度不同时，不同粒径的颗粒沉降相同距离时所需时间不同，时间随粒度的降低增加。对粒径大的颗粒(10 mm及其以上的颗粒)而言，上升介质速度的增加对其在Y方向上的位移的影响较小，而对粒径较小的颗粒，受到的影响较大。Group 9图中8 mm粒径的颗粒分选更有效，因此分选下限为8 mm时更有利于分选。
4. 结论
通过对不同粒径颗粒在不同重介质悬浮液性质下的运动行为的模拟和颗粒X方向、Y方向位移和时间的关系的对比分析，可以得到如下结论：
1) 悬浮液密度为1500 kg/m3，固体颗粒密度为1600 kg/m3时，13 mm粒径及以上的颗粒受重悬浮液性质改变的影响不大，10 s内固体颗粒均能完成沉降，成为重产物。
2) 上升流速度为0.36 m/s，水平流速度为(0.22, −0.185)时，8 mm粒径及以上的颗粒可以实现有效分选。
3) 上升流速度为0.36 m/s，水平流速度为(0.22, −0.185)时，小于6 mm的颗粒基本不能在有限时间内完成沉降，且离溢流口较近时，易随轻产物夹带排出，造成精煤污染，降低分选精度。
4) 当分选下限降为8 mm时，可以满足重介质浅槽分选机的分选精度。