汽车天窗耦合风振噪声规律及机理研究

Research on Regularity and Mechanism of Vehicle Coupling Sunroof Buffeting Noise

摘要: 风振噪声是汽车行驶过程中车窗开启时普遍存在的问题，本文利用LBM-LES方法对天窗风振噪声特性进行研究。计算分析了不同来流速度、不同天窗开度以及天窗与侧窗耦合工况下的天窗风振噪声，结果表明：发生Helmholtz共振的来流速度下风振现象最明显；风振噪声随天窗开度大小的增大而增大；风振噪声产生机理：天窗开口处剪切层内涡的周期性脱落导致乘员室腔体内压力呈周期性脉动；左后侧窗–天窗完全开启工况下无“通风效应”；由于流体的直接作用，在垂直于开启的车窗方向上，风振噪声强度从窗口向内依次递增。

Abstract: Wind buffeting noise as popular problem exists in the vehicle driving process when windows opened. In this paper, the characteristics of sunroof buffeting noise are studied by LBM-LES simu-lation. The sunroof buffeting noise under conditions of different speeds, different opening size and different combined opening pattern of sunroof and side-window is simulated and analyzed. The results demonstrate that the most obvious phenomenon of sunroof buffeting occurs at the speed which Helmholtz resonance arises. The buffeting noise increases with the increase of sunroof opening size. The mechanism of sunroof buffeting is that the periodic pressure fluctuation of the cabin is caused by periodic vortex shedding in the shear layer of sunroof opening. The “aeration effect” does not exist when the left-front side window and sunroof are opened. Because of the direct action of fluid, in the direction perpendicular to the open window, the buffeting noise increases from the window to the inside.

1. 引言

风振是汽车天窗或侧窗开口处涡的周期性脱落引起的车内压力周期性脉动现象，这种频率在20 Hz左右，强度高达100 dB以上的风振噪声，使驾驶员感到烦躁和疲倦，严重影响了驾驶员和乘员的舒适性 [1] 。有调查显示在车主对气动噪声问题的抱怨中，风振噪声问题占50% [2] 。因此，在汽车开发前期，对风振噪声的研究意义重大。

汽车风振噪声最早被称之为风律动(Wind Throb)，早在上世纪60年代，W. K. Bodger和C. M. Jones 就以实验的方法对此进行了研究 [3] 。上世纪90年代后，计算机技术迅猛发展，在对汽车风振噪声的研究中，CFD技术的运用也越来越成熟。2004年，AN等人对某SUV的侧窗风振噪声进行了仿真，并分析了网格尺寸与空气可压缩性对仿真结果的影响 [4] 。2006年AN等人又对汽车天窗风振噪声的机理进行了探索，并仔细研究了天窗导流板的参数(导流板高度、安装角度)及天窗玻璃开启程度对风振噪声的影响 [5] 。2010年，康宁等人对有天窗简化的Golf1.6轿车进行仿真，随着天窗后移及加宽，得出了监测点处的声压级逐渐减小的结论，并得到了较合理的天窗尺寸及安装位置 [6] 。2011年，胡亚涛等人研究表明产生风振现象时，除了特征频率下的风振噪声，还存在着较大范围的随着流速的增大而显著增加的宽频气动噪声 [7] 。

目前，国内外学者对风振噪声进行了大量的研究，而对天窗不同开度下以及天窗与侧窗组合开启下的风振噪声特性研究比较匮乏，所采用方法也多为求解大涡模拟过滤后的N-S方程。本文应用格子玻尔兹曼法(LBM)结合大涡模拟(LES)对某实车模型在不同工况下的天窗风振噪声进行数值模拟分析，探究其产生机理与相应规律，为后期针对性的降噪设计提供理论依据。

2. 数值计算方法

2.1. 格子玻尔兹曼方法

格子玻尔兹曼法是从介观层面上描述流体状态，相比于传统CFD方法具有低数值耗散的优势，能捕捉流体压缩性影响从而精确模拟与噪声关联的压力脉动以及其传播过程。Boltzmann方程可用以下微分方程 [8] 描述：

$\frac{\partial f_i}{\partial t}+c_i\cdot \nabla f_i+\frac{F}{m}\cdot \frac{\partial f_i}{\partial c_i}={\Omega }_i\left(f\right)$ (1)

式中，F为作用于系统外力。f为关于位置r、速度c和时间t的粒子分布函数。Ω为碰撞算子，因Ω是关于f的函数，Boltzmann方程求解困难。因此引入BGK [8] 近似碰撞算子模型，其具体形式如下：

${\Omega }_i\left(f\right)=\omega \left(f_i{}^{eq}-f_i\right)=\frac{1}{\tau }\left(f_i{}^{eq}-f_i\right)$ (2)

式中， $\omega =1/\tau$ 。为碰撞频率， $\tau$ 为松弛因子。 $f^{eq}$ 为局部平衡分布函数。当确定合适的粒子平衡分布函数 $f^{eq}$ 时，基于Chapman-Enskog展开和Taylor级数展开，(1)式可回归到N-S方程组。

2.2. 大涡模拟

LBM方法数值耗散低，LES采用亚格子模型。本文使用的WALE模型，涡粘度定义如下：

$v_t=\rho L_s^2\frac{{\left(S_{ij}^d{S}_{ij}^d\right)}^{\frac{3}{2}}}{{\left({\bar{S}}_{ij}{\bar{S}}_{ij}\right)}^{\frac{5}{2}}+{\left(S_{ij}^d{S}_{ij}^d\right)}^{\frac{5}{4}}}$ (3)

$S_{ij}^d=\frac{1}{2}\left({\bar{g}}_{ij}^2+{\bar{g}}_{ji}^2\right)-\frac{1}{3}{\delta }_{ij}{\bar{g}}_{kk}^2$ (4)

${\bar{g}}_{ij}=\frac{\partial v_i}{\partial x_j}$ (5)

式中： $L_s=\min \left(kd,C_{\omega }{\Delta }^{\frac{1}{3}}\right)$ ，其中k为冯卡门常数，d为到壁面最近的距离， $C_{\omega }$ 为LES模型常量。

3. 数值计算方案

3.1. 计算域及格子尺度

本文所采用的实车模型如图1所示，为提高计算效率，在不影响计算精度的前提下，对车身进行了简化处理，略去了雨刮器等小附件；由于研究的是天窗开启工况，保留大部分内饰。实车模型长为4812 mm，宽2153 mm，高1348 mm。

Figure 1. Vehicle model

图1. 实车模型

本文所采用的计算域为包围汽车模型的长方体如图2所示，长约10倍车长，宽约5倍车宽，高约4倍车高。其中，车头距入口3倍车长，车尾距出口6倍车长。

Figure 2. Computational domain model

图2. 计算域模型

粒子与传统网格相似，其密度同样影响计算精度，粒子越密，计算精度越高。但粒子数目的增加，相对耗费的计算资源也越多。综合考虑计算精度和计算资源的因素，将流体域内粒子密度分为两层，车身附近区域进行加密，为捕捉车窗开口处流体发展变化情况，对车窗开口的附近区域再局部加密。最终初始粒子数为1300万左右，如图3所示。

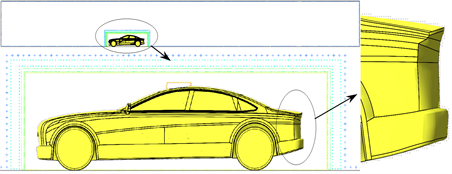
Figure 3. Initial particle distribution in computational domain

图3. 计算域的初始粒子分布图

本文通过实车模型气动阻力系数的仿真计算验证粒子无关性，结果如图4。

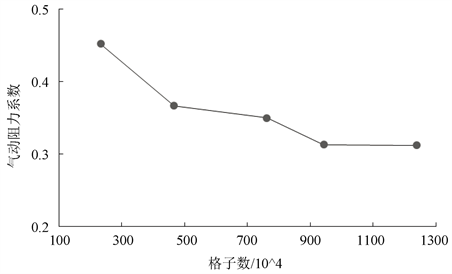
Figure 4. Particle independence verification

图4. 粒子无关性验证结果图

由上图可知，粒子数从900万增加到1200万时， $C_d$ 值几乎无变化，可认为粒子到900万之后已达到格子无关性要求，本文选取的粒子数为1300万。

3.2. 计算方法

本文应用基于LBM方法的商业软件Xflow的数值计算，所采用的边界条件如下表1。

Table 1. Boundary conditions

表1. 边界条件

本文采用自适应粒子优化模式，当计算域内流场发展时，Xflow能在上一帧粒子分布的基础上重新调整粒子。监测点位置为正副驾驶员的左、右耳旁，拟分析频率最高为1000 Hz，计算时间为1.5 s，由于流场从开始到充分发展之间有一个过程，计算结果取后0.75 s的数据。

4. 天窗风振噪声分析

4.1. 不同来流速度下天窗风振噪声分析

实车模型的几何尺寸如下：天窗全开尺寸为0.31 m × 0.9 m，天窗开口厚度为0.06 m，乘客室腔体体积为2.44 m³。根据文献中Helmholtz共振的固有频率预估公式 [9] 为：

$f_a=\frac{c}{2\pi }\sqrt{\frac{S}{V\left(h+\frac{\pi D_h}{4}\right)}}$ (6)

式中， $D_h$ 为天窗全开面积的等效水力直径；S为天窗全开面积；c为声速；V为乘客室腔体体积；h为天窗开口厚度。而文献中提出的开口处剪切层内涡脱落频率 $f_b$ 的预估公式 [10] 为：

$f_b=\frac{1}{3}\left(n-\frac{1}{4}\right)\frac{u}{L_N}$ (7)

式中，n为剪切波模态数， $n=1,2,3$ (n > 3未实验论证)；u为来流速度； $L_N$ 为天窗开度。由(6)式估算出乘员室腔体的固有频率 $f_a$ = 28.16 Hz。由于天窗开口处剪切层涡对乘员室腔体内空气有周期性作用，当脱涡频率近似于乘员室腔体固有频率时，发生Helmholtz共振。由 $f_a=f_b$ ，推算出产生Helmholtz共振的大致来流速度范围，当剪切波模态数n = 1时，u = 34.92 m/s；当n = 2时，u = 14.97 m/s，因此得发生共振的来流速度在14.97~34.92 m/s之间。

计算结果取驾驶员右耳处监测点数据为例，天窗全开工况下风振噪声随来流速度的变化关系如图5所示，纵观所有工况，峰值声压对应的频率与来流速度成正相关性，与(7)式呈现规律相同；而峰值声压随来流速度的增加先逐次升高，在来流速度增至25 m/s时，峰值声压达到最大值，为135.67 dB，其对应频率为28.00 Hz。后随着来流速度的继续增加，峰值声压开始下降。Helmholtz共振的发生频率与(6)式估算值相差小于0.2 Hz，证明了计算结果的正确性。

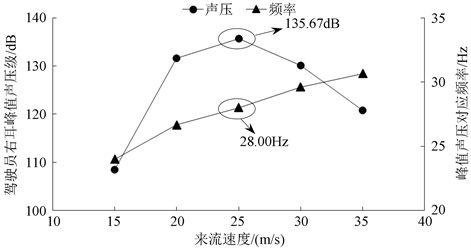
Figure 5. Variation of peak sound pressure and frequency with different velocity

图5. 驾驶员右耳峰值声压频率随来流速度变化

取风振噪声最强的工况：来流速度25 m/s为例，正副驾驶员左右耳处的声压频谱图如图6所示。四个监测点处声压频谱图在低频的时候几乎重合，这是由于风振现象属于低频现象(一般在20 Hz左右)，其波长跨度远超乘员室腔体尺寸，不同位置的风振特征几乎相同。图中峰值对应的频率全为28.00 Hz，声压分别为136.26 dB，135.67 dB，135.69 dB，136.32 dB。

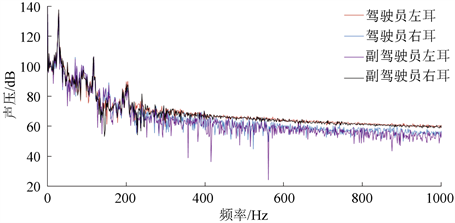
Figure 6. Sound pressure spectrogram of each monitoring point at 25 m/s

图6. 来流速度为25 m/s时各监测点声压频谱图

4.2. 不同开度下天窗风振噪声分析

由(6)式和(7)可知天窗开度对风振噪声有非常重要的影响。本文在来流速度为25 m/s的工况下，以驾驶员右耳监测点为例，天窗风振噪声随开度的变化曲线如图7所示。

由上图可知在天窗开度小于40%时，几乎无明显风振现象，当天窗开度大于60%时，风振现象明显。总体上风振噪声随开度的增加而增加，其峰值对应的频率随开度先增大后减小，波动范围在28 Hz上下。

4.3. 天窗风振噪声机理分析

天窗开口处剪切层作用于乘员室腔体内空气的压力随时域变化而变化，根据文献中的研究表明 [11]

$P=\frac{F}{l}=\rho \Gamma \left(t\right)u_c/l$ (8)

式中，p为开口处涡的运动对乘员室腔体内空气的扰动压力；F为开口处的激励力； $\Gamma \left(t\right)$ 为涡旋环量， $\Gamma \left(t\right)=0.5u_{\infty }^2$， $u_{\infty }$ 为自由来流速度； $u_c$ 为开口处涡的迁移速度；l为开口流向上的尺寸；ρ为空气密度。

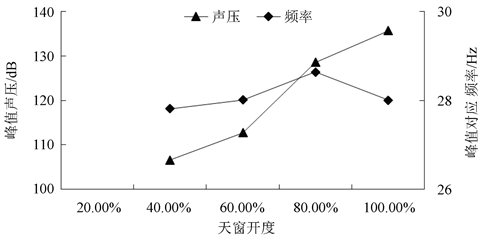
Figure 7. Variation of peak sound pressure and frequency with different openings

图7. 驾驶员右耳处声压峰值与频率随天窗不同开度变化曲线

由(8)式可以得知乘员室空腔内的压力脉动与开口处涡的发展变化有关。取上述来流速度25 m/s工况，由共振频率 $f_a$ = 28.00 Hz得涡的脱涡周期T = 0.0357 s，取一个周期0.9645~1.0002 s内，9个不同时间点驾驶员右耳的脉动压力(图8)与对应时间点流体静压的变化(图9)来解释天窗风振噪声的产生机理。

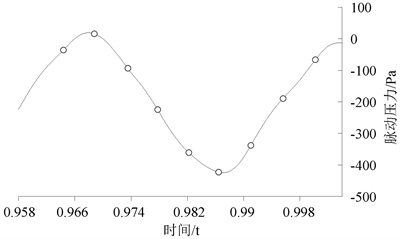
Figure 8. Fluctuation pressure in driver’s right ear in a period

图8. 一个周期内驾驶员右耳处脉动压力

(a) t = 0.9645 s (b) t = 0.9689 s (c) t = 0.9737 s (d) t = 0.9778 s (e) t = 0.9825 s (f) t = 0.9869 s (g) t = 0.9914 s (h) t = 0.9958 s (i) t = 1.0002 s

Figure 9. Static pressure distribution clouds of passenger chamber

图9. 乘员室腔体内压力云图

在t = 0T时，靠近天窗前缘位置逐渐形成一个中心为低负压的涡核，乘员室腔体内驾驶员右耳处监测点压力为正且较大。在t = 1/8T时，涡核在往天窗后缘运动过程中逐渐变大，监测点处压力上升至最大正压。在t = 1/4T、3/8T时，涡核继续向后缘迁移，涡的体积持续增大，且涡核处负压与驾驶员右耳压力持续降低。在t = 1/2T时，涡开始触碰天窗后缘，出现细微破碎的同时产生的压力波向四周辐射，监测点处压力继续下降。在t = 5/8T时，涡核完全碎裂，破碎后的小涡向乘员室腔体运动，并逐渐耗散，低负压范围充满整个乘员室腔体，监测点处压力降到最低。在t = 3/4T时，第一个涡的耗散接近尾声，监测点处压力回升。在t = 7/8T时，第一个涡完全耗散，同时监测点处压力持续上升。在t = 1T时，第二个涡经过发展后与t = 0T时呈现的状态几乎相同，表示一个脱涡周期的结束。

4.4. 天窗、侧窗耦合风振噪声分析

略去对称工况，来流速度为25 m/s，取以下两种组合：左前侧窗–天窗，左后侧窗–天窗。每种组合中每扇窗又以50%开度为间隔排列组合成4种工况，四个测点在每种工况下的声压峰值与对应频率如图10、图11所示。

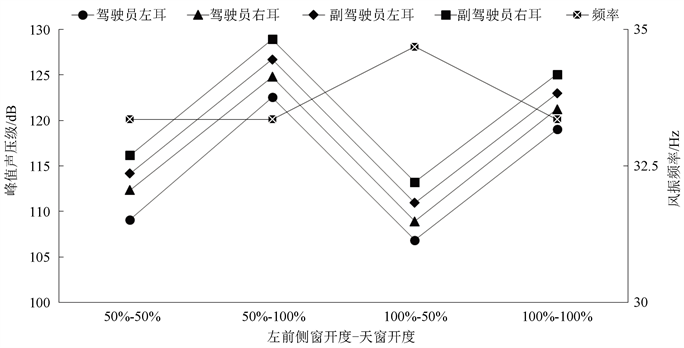
Figure 10. Variation of peak sound pressure and frequency with different combined opening pattern of left-front side window and sunroof

图10. 左前侧窗–天窗不同开度下声压峰值与频率变化曲线

从图10可以看出，四测点的声压峰值在天窗全开的工况较高，最大值出现在左前侧窗50%开度和天窗全开时，其峰值分别为122.53 dB，124.80 dB，126.72 dB，128.94 dB，对应频率为33.35 Hz。四测点的声压峰值：驾驶员左耳 < 驾驶员右耳 < 副驾驶员左耳 < 副驾驶员右耳。左前侧窗–天窗全开对比天窗单全开声压下降相对明显(“通风效应”)。

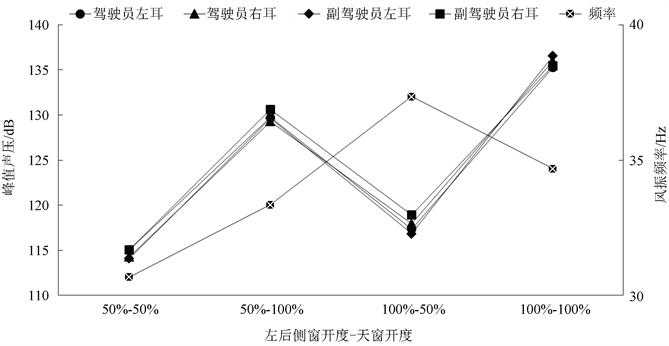
Figure 11. Variation of peak sound pressure and frequency with different combined opening pattern of left-rear side window and sunroof

图11. 左后侧窗–天窗不同开度下声压峰值与频率变化曲线

从图11可以看出，四测点的声压峰值曲线几乎重合，且同样在天窗全开的工况较高，左后侧窗50%和天窗100%时，其峰值为129.74 dB，129.29 dB，129.66 dB，130.62 dB，对应风振频率为33.35 Hz。左后侧窗(50%)–天窗(全开)耦合工况对比天窗单全开工况峰值声压下降5 dB以上，存在“通风效应”；最大值出现在左后侧窗和天窗开度都为100%时，其峰值分别为135.46 dB，136.55 dB，135.99 dB，135.28 dB，对应频率为34.68 Hz。左后侧窗–天窗全开对比天窗单全开工况峰值声压几乎相等，无“通风效应”。

纵观上述工况，两车窗组合开启的峰值声压对应频率都在30~40 Hz之间。风振噪声的最大值出现在两侧窗开度都在“最佳风振开度”(单开时风振噪声最大开度)下。当监测点被流体直接作用时，产生的随机性压力脉动干扰了车窗开口处剪切层对乘员室腔体内空气的周期性作用，风振现象较弱，且四个监测点的声压峰值从窗口向内依次递增，即离窗口越远声压级越高，而流体不直接作用监测点时，四监测点声压峰值几乎相等。在“平衡”开启的工况下无“通风效应”，即左后侧窗–天窗完全开启时，声压峰值与天窗单开时无明显变化。这是因为风振现象大致可解释为开窗口剪切层流体通过对乘员室腔体内部气体周期性作用，产生压力的周期性脉动。当车窗“非平衡”开启时，从作用力较强的车窗侵入的气流可从作用力较弱的车窗部分导出；而车窗“平衡”开启时，两窗口的作用力大致相等，导出效果有限；两窗口剪切层的作用力相差越大，“通风效应”越明显。

5. 结论

1) 汽车天窗风振噪声随来流速度的增加先增强后减弱，对于本款车当来流速度为25 m/s时，剪切层的脱涡频率与乘员室腔体固有频率相接近，发生Helmholtz共振，产生风振噪声最强，峰值声压为135.67 dB，对应频率为28.00 Hz；

2) 天窗风振噪声随天窗开度的增大而增大。对于本款车当来流速度为25 m/s时，当天窗开度小于40%时几乎无明显风振现象，当天窗开度大于60%时，风振现象明显；

3) 天窗风振噪声产生机理：剪切层涡的周期性脱落及其后续的发展过程致使乘员室腔体内压力脉动呈周期性变化；

4) 监测点被流体直接作用时，产生的噪声与风振噪声相叠加，风振现象较弱，垂直于车窗开口向内声压峰值依次递增，流体不直接作用监测点时，声压峰值几乎相等；

5) “通风效应”只出现在车窗“非平衡”开启的工况，车窗“平衡”开启工况与车窗单开时声压峰值变化幅度不大。