基于缩尺斜拉桥模型的结构损伤分析试验研究

Experimental Study on Structural Damage Identification Based on a Scale Cable-Stayed Bridge Model

摘要: 微小的结构损伤可能引起大型工程结构的破坏性失效和灾难性事故，为解决该类损伤识别问题，需要寻找有效的损伤识别参数。基于某缩尺斜拉桥模型的加速度数据，本文研究了模态频率、模态确认准则、以及模态坐标置信因子三种基于结构振动模态的损伤识别方法。首先在MATLAB中建立了结构的有限元模型，进行了损伤识别参数的敏感性分析；然后在缩尺模型上进行了振动试验，比较验证了三种损伤识别方法的效果。研究表明，三种方法能够识别出结构较为明显的损伤，但是对微小的损伤不敏感。

Abstract: Small damage of a component would probably cause the failure of the whole structure and even induces a disaster. In order to identify this type of damage, effective damage indices were required. Based on the acceleration data of a scale cable-stayed bridge model, three damage identification methods based on structural vibration modes, namely modal frequency, modal confirmation cri-terion (MAC) and modal coordinate confidence factor (COMAC), are studied in this paper. Firstly, the finite element model of the structure is established in MATLAB, and the sensitivity analysis of damage identification parameters is carried out. Then vibration tests are carried out on a scale model to verify the effectiveness of the three damage identification methods. The research shows that the employed methods manage to identify the obvious damage of the structure, but they are insensitive to minor damage.

1. 引言

近年来，随着我国桥梁建设事业的发展，众多已建成桥梁的管养维护需求日益扩大，促使桥梁结构健康监测技术成为桥梁学术界与工程界关注的热点 [1] 。桥梁健康监测技术的核心问题之一是损伤识别。针对这一问题，目前得到普遍认同的就是结合系统识别、振动理论、振动测试技术、信号采集与分析等跨学科技术的试验模态分析法。该方法通过分析结构的加速度响应数据，获取出特定的损伤识别参数，进而利用损伤识别参数判断结构是否出现损伤 [2] 。

在此背景下，基于某缩尺斜拉桥模型的加速度数据，本文研究了模态频率、模态确认准则(MAC)以及模态坐标置信因子(COMAC)三种基于结构振动模态的损伤识别方法的效果。研究分为两部分，第一部分为基于有限元模型数值响应的损伤识别参数敏感性分析，第二部分为基于缩尺模型振动试验响应的损伤识别参数有效性分析。

2. 缩尺模型

本文的研究对象为某缩尺斜拉桥模型。模型采用铝合金管材制作，为双塔半漂浮体系斜拉桥，基础锚固于试验室地面。模型的桥塔高1.2 m，跨径分布为0.6 + 0.6 + 3.6 + 0.6 + 0.6 = 6 m。模型两侧边跨各设1个辅助墩和1个边墩。主梁形式为梯状双主梁，拉索形式为弹簧和钢丝。此外，缩尺模型上还配备了完备的健康监测系统，包括应变计、加速度计、位移计以及温湿度计。该缩尺模型的基本信息如图1所示。

模型在设计时便考虑了损伤识别试验的需求，进行了模拟损伤的设计。通过拆装模型构件，可以模拟质量损失、主梁刚度损伤以及拉索刚度损伤。由于实际桥梁很少在产生质量损失的同时而不产生刚度损伤，本试验主要研究主梁刚度损伤与拉索刚度损伤的识别。

3. 损伤识别参数敏感性分析

3.1. 模态分析正问题

本文主要研究基于结构模态的损伤识别参数，因此首先需要进行结构模态分析。桥梁在运营期间主要承受竖向荷载，因此本文主要聚焦于缩尺斜拉桥模型的前3阶竖向模态。为了得到该缩尺斜拉桥模型的模态信息，本研究分别在Midas Civil有限元软件中建立了缩尺模型的空间三维有限元模型，以及在MATLAB数值计算软件中建立了缩尺模型的平面有限元模型，然后对有限元模型进行模态分析，得到缩尺模型的前3阶竖向模态如表1所示。

(a) 缩尺模型尺寸图(b) 缩尺模型实物标识图

Figure 1. Diagram of the scaled model

图1. 缩尺模型示意图

Table 1. Vertical modal information of the scaled model

表1. 缩尺模型的竖向模态信息

之所以在使用商用有限元软件Midas Civil建立空间有限元模型之余，仍然使用数值计算软件MATLAB建立了平面有限元模型，是因为MATLAB编写的有限元程序可修改性更强，便于进行损伤识别参数敏感性分析。对比表1中比Midas Civil和MATLAB有限元模型的动力特性可以发现，二者在振型和频率上都非常接近。这意味着使用MATLAB有限元模型进行结构损伤的参数化分析是可靠的。

3.2. 拉索刚度损伤工况

遵循“由简入繁”的原则，本研究首先选取缩尺模型的拉索刚度损伤工况进行分析。因为缩尺模型为稀索斜拉桥，一共只有16根斜拉索，故改变某几根拉索的刚度既不至于破坏结构，又能对结构性能产生明显的影响，易于识别。

由于结构在跨中的内力较大，贸然改变靠近跨中的斜拉索刚度有可能会对缩尺模型造成永久性损伤，故本试验方案选择同时改变结构右侧主跨靠近桥塔的一对拉索刚度。该拉索的位置如图2所示。

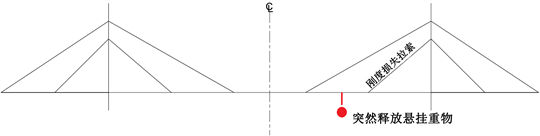
Figure 2. Location of the damaged cable

图2. 刚度损伤拉索的位置

为进一步探究拉索刚度对结构动力特性的影响，以该拉索的刚度损失比为参数，利用MATLAB有限元模型进行参数分析，结果如图3所示。限于篇幅，此处仅列出结构1阶竖弯模态的参数分析结果。

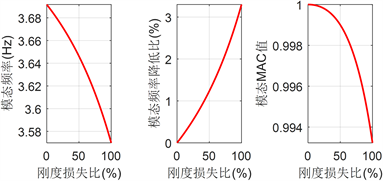
Figure 3. Parameter analysis of the 1^st mode

图3. 第1阶竖弯模态参数分析

图3中的MAC值为模态确认准则(Modal Assurance Criterion)，该参数的定义如下 [3] ：

$MAC\left({\varphi }_i^d,{\varphi }_i^u\right)=\frac{{\left|{\varphi }_i^{dT}{\varphi }_i^u\right|}^2}{{\varphi }_i^{dT}{\varphi }_i^d{\varphi }_i^{uT}{\varphi }_i^u}$ (1)

式中， ${\varphi }_i^d,{\varphi }_i^u$ 为损伤和非损伤状态下的结构第i阶振型，它表示振型相关图中最小二乘偏差的度量。

MAC是一个无量纲量，范围在0~1间变化，代表了两组模态向量之间的相关程度。当MAC = 1时，表明两组向量之间完全相关，即振型一致，单元无损伤；当MAC = 0时，表明两组向量之间完全无关，即这些单元不同于其他的单元，存在损伤。应用在结构损伤识别中，当MAC值接近于0或较小时，说明结构可能有损伤。

分析图3，可以发现结构的模态频率和振型MAC值均对拉索刚度损伤较为敏感。这样的结论是显然的，因为本模型一共只有16根拉索，同时改变其中两根拉索的刚度必然会造成结构整体刚度的明显改变。

3.3. 主梁刚度损伤工况

按照设计，本缩尺斜拉桥模型主梁主跨的左侧四分点位置被挖去了长10 mm的截面上缘，以模拟主梁的刚度损伤。刚度损伤的回复则通过安装带销钉的铝合金套筒实现。该损伤的位置如图4所示。

(a) 损伤位置 (b) 无损状态 (c) 损伤状态

Figure 4. Local damage of the beam

图4. 主梁的局部损伤

损伤前，主梁截面绕形心轴的竖向惯性矩为2118 mm⁴，损伤后，主梁截面绕新的形心轴的竖向惯性矩为939 mm⁴，刚度损失比为55.65%。

为进一步探究主梁局部刚度损伤对结构动力特性的影响，以该局部损伤单元的刚度损失比为参数，利用MATLAB有限元模型进行参数分析，结果如图5所示。由于在试验中观察到挖去主梁的截面上缘后，主梁刚度损伤局部没有产生不可恢复的变形，故在分析过程中，认为结构没有进入非线性，仍然采用线性方法分析。

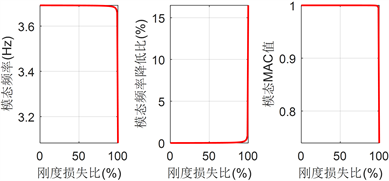
Figure 5. Parameter analysis of the 1^st mode

图5. 第1阶竖弯模态参数分析

分析图5，可以得到以下结论：

1) 刚度损失会导致结构的模态频率下降。这与结构动力学理论是一致的；

2) 结构频率和振型MAC值均对主梁局部刚度损伤非常不敏感。从图5中可以看出，主梁局部刚度损失80%以前，结构频率和和振型MAC值变化非常小。事实上，这样的结果是可以预料到的，因为结构频率和MAC值都是反映结构整体状态的参数，而主梁局部损伤的尺度很小，只有1 cm，仅占模型全长的1/600。

3) 结构频率和振型MAC值随着主梁局部刚度损伤比的增大非线性降低。主梁局部刚度损伤比越大，两个参数下降越快。当局部刚度损伤比达到95%以上时，这两个参数呈直线下降。这是因为过大的刚度损伤相当于改变了结构的边界条件，而结构的动力特性对边界条件更为敏感。

4. 损伤识别参数有效性分析

以上分析均基于数值计算，为进一步探究损伤识别参数的有效性，本研究进行了缩尺模型自由振动试验，利用试验采集到的结构加速度信号识别出结构模态，然后根据模态信息计算出损伤识别参数，验证这些参数的有效性。

4.1. 模态识别反问题

与通过有限元分析得到结构模态的模态分析正问题相对应，模态识别反问题是指通过分析结构的振动响应信号，得到结构模态的过程。按照既有的损伤识别思路，只有识别出蕴藏于振动响应数据中的结构模态参数，才能利用这些参数开展进一步的损伤识别与定位。

与结构振动模态相关的理论已经相当成熟，本文不再赘述。一般来说，模态参数通常包括：模态频率、模态振型、模态阻尼比、模态质量以及模态刚度 [4] 。其中最容易识别的是模态频率与模态振型，本文选取的正是这两个参数。常用的模态分析方法大致可分为频域法、时域法以及时频域法。其中频域法概念直观，由结构动力学中的振型分解法衍生而来，理论相对简单，本文最后采用频域法中的频域分解法识别结构的模态。

频域分解法是在峰值拾取法的基础上加以改进而得到的一种频域模态识别方法，该方法既具有简单快速的优点，又在处理密频或重频模态时有优势，精度更高 [5] 。

频域分解法的基本流程为，在各离散频率点上估计响应的自谱和互谱，形成功率谱矩阵如下 [6] ：

$\left[G_{yy}\left(\omega \right)\right]=\left[\begin{array}{cccc}PS{D}_{11}\left(\omega \right)& CS{D}_{12}\left(\omega \right)& \dots & CS{D}_{1n}\left(\omega \right)\\ CS{D}_{21}\left(\omega \right)& PS{D}_{22}\left(\omega \right)& \dots & CS{D}_{2n}\left(\omega \right)\\ \dots & \dots & \dots & \dots \\ CS{D}_{n1}\left(\omega \right)& CS{D}_{n2}\left(\omega \right)& \dots & PS{D}_{nn}\left(\omega \right)\end{array}\right]=USV$ (2)

上式中，PSD为自功率谱，CSD为互功率谱，U、V为奇异向量，S为奇异值矩阵。对功率谱矩阵进行奇异值分解，可以得到一组单自由度系统的功率谱，对应多个单自由度模态。对这些单自由度模态进行分析即可得到相应的模态参数。

图6展示了使用频域分解法从模型的自由振动加速度响应中识别出的结构模态形状。识别出的结构前3阶竖弯模态频率分别为3.86 Hz、6.30 Hz以及11.50 Hz，非常接近有限元模态分析得到的前3阶竖弯频率3.67 Hz、6.25 Hz以及11.80 Hz，说明模态识别结果是可靠的。

4.2. 拉索刚度损伤工况

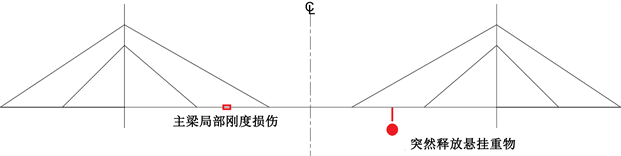
此工况下，直接拆除缩尺模型的一对斜拉索，然后在其主跨右侧四分点位置悬挂重物并突然释放(如果在跨中放置重物，无法激励主梁的二阶竖弯模态)，使模型自由振动。该工况的示意图如图2所示。采集结构自由振动的加速度信号，从加速度信号中识别模态参数，然后计算所选择的损伤识别参数。本研究选择的损伤识别参数为结构的模态频率、模态置信因子(MAC)以及模态坐标置信因子(COMAC)。其中模态置信因子在前文已有介绍，此处介绍模态坐标置信因子。

(a) 第1阶位移模态形状 (b) 第2阶位移模态形状 (c) 第3阶位移模态形状 (d) 第1阶应变模态形状 (e) 第2阶应变模态形状 (f) 第3阶应变模态形状

Figure 6. Recognized modal shapes

图6. 识别出的结构模态形状

模态坐标置信因子COMAC (Co-Ordinate Modal Assurance Criterion)指标定义如下 [7] ：

$COMAC\left(i\right)=\frac{{\left({\displaystyle {\sum }_{j=1}^N\left|{\varphi }_{i,j}^u{\varphi }_{i,j}^d\right|}\right)}^2}{{\displaystyle {\sum }_{j=1}^N{\left({\varphi }_{i,j}^u\right)}^2{\displaystyle {\sum }_{j=1}^N{\left({\varphi }_{i,j}^d\right)}^2}}}$ (3)

式中，点i处的两个状态u，d (完好和损伤)下的振型定义为： ${\varphi }^u,{\varphi }^d$ ；N为模态振型数。 ${\varphi }_{i,j}^u,{\varphi }_{i,j}^d$ 是指i点处分别在完好、损伤两种状态下，第j个振型的值。COMAC值是一个介于0~1之间的数值，该值越小，表明该测点的损伤越大。

计算刚度损伤工况下各阶模态的模态频率、MAC值以及COMAC值，结果如表2与表3所示。

Table 2. Modal frequency and MAC value

表2. 模态频率与MAC值

Table 3. COMAC value of displacement mode

表3. 位移模态的COMAC值

注：损伤拉索的索梁连接点X坐标为4.1 m。

分析上述模态识别结果与损伤指标计算结果，可以得到以下结论：

1) 由表2可以看出，拆除一对拉索会导致模型结构模态频率的明显下降。其中2阶和3阶频率下降百分比较高，因为被去掉的斜拉索的索梁连接点非常接近2阶以及3阶竖弯频率的峰值点，因此这两阶频率对该拉索的损伤更为敏感。

2) 由表2与表3可以看出，2阶模态的MAC值最小，测点a7位置的COMAC值最小，依据这一信息可以推断出损伤的位置大致出现在测点a7附近，

3) 虽然拆除一对拉索已经是相当显著的刚度损伤，但模态参数以及损伤指标的绝对变化仍然很小。实际工程中，温度变化、测量噪声等外界干扰造成的模态参数变化完全有可能盖过损伤所带来的模态参数变化。因此只能认为基于以上3种损伤识别参数，可以初步识别并定位出结构的显著损伤。

4.3. 主梁刚度损伤工况

此工况下，拆除缩尺模型主梁的局部刚度损伤构件，然后在其主跨右侧四分点位置悬挂重物并突然释放(如果在跨中放置重物，无法激励主梁的二阶竖弯模态)，使模型自由振动。该工况的示意图如图2所示。采集结构自由振动的加速度信号，从加速度信号中识别模态参数，然后计算所选择的损伤识别参数，如表4和表5所示。

Table 4. Modal frequency and MAC value

表4. 模态频率与MAC值

Table 5. COMAC value of displacement mode

表5. 位移模态的COMAC值

注：损伤拉索的索梁连接点X坐标为4.1m。

分析上述模态识别结果与损伤指标计算结果，可以发现，虽然主梁局部刚度损伤(局部截面刚度损失比55.65%)会造成结构模态的改变，但由于模态是反映结构整体性能的物理量，这样的改变是十分微弱的，即使是对损伤更为敏感的应变模态在损伤前后的变化亦很小。以上任何一个物理量都不能得出损伤识别与定位的明确信息，因此无法识别出主梁局部刚度损伤。

5. 结论

本文对一座6 m长缩尺斜拉桥模型进行了损伤识别试验，研究了模态频率、模态确认准则以及模态坐标置信因子三种基于结构振动模态的损伤识别方法，对于拉索刚度损伤和主梁刚度损伤两种损伤工况的识别效果，主要结论如下：

1) 损伤敏感性分析：以模态频率以及模态置信因子为指标，损伤刚度比为自变量，基于MATLAB平面有限元模型的损伤敏感性表明，缩尺模型的模态参数对拉索刚度损伤较敏感，对主梁局部刚度损伤不敏感。这是因为缩尺斜拉桥模型为稀索体系，单根拉索的刚度损伤对结构而言已经是显著的损伤，对比之下，主梁局部刚度损伤对结构整体而言只是微小的损伤。

2) 拉索显著刚度损伤识别：分析拆除一对拉索后的模型动力响应数据，可以发现三种损伤参数均有明显改变。根据这些变化，能够初步识别并定位损伤。

3) 主梁局部刚度损伤识别：分析拆除主梁局部刚度损伤构件后的模型动力响应数据，可以发现三种损伤参数几乎没有变化，无法由此识别并定位损伤。

基于结构模态参数的损伤识别方法难以有效识别出大型土木工程结构的局部损伤，而工程中关心的往往正是结构的局部损伤。因此可以认为，土木工程结构的损伤识别应不局限于常规方法，积极探索更高维度的解决途径。

致谢

本文得到国家重点研发计划(2017YFC1500603)与上海市科委(18DZ1201200)的资助。

NOTES

^*通讯作者。