校园一卡通消费行为的研究与分析

Research and Analysis of Campus Card Consumption Behavior

摘要: 项目通过R语言对校园卡消费信息记录的数据分析，提取统计量得到个人消费特征；依据消费特征和HCO算法建立预测校园内各消费点实时消费人数及工作人员分配模型。通过ARIMA模型预测消费特征，建立校园卡防盗刷模型和“余额–转账”模型，并进一步通过支持向量机和Apirori算法建立贫困生助学金、贷款项目审核分发模型。充分利用校园卡消费大数据，通过数学技术系统全面分析，构建各种为经济、安全服务的数学模型，提高了学生的生活质量并且产生一定的经济效益。

Abstract: The project uses R language to analyze the data of consumption information records of campus cards and extracts statistics to obtain individual consumption characteristics. According to con-sumption characteristics and HCO algorithm, it establishes a real-time consumption number pre-diction model and staff allocation model for each consumption point in campus. The ARIMA model is used to predict consumption characteristics, and the anti-theft brush model and the bal-ance-transfer model of campus cards are established. Furthermore, the support vector machine (SVM) and the Apirori algorithm are used to establish the auditing and distributing model of grants and loans for poor students. The paper makes full use of the big data of campus card consumption, through the comprehensive analysis of mathematical technology system, to build various mathematical models for economic and security services, improve students’ quality of life and produce certain economic benefits.

1. 引言

随着高校教育信息化的不断推进和重点部署建设，校园一卡通系统作为高校数字化校园建设的重要组成部分，对学校管理和决策支持发挥着重要作用。近些年应用功能不断拓展，一卡通系统每天产生大量流水数据，这些流水数据在一定程度上能够了解学生在校园内的数字轨迹，充分利用这些数据进行数据挖掘和分析，能够很好地为学校管理与决策提供有力的依据。

近几年国内已有很多高校意识到利用校园卡的相关数据进行某些方面的挖掘研究，例如武汉理工大学的学生经济状况与资助合理性评判系统 [1] 、复旦大学的签到查询系统、山东大学的贫困生评议等等，事实表明，利用校园卡数据分析挖掘方面的研究，对校园信息化建设的深入以及推动学校往更科学的管理方向上发展都是有相当的现实意义的。

我们希望通过数据挖掘方式提取校园卡数据中的学生消费特征，从而将其应用到校园卡防盗刷，余额–转账，餐厅人员调配等方面。通过对相关资料进行研究，我们决定采用数据挖掘算法以及优化算法来实现 [2] [3] [4] ，如支持向量机 [5] [6] [7] ，HCO算法等。模型的建立则参考人员调配方式模型、信用卡防盗刷等。通过建立合适模型并不断进行优化，最终得到可以用于实际的应用模型。

2. 数据预处理与特征提取

山东科技大学的校园卡系统中存储着全校师生大量的消费记录，我们通过联系学校校园卡工作处获得校园卡消费数据。然而原始数据由于门类过多，导致数据杂乱无章，很多有价值的信息都难以被发掘。因此，我们需要对原始数据进行清洗、整合和分类。我们将校园卡中由于系统问题导致的信息错误部分进行筛选剔除，将交易日期错误部分进行了改正。然后由于校园卡数据系统的消费数据和充值数据混杂，我们将数据进行分类处理。然后进一步将节假日和工作日数据进行分类，便于之后的讨论分析和研究。

数据经过清理和分类之后就可以进行个人消费特征分析了。通过R语言编程调用相关函数包对数据进行特征量分析，获得数据的各种统计学特征，如平均值，众数，极值等。

例如某同学的消费平均值为每日31.4，众数为4，极大值为28，小值为1.2，看出来此同学消费水平中等，经常一次购买4元的东西，最高一次花过25元，最低一次消费1.2元。消费次数为每日平均4.1次，可以推测此同学每天除了吃饭还会购买一些小零食或者水果一类的东西。以此类推可以将每个人的消费特征进行提取和归纳。个人消费特征归纳的角度是多元化的，我们可以通过每日消费每月消费之类的时间消费特征进行提取，也可以对同一pos机的消费次数进行分析，也就是根据地点进行消费特征提取，还可以根据消费金额在特定区间次数的频数进行提取。我们通过多元化的提取个人消费特征，从而全面的组成和分析个人消费习惯，进一步进行人员调度分配和个人校园卡防盗刷以及余额转账模型的构建。个人消费箱线图见图1。

Figure 1. One person consumption box line chart

图1. 某个人消费箱线图

除了个人消费特征提取，我们同样可以对群体消费特征进行提取。比如常去某一地点的人群有什么相同的消费特征，相同班级的学生在消费习惯上有什么共同点等等。

3. 消费行为分析

我们主要针对学校食堂的消费记录进行研究，抽样选取某学院大一至大四学生2017至2018全年的消费数据，将学生在食堂的消费数据按时间分为早餐、中餐和晚餐三类，对其中每一类，统计其在食堂的平均消费金额和消费金额标准差。

从表1中我们可以看出，四个年级早餐的平均消费均较低，标准差较小，个体消费变化差距不大，午餐和晚餐消费金额较大，其中晚餐消费金额最大，标准差也最大，说明晚餐时间学生在食堂的消费差异较大。从不同年级的学生消费情况来看，大一大二相较于大三大四消费的平均金额较小，标准差却相对较大，说明大一大二学生对于学校的食堂提供的食品刚开始购买，选择变化率更大，大三大四相较于大一大二学生对学校食堂菜品情况更加了解，所选菜品更为固定，而由于饮食观念的转变，高年级同学的消费金额相应有所增加，比较符合实际情况。

Table 1. Group consumption characteristics statistics

表1. 群体消费特征统计表

为将数据离散化便于进一步研究，于是将时刻进行划分，我们以30分钟为一次统计节点对消费记录进行划分统计，时刻划分表如表2。

我们按照上述对时间的划分规则绘制了校园卡食堂单日就餐峰值曲线图。

Table 2. Time division table

表2. 时间划分表

其中横坐标为时间，纵坐标为刷卡次数。由图2可以看出，学生单日就餐次数在11点40至13点20之间达到峰值，在下午5点20至6点20之间达到次峰值，而早餐时间的峰值要小于晚餐时间的峰值，由上述特征能够看出，学生在12点左右和6点左右到食堂就餐人次最多，而早餐时间人数过少可能是由于有大量学生没有吃早餐的习惯的缘故。

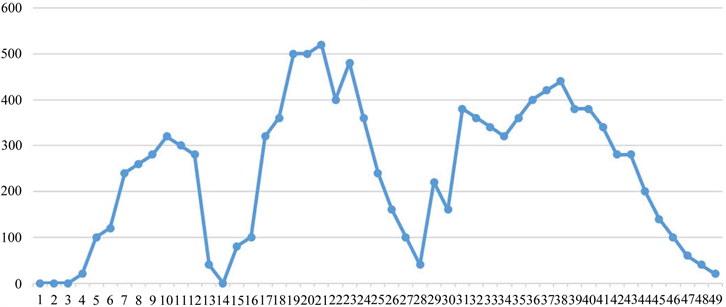
Figure 2. Canteen dining frequency trend chart

图2. 食堂就餐频次趋势图

考虑节假日和非节假日可能会对学生的消费状况产生影响，因此将所取原始数据样本按照不同消费地点划分为食堂消费、超市消费和其他消费三类，分别求其对应的月均刷卡频次和人均消费。

据表3可以看出在工作日期间，学生在食堂的刷卡频次明显多于节假日期间，而在超市和其他地点的刷卡频次节假日又明显多于工作日，从人均消费情况来看，假日期间三类地点的消费金额均多于工作日期间的消费金额。

Table 3. Location consumption statistics

表3. 地点消费统计表

4. 工作人员调度分派

通过上述对学生消费数据的分析，容易发现在某些时段食堂消费人数出现峰值平台期，即消费频次在某时刻达到峰值后，在之后的一段时间内，其频次一直维持在同一高度，我们考虑这种现象主要是由于食堂工作窗口过少，工作人员不足，从而导致了学生排队拥堵的现象。而在同一时刻，相较于食堂，超市的刷卡频次波动幅度并无如此剧烈，因此我们考虑从同一时间点交易频次低的消费地点分派人手到当前时刻交易频次较高的地点，以达到提高交易效率的目的。

针对本问题，我们参考对护士排班问题的解决方法构建模型 [8] [9]。采用APN的排班方式，即早班、白班和夜班的“三班制”模式，每个班次我们都定义为标准的8小时工作时间，且考虑轮休的情况，定义早班时间为0点至8点，白班时间为8点至16点，夜班时间为16点至24点，对这三种班次中的每一种，又按照2小时为一个单位进行班次细分。由于本文主要讨论的是消费地点的工作人员调度问题，因此将员工等级分为两类：工作时间未满一年的新员工，工作时间已满一年的熟练工，观察员工平时的工作效率，发现熟练工的工作效率大概是新员工的两倍，随着在校工作时间的增加，其相应的工资也相应增加。

由于排班问题面临的约束条件主要是指考虑员工健康的最长工作时间和满足企业的最短工作时长等的硬性约束以及符合尽量人性化等的软性约束，本文中的模型主要有以下7个约束条件：

每个员工每天只能值一次班；

所有员工不能在值夜班后的第二天值早班；

所有员工在连续两天夜班后休息一天；

新员工每个月至少排一次夜班；

在一个排班周期内，所有员工的最多天数不能超多规定上限；

在一个排班周期内，所有员工最短工作天数不能少于规定下限；

在一天中，每个员工在各个不同地点工作的总时间不能超过规定上线；

在一天中，每个员工在各个不同地点工作的总时间不能少于规定下线；

熟练工可以替代新员工所在的岗位，反之不行；

班后每一天中任何岗位的任何班次的员工数都大于等于学校的需求。

接下来用利用水纹循环优化算法(HCO)对问题进行求解。水纹循环优化算法是从水纹循环的自然现象引出的。其主要包括流动、渗透和蒸发与降水三种算子。在HCO算法中，流动算子是核心，其原理如下式所示。

$X_{try}=X_i+\left(X_j+X_i\right)\times rand\left(1,\text{Dimension}\right)$

其原理为让每个 $X_i$ 都尽量向一个较好的 $X_j$ 方向移动，若改变后的结果更差则放回原结果，知道达到终止条件时终止搜索。渗透算子是HCO中的第二个步骤，其对应公式为：

$X_{i,SD}=X_{i,SD}+\left(X_{i,SD}-X_{j,SD}\right)\times 2\times \left(rand\left(1,SD\right)-0.5\right)$

上式表示在渗透过程中，每个 $X_i$ 随机选择一个 $X_j$ 作为下一个探索点，在随机选择一些维度SD准备执行搜索。然后修改选定维度，使其远离 $X_j$ 点。渗透步骤可以更好地保持结果的多样性。蒸发和降水算子是HCO的第三个步骤，该算子使用两个规则来进行模拟：

在搜索范围内随机选取降水位置；

利用高斯分布移动到一个邻近的最优位置。

第一个规则可以有效保证结果的全局最优解性质，规则二可以大幅提高算法对局部最优解的搜索能力。

利用上述介绍的HCO算法及构造的约束条件与目标函数对问题进行求解，在模拟时取排班周期为7天，工作时间一年以上工作人员300人，工作时间不足一年的员工人数50人，蒸发概率取0.2，最大游动次数取2。

通过表4模拟计算，我们给出如下的人员调度改进意见：

Table 4. Staffing table

表4. 人员调配表

1) 节假日学生群体的就餐行为较少，食堂可适当地轮休，关闭部分售饭档口，减少工作人员，节约人力开支；

2) 节假日学生作息时间不规律，食堂应适当延长营业时间，为学生提供中高档菜品，适应学生群体的节假日消费行为特点；

3) 在11点40至12点40期间，食堂周边的超市应调拨其五分之一的员工去食堂进行工作，再加开两个窗口进行营业；

4) 在下午5点40至6点20之间，食堂周边的超市应调拨其八分之一的员工去食堂进行工作，再加开一个窗口进行营业；

5) 在午餐时间应多加派工作一年以上的熟练员工以提高工作效率；

6) 超市应在周末备足货源，为学生提供优质服务，干洗、数码冲印、洗浴、美发等服务业也是假日消费几项重要支出，因此上述行业应延长节假日的营业时间，为学生消费群体提供更好的优质服务。

5. 分析校园卡消费行为评定贫困生

5.1. 贫困生训练样本预处理

我们借鉴往年学校贫困生等级评价数据，筛选出贫困等级为特别困难和困难的学生，结合其对应的月消费数据，人工挑选出更有可能被人为评定为贫困生的50位学生的数据作为最初的训练样本数据，并从未被评为贫困生的学生消费数据中挑选消费过高的50位学生作为更不可能被人为评定为贫困生的数据训练样本。由于校园卡中数据过多不能直接利用，因此我们对数据进行了进一步的离散化处理，考虑到大学生的消费心理，从而选取如下几项指标作为贫困生评定指标：1) 早餐平均每餐消费额；2) 午餐平均每餐消费额；3) 晚餐平均每餐消费额；4) 平均每餐消费额；5) 月餐厅消费次数；6) 月总消费金额；7) (年花费总次数/年花费额) * 月平均消费次数。

5.2. 支持向量机分类模型

支持向量机是一种有指导的分类算法 [10] [11] ，支持向量机的主要思路是利用有限数量的样本观测来寻求待求的依赖关系，支持向量机方法是把样本点“升维”，即映射到高维空间甚至到无穷维空间，再在高维空间中采用处理线性问题的方法进行。支持向量机是从线性可分情况下提出的，对于n个线性可分的观测样本测样本 $\left(x_1,y_1\right),\cdots ,\left(x_i,y_i\right),\cdots ,\left(x_n,y_n\right)$ ， $x_i$ 属于 $R_n$ ， $y_i$ 属于 $\left\{-1,1\right\}$ 是类别符号。在n维空间中线性判别函数的一般形式为：

$g\left(x\right)=wx+b$

对于非线性的情况，通过非线性变换将输入变量x转化为某个高维特征空间中，然后在这个高维空间中求最优面，从而在高维空间可以利用内及运算对问题进行求解。通过引入核函数的方式，能够有效规避支持向量机高维空间的计算，并不显式的进行变换工作，把线性空间中的非线性问题映射到高维非线性空间中的线性问题，从而有效的解决非线性问题。射到高维非线性空间中的线性问题，从而自根本上解决非线性问题。

在对支持向量机进行模型构建时主要讨论以下两方面的构建：

1) 核函数的选取

选取不同的核函数能够形成不同的算法。通常用的核函数包括以下几种，多项式核函数、径向基核函数、sigmoid核函数等，线性核函数等。由于考虑到径向基核函数更适合于非线性分类的问题，且有较强的局部搜索分类能力，更适合对本文的问题进行求解，因此我们选用径向基核函数对所选指标集进行非线性多分类，其计算公式如下：

$K\left(x,y\right)=\exp \left\{-\gamma {\left|x-y\right|}^2\right\}$

2) 交叉验证选择最佳参数

惩罚参数c，核函数参数g的选取会一定程度上影响最终的实验结果，因此我们考虑如何对这两个参数进行最佳的设定 [12]。关于支持向量机的参数优化选取，国际上没有公认的统一的最好的方法，较为简单的方法为让c与g在一个范围内取一系列离散值，再分别检验取最优，然而此种方法在不知道此时标签的情况下无法使用且会出现多组最有参数组合的情况。因此，本文采用交叉验证(CV)的方法对这两个进行标定，其采用的方法为：选取能够达到最高验证分类准确率中参数c最小的那组c和g作为最佳参数，如果对应最小的c有多组g，就选取搜索到的第一组c和g作为最佳的参数。采用这种方法能够一定程度上解决上述提到的问题。

利用上文预先挑选出来的100组数据集对应的7项指标，对以构建的多分类支持向量机进行训练，再对余下测试数据的相应指标进行分类，完成对学生贫困生评定的首次划分。

5.3. 关联规则Aprior算法

关联分析是数据挖掘的一个重要方法 [13] ，关联是指两个或者多个变量之间存在的某种规律性。关联规则是寻找在同一事件中出现不同项目的相关性，关联分析是挖掘关联规则的过程。最经典的关联规则挖掘算法是Apriori算法，该算法使用频繁集的先验性质，主要进行逐层搜索的一种迭代方法，其中m项集用于构建m + 1候选项集。算法的实施步骤如下：首先，扫描事务数据库，累计每个项的出现的次数，找出大于等于min-sup的项，构建频繁1项集的集合。该集合记为L1。然后，从频繁1项集扩展候选2项集，找出大于等于最小值支持度的频繁2项集，记为L2，从频繁2项集扩展候选3项集，找出频繁3项集的集合L3，循环进行，直到找到出频繁m项集。找出每个频繁项集都需要一次完整的数据库扫描。

关联规则的几个基本的定义如下所示：

(1) 给定一个交易集D，挖掘关联规则问题就是产生支持度和可信度分别大于用户给定的最小支持度 $\left(\min \sup p\right)$ 和最小可信度 $\left(\min conf\right)$ 的关联规则。

(2) 关联规则的支持度(support和信任度(confidence)是两个用来度量有关规则趣味性的方法。它们分别描述了一个被挖掘出的关联规则的有用性及确定性。

(3) 支持度是指事务集D中包含了的A推导出B的模式在整个问题领域出现的概率。即 $\sup port\left(X\ge Y\right)$ 等于同时包含项目集X和Y的交易数/总交易数。

(4) 置信度是指D中包含X的事务同时也包含Y的百分比。即 $\text{confidence}\left(X\ge Y\right)$ 等于同时购买商品X和Y的交易数/购买商品。

利用关联规则Aprior算法实现分类的关联规则分析，以关联规则的频繁项集为参照，设定最小支持度阈值和最小置信度阈值，根据每次计算得到的支持度与置信度的数值，筛选支持向量机分类后的总样本数据中对应的支持度和置信度都大于对应阈值的数据项，从而得到两个类别的频繁模式过滤原始样本，再分别从中优选支持向量机分类样本对支持向量机模型重新进行训练，以对提高分类的科学性。

贫困生评定模型的步骤如下所示：

对原始数据进行处理，统计评价指标。

结合历史评定数据和消费记录人工选定原始训练样本。

对以构建的多分类支持向机进行训练。

用训练好的支持向量机分类模型，对测试数据集进行分类。

利用两个类别的频繁模式过滤原始样本，从原始样本中选择更有代表性的数据重新构建训练样本。

反馈给(1)循环进行模型修正，直至分类差别小于指定的阀值。

流程图见图3。

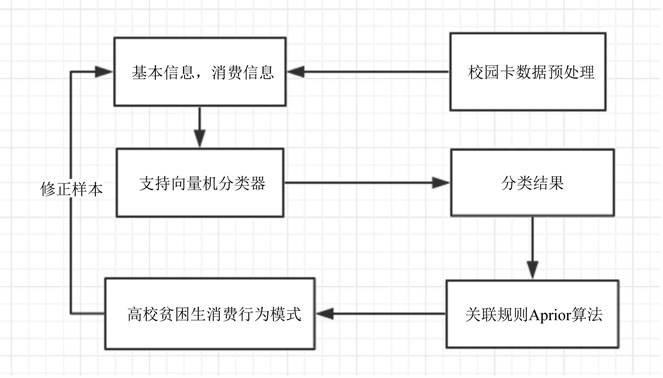
Figure 3. Data preprocessing flowchart

图3. 数据预处理流程图

最后得出模型的分类结果如图4。

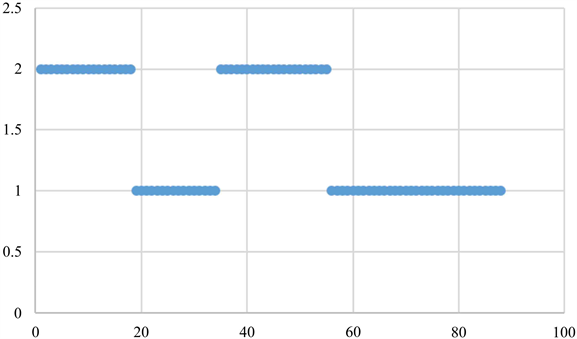
Figure 4. Test result classification chart

图4. 测试结果分类图

通过图4结果可以看出本文中模型的评价结果与现有的贫困生评价结果对于大部分学生的评定较为相近，但有少部分被本模型评定为非贫困生的学生在人工评定时被评为贫困生，需结合对相应同学的家庭生活情况进行进一步考察。

6. 防盗刷和校园卡圈存

本文主要从个人的消费金额和消费金额与地点的关联度来进行分析是否当学生的校园卡被盗刷以及是否需要进行校园卡圈存。

1) 消费金额分析

统计全年工作日个人每天的消费金额，并利用matlab绘制其消费金额随时间的变化的时间序列图。

通过图5和图6可以发现，当前选取的学生的消费行为有明显的周期性变化，基本上以一周为一个周期，其全年的消费规律在两个不同的学期之间存在较大差异，在每个学期里有明显的周期性规律，且在上半学期基本上在周二和周四达到一周的消费高峰，在下半学期，基本上在周一和周四达到消费高峰，全年的消费低谷基本上均在周五至周日这段时间内，这一结果可能和学校的课程时间安排密切相关，该生可能在周一周二和周四的课程较多，只能在校用餐，而到周五和周末时，由于课程安排较少，可能选择回家用餐获外出用餐。在进行了以上的初步分析后，我们为更加精确的分析每个学生的个人消费金额特征，引入ARIMA乘机季节模型，对学生的消费数据进行分析。

ARIMA乘机季节模型是随机季节模型与ARIMA模型的结合。假定X_t为某时间序列第t个时间间隔的观测值，统计学上纯 $\text{ARIMA}\left(p,d,q\right)$ 模型记作：

$\Phi \left(B\right){\nabla }^d{X}_t=\Theta \left(B\right){\epsilon }_t$

其中t代表时间，X_t代表相应序列，B是后移算子， $\nabla =\text{1}-B$ ，p，d，q分别表示自回归阶数，查分阶数和移动平均阶数； $\Phi \left(B\right)$ 表示自回归算子； $\Theta \left(B\right)$ 表示华东平移算子。

一个阶数为 $\left(p,d,q\right)\times \left(P,D,Q\right)s$ 的乘机季节模型可表示为：

Figure 5. Timing chart of someone’s consumption in the last semester

图5. 上学期某人消费时序图

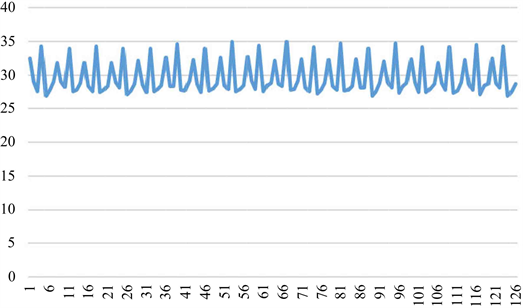
Figure 6. Timing chart of someone’s consumption in the next semester

图6. 下学期某人消费时序图

$\Phi \left(B\right)U\left(B^S\right){\nabla }^d{\nabla }_S^D{X}_t=V\left(B^S\right)\Theta \left(B\right){\epsilon }_t$

其中 $\Phi \left(B\right)=1-{\varphi }_{1}B-{\varphi }_2{B}^2-\cdots -{\varphi }_p{B}^p$ ， $\Theta \left(B\right)=1-{\theta }_{1}B-{\theta }_2{B}^2-\cdots -{\theta }_q{B}^q$ ；

$U\left(B^S\right)=1-u_1{B}^S-u_2{B}^{2S}-\cdots -u_P{B}^{PS}$ ， $V\left(B^S\right)=1-{\nu }_1{B}^S-{\nu }_2{B}^{2S}-\cdots -{\nu }_Q{B}^{QS}$ 。

${\epsilon }_t$ 代表独立挠动或随机误差， $s$ 是一个季节循环中观测的个数， $\Phi \left(B\right){\nabla }^d{X}_t$ 表示同一周期内不同周期点的相关关系， $U\left(B^S\right){\nabla }_S^D$ 则描述了不同周期的同一周期点上的相关关系，二者结合便同时刻画了两个因数的作用。当 $P=D=Q=0$ 时该模型便是一般的 $\text{ARIMA}$ 模型 [14]。

ARIMA建模与预测包含4个步骤：

序列平稳化处理。如果序列是非平稳的, 可以通过差分变化使其满足平稳性条件。

模型识别。主要通过自相关系数和偏自相关系数来确定模型的阶数p和q。

参数估计和模型诊断。估计模型的参数，并检验(包括参数的显著性检验和残差的随机性检验)，然后判断所建模型是否可取。

利用所选取合适参数的模型进行预测 [15]。

此处以某学生2017至2018学年下半学期的消费金额数据为例，利用MATLAB建立时间序列模型。首先对所取数据进行差分，判断其是否平稳性，得到差分图。

从图7可以看出，在去除节假日的消费记录之后，其余的数据比较平稳，有利于利用ARIMA模型进行预测。其自相关系数图如图8所示。

Figure 7. Data difference map

图7. 数据差分图

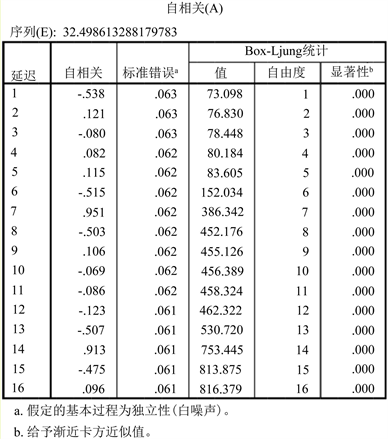
Figure 8. Autocorrelation coefficient map

图8. 自相关系数图

根据上述结果确定ARIMA的参数p，d，q的数值，并绘制相应的预测曲线如图9所示：

从图9预测结果可以看出模型预测结果与学生实际的消费规律比较相近。接下来对预测结果进行检验，做出图9的ACF图像。

Figure 9. Forecast graph

图9. 预测曲线图

从图10中可知，残差没有明显的自相关性，因此该模型参数的选取较为合理。

Figure 10. ACF analysis image

图10. ACF分析图像

消费–地点关联性分析

考虑每个人的消费方式会随着消费地点而不同，因此我们依此统计每天对应不同地点的消费金额，此处将消费地点划分为以下几类：食堂、超市、机房、其他。利用前文介绍的关联规则模型，计算每个学生消费金额和其消费地点的支持度和置信度，用以确定学生每日的消费金额与地点、时间的最低对应阈值。

3) 盗刷行为及圈存行为出发判定

当预测结果与实际交易流水进行比较出现较大差异时，则大概率判断当前为消费异常行为。对新的消费数据计其相应的支持度和置信度，若小于对应的最低阈值时，则可大概率判断当前消费行为出现异常，存在被盗刷的情况。结合上述两种判断方法，当被上述两种判别方法中至少一种方法判断为异常消费时，则通过对学生发送通知或信息验证的方式进行消费确认，根据确认结果利用ARIMA乘机季节模型和关联规则重新修正原有判别要求。从而完成对校园卡的防盗刷实时监控机制。

通过计算分析得到每个学生的最短消费周期，“转账触发线”以及转账金额，若当前校园卡内金额小于利用ARIMA乘机季节模型预测的下一周期的金额，则启动校园卡圈存机制，转入金额数至满足下一消费周期的预测可能消费金额为止。

4) 模型检验

本文利用MATLAB软件，随机产生盗刷行为以及在现有数据噪声的方式生成新的正常交易数据，对上述模型进行模拟，得到判定结果如表5所示。

通过表5结果我们可以看出模型的判别效果较好，能够有效的判别异常消费行为，误判率较低，对小金额的盗刷行为判别较为灵敏。整个建模流程图见图11。

Table 5. Simulation result table

表5. 模拟结果表

Figure 11. Analysis algorithm flow chart

图11. 分析算法流程图

7. 结论

本文建立了系统科学全面的数据分析算法模型，利用校园卡中的数据得到个人消费特征，从一个全新的角度了解当今大学生的消费特点。我们利用ARIMA模型将学生消费特征与校园中消费点工作人员数量调配相联系，建立实时人员调度模型，提高了目前消费点的服务效率与服务质量。利用支持向量机和Aprior算法建立审核贫困助学金评定模型，使其更加合理和高效。利用学生消费特征和ARIMA方法，建立小金额防盗刷模型，识别小金额支付异常现象，并给用户及时提供校园卡盗刷信息反馈。将学生消费特征作为影响因素，根据每个人的不同消费特征，设立个人特有的“转账触发线”，以满足不同人群的消费需求。