基于VB和FORTRAN混合编程的时程曲线绘制

Time History Curve Drawing Based on Mixed Programming of VB and FORTRAN

摘要: 大体积混凝土坝施工仿真常常历时数年，需要知道任意给定点的物理量值在某一时间段内的变化情况。为此，采用VB和Fortran混合编程的方法，以动态链接库DLL文件作接口，结合VB时程曲线绘制方法，研制了混凝土坝时程曲线显示模块，作为后处理软件的一部分。该模块可以高效显示混凝土坝任意给定点的物理量值在某一时间段内的变化情况。

Abstract: The construction simulation of large-volume concrete dams often lasts for several years, and it is necessary to know the changes of the physical quantity of any given point within a certain period of time. For this, using VB and FORTRAN mixed programming method, using dynamic link library DLL file as interface, combined with VB time history curve drawing method, concrete dam time-history curve display module is developed, as part of post-processing software. The module can efficiently display the change of the physical quantity of any given point of the concrete dam within a certain period of time.

1. 引言

等值线和云图都是结构在选定的一个时间点某物理量值的分布图，大体积混凝土坝施工仿真常常历时数年，需要知道任意给定点的物理量值在某一时间段内的变化情况，即时间历程曲线。目前，等值线和云图已有成熟算法，多数后处理软件均具有该功能，而对任意点的时程曲线绘制研究较少，难以满足大体积混凝土坝施工仿真后处理要求。为此，本文研究了从庞大的有限元结果中提取任意给定点的物理量值的关键技术：等参逆变换，采用Taylor展开的线性项进行的逆变换算法编制了Fortran语言的计算程序，实现了任意给定点的结果数据提取。研究图形显示所需的坐标轴自动刻度算法，提出了更为高效简洁的算法。采用VB和Fortran混合编程的方法，以动态链接库DLL文件作接口，结合VB时程曲线绘制方法，研制了混凝土坝时程曲线显示模块。该模块已形成软件，并在大型碾压混凝土坝温度场及温度应力施工仿真中得到应用。

2. 等参逆变换算法

等参单元是目前有限元软件中最常用的单元，在如ANSYS，ABAQUS，ADINA，NASTRAN 等通用商业软件中具有重要地位，广泛应用在各种十分复杂的工程分析项目中。该变换的特点在于仅能列出正变换的显式 ，而不能列出其逆变换的显式，由于该单元所有矩阵的推演都是在局部坐标系中进行的，一般可以避免逆变换。然而，在某些特殊的情况下，这样的逆变换是无法避免的。例如，在绘制时程曲线时，用户输入的都是任意点整体坐标，因为有限元计算所得结果都是节点值，所以对非节点的点必须进行坐标逆变换求出局部坐标以后再求该点的物理量值。

对于等参逆变换，国内外学者已进行过研究。钱向东、徐燕萍等人运用Taylor级数展开的方法进行了迭代求解 [1] [2] ；朱以文等人通过求解9次方程来求解局部坐标 [3] ；包劲青等人采用几何二分法 [4] ，避免了求解高维高阶的非线性方程组，但需要修正，以消除畸形单元对所求结果的影响；Murti等人提出过一般性逆变换算法 [5] ，但过于复杂，实际应用较少。本文采用文献 [1] 中的用Taylor展开的线性项进行的逆变换算法，该算法作了较大的简化，迭代格式简单明确，有利于程序实现。

如图1所示，对整体坐标中一点 $P\left(x,y,z\right)$ ，其局部坐标 $\left(\xi ,\eta ,\zeta \right)$ 应符合下式

$\begin{array}{l}x={\displaystyle \underset{i=1}{\overset{n}{\sum }}{N}_i\left(\xi ,\eta ,\zeta \right)x_i}\\ y={\displaystyle \underset{i=1}{\overset{n}{\sum }}{N}_i\left(\xi ,\eta ,\zeta \right)y_i}\\ z={\displaystyle \underset{i=1}{\overset{n}{\sum }}{N}_i\left(\xi ,\eta ,\zeta \right)z_i}\end{array}$ (1)

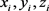式中，为三维等参单元的形函数矩阵，为单元节点坐标，n为单元节点数。

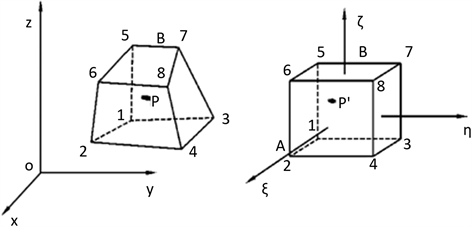
Figure 1. Isoparametric element with 8 nodes in space

图1. 空间八节点等参单元

将方程(1)的 $\left(x,y,z\right)$ 在点 $\left({\xi }_0,{\eta }_0,{\zeta }_0\right)$ 进行Taylor级数展开，仅保留线性项，其矩阵形式表示为

$\tilde{x}\approx {\tilde{x}}_0+{\tilde{J}}_0^{\text{T}}\left(\tilde{\xi }-{\tilde{\xi }}_0\right)$ (2)

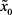式中，为对应于 ${\tilde{\xi }}_0$ 的整体坐标， $\tilde{\xi }$ 为对应于的局部坐标， ${\tilde{J}}_0^{\text{T}}$ 为处的Jacobi矩阵的转置矩阵。由式(1)可直接解出

$\tilde{\xi }\approx {\tilde{\xi }}_0+{\left[{\tilde{J}}_0^{\text{T}}\right]}^{-1}\left(\tilde{x}-{\tilde{x}}_0\right)$ (3)

式中，为 ${\tilde{\xi }}_0$ 处的Jacobi矩阵转置矩阵的逆矩阵。由式(2)可以建立求解等参单元内任意点 ${\tilde{x}}_p$ 所对应的局部坐标 ${\tilde{\xi }}_p$ 的迭代公式

${\tilde{\xi }}_{k+!}\approx {\tilde{\xi }}_k+{\left[{\tilde{J}}_k^{\text{T}}\right]}^{-1}\left({\tilde{x}}_p-{\tilde{x}}_k\right)$ (4)

其中 ${\tilde{\xi }}_k$ 表示 ${\tilde{\xi }}_p$ 的第k次近似值， ${\tilde{x}}_k$ 为 ${\tilde{\xi }}_k$ 对应的整体坐标向量， ${\left[{\tilde{J}}_k^{\text{T}}\right]}^{-1}$ 为 ${\tilde{\xi }}_k$ 处的Jacobi矩阵转置矩阵的逆矩阵。

3. 自动刻度算法

时程曲线绘制时，因数据的范围是不固定的，故不能够在程序编制时就确定下来坐标轴刻度。若利用程序根据数据的范围动态调整坐标轴刻度，则设置的刻度很可能不符合人们的读图习惯，所以研究坐标轴刻度标定的程序化是很有必要和意义的。

费海涛、朱连章等人提出的坐标轴刻度规范化处理算法 [6] [7] ，使用提供的坐标起点、终点和刻度数推导出了刻度的步长、起点和终点的规范化计算公式，并编制了根据数据变化范围动态设置坐标轴刻度的通用程序。但该算法还有一些不足之处，利用新确定的单位长度、最小刻度值、最大刻度值计算出来的新刻度数，可能与原刻度数并不相等，于是则须在步长不变的情况下重新修正最小、 最大刻度值，故增大了计算量。本文提出了确定坐标轴刻度的简易算法，克服了上述算法存在的不足之处。

坐标轴刻度规范化标定关键在于步长的规范化，因为只要步长确定了最大刻度最小刻度只需根据步长略微调整即可，而一旦这三个量定了以后刻度数就是确定的了。符合人们读图习惯的步长一般为0.1、0.2、0.25、0.5、1，或者是这些步长的下一个或多个数量级的数据。设变量的最大值最小值分别为 $v_{\max }$ 和 $v_{\min }$ ，则刻度区间为 $\Delta v=v_{\max }-v_{\min }$ 。利用科学记数法 $\Delta v$ 可以表示为

$\Delta v=t\cdot {10}^{\lambda }$ (5)

式中 $t\in \left[1,10\right)$ 。

至此，我们已将普通问题转化为已知的特定问题，即根据t值来从集合 $\left\{0.1,0.2,0.25,0.5,1\right\}$ 中选定步长 $t_{step}$ ，则原问题规范化步长为

$v_{step}=t_{step}\cdot {10}^{\lambda }$ (6)

求出规范步长 $v_{step}$ 以后，利用 $$ 来对原始最大最小值 $$ 和 $v_{\min }$ 进行调整，即求刻度的起点和终点。

$n\cdot v_{step}\le v_{\min }$ $n\in N$ (7)

$m\cdot v_{step}\ge v_{\max }$ $m\in N$ (8)

分析可知，求出满足式(7)的n的最大值 $n_0$ ，和满足式(8)的m的最小值 $m_0$ ，也就求出了刻度的起点和终点，分别为 $n_0\cdot v_{step}$ 和 $m_0\cdot v_{step}$ 。而刻度数为

$k=m_0-n_0$ (9)

综上可见，本文算法简洁高效，便于程序实现，省去了文 [7] 中的反复修正的繁琐过程。

4. VB和Fortran混合编程技术

目前，VB与Fortran混合编程主要方法有两种 [8] [9] [10] ，即VB直接调用可执行文件(利用Shell函数调用Fortran程序的可执行文件)和利用动态链接库DLL格式文件与Fortran混合编程。其中，动态链接库因其具有静态链接库的功能，并且有节约内存和硬盘空间等优点而被广泛应用。本文采用动态链接库方法进行VB和Fortran的混合编程。

Fortran建立动态链接库方法如下：首先建立一个类型为 Dynamic Link Library的New Project Work space，然后将一个只含有函数或子程序的Fortran程序加入到Project 中，编译通过即可生成动态链接库。在Fortran程序中，被调用的函数或子程序必须予以声明，声明语法如下：

! MS $ ATTRIBUTES DLLEXPORT:: Name

ATTRIBUTES是Fortran Power Station 4.0中的元命令，用于声明微软扩展属性。DLLEX-PORT是上述属性之一，它的作用是声明该函数或子程序能被其他程序或动态链接库调用。Name为函数或子程序名。该语句需放在程序的变量声明处。

利用VB 调用Fortran动态链接库时，首先在VB的模块级或相应的窗体中对被调用的动态链接库进行声明，语法如下：

Public Declare Sub Name lib libname Alias aliasname [(arglist)]

Declare语句是用于声明对动态链接库中外部过程的引用。Public用于声明在所有模块中对所有其他过程均合法的过程；libname指明动态链接库名及其路径；aliasname指明被调用的过程在动态链接库中的别名，一般为_Name@ n，n表示栈的大小，它是4的倍数；arglist为参数的变量清单。声明之后，VB 中使用Call语句调用动态链接库中的函数或子程序，调用语句如下：Call Name(arglist)，Name的意义同上。

5. 工程应用

某碾压混凝土重力坝坝顶长1250 m，最大坝高159 m。对于溢流坝段，每个坝段厚为20 m，考虑溢流坝段对称，取一半分析，网格剖分采用8节点六面体等参元模型，地基范围在水平方向和深度方向各取100 m。有限元模型中共分7344个单元，9725个结点，如图2所示。利用温度场及温度应力三维有限元计算程序进行仿真计算。利用本文所研制的软件对其计算结果进行可视化处理，见图3和图4。利用本软件可以很方便地得到温度及应力等物理量值随时间变化的曲线，对混凝土大坝的温控防裂提供可靠信息和帮助。

Figure 2. Finite element model

图2. 有限元模型图

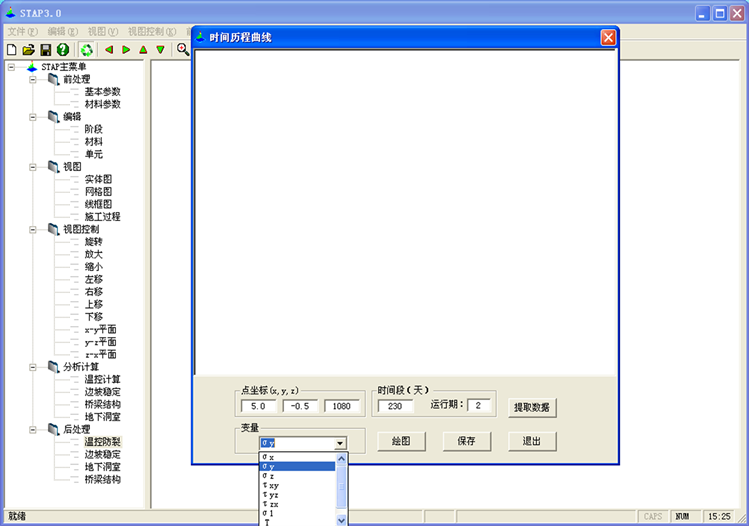
Figure 3. Time history curve operation interface

图3. 时程线操作界面

如图3所示，首先输入绘制点的三个坐标分量值，然后输入时间段（前多少天）及运行期，点击“提取数据”按钮，VB程序调用Fortran动态链接库，Fortran程序利用等参元逆变换算法得到点的局部坐标，并计算这一点在这一时段的相应物理量值返回给VB程序。提取数据成功以后选取所要绘制的物理量并点击“绘图”，VB程序对Fortran动态链接库计算得到的物理量值利用自动刻度算法绘制出时程曲线。图4是点(5.0, −0.5, 1080)前230天的温度变化曲线。

6. 结论

本文提出的自动坐标刻度算法简洁高效，并且便于程序实现，省去了反复修正的繁琐过程。

Figure 4. Time history curve of temperature

图4. 温度时程曲线

采用VB与Fortran混合编程的方法，以动态链接库DLL文件作接口，开发出混凝土坝时程曲线绘制模块。该模块充分利用了Fortran语言的科学计算能力和VB开发界面及图形绘制的功能，实现了程序资源的共享，提高了程序的工作效率，并具有友好的程序界面。

参考文献