1. 引言
金融系统是一个多要素且极复杂的非线性系统。由于参数的改变可能使系统出现混沌状态,使得很多金融问题变得更加复杂,如金融市场出现停滞、失控甚至引发金融危机等现象。非线性经济动力学理论分析有助于预测和解决经济市场中存在的一些非线性问题,对于非线性经济学领域的研究具有重要的理论和实践意义。众所周知,不受控制的随机扰动是任何实际系统的必然属性,特别是在经济学中,即使是非线性系统中的弱噪声也能显著地改变其动态特性。因此,分析随机扰动的影响是现代经济动力学理论中的一个具有挑战性的问题。加入随机干扰可能会引发各种现象,例如规则与混沌的相互转换、随机分岔、随机共振以及噪声诱导转换 [1]。对于吸引子附近的概率分布,KFP方程给出了最详细的概率描述。然而,即使是对于最简单的情况,直接使用这个方程也是非常困难的。我们采用拟势函数的小噪声分布密度,根据其渐进分析 [2]。利用随机灵敏度函数(SSF)方法,构造连续和离散时间系统的随机吸引子的概率描述。
一维的带有切线和危机分岔离散时间系统中应用SSF技术,通过置信区间给出了随机平衡中随机状态的偏差的构造性描述。置信区间大小由噪声强度、随机灵敏度值和基准概率定义。对引发间歇性的参数进行分析,得到相应噪声强度阈值 [3] [4]。
对二维的卡尔多商业离散系统和Brusselater系统的研究广泛地应用了SSF技术,充分研究了其系统状态的相互转化 [5] [6] [7]。
在三维情形,当随机Lorenz系统和Rossler系统出现倍周期分岔时,利用SSF技术有效分析了其附近的混沌现象 [8] [9] [10]。然而在金融模型中还未应用过这个方法对吸引子进行概率描述,本文中将SSF技术应用到改进的三维金融模型中,利用可达性条件设计控制器来控制随机吸引子到平衡点。
2. 一类确定性金融系统的参数分析
2.1. 一类金融系统的改进
本文研究如下金融系统 [11] :
(1)
其中
代表利率,
代表投资需求,
代表价格指数,
表示储蓄量,
表示单位投资成本,
表示商品需求弹性。经过研究以及数值模拟发现,当
时,金融系统出现混沌吸引子,能够反映经济的一些变化规律,在系统(1)的基础上,发现影响利率变化的因素除了投资需求、价格指数外,还与平均利润率有关,且平均利润率与利率成正比例关系。考虑到利率
变化与物价价格有可能会出现弹性正比关系,并发现调整弹性系数,也能使金融系统出现的混沌状态消失,达到稳定状态,或周期状态。对系统(1)中第一个方程做了改进,即在利率
原始变化中,于价格指数
前引入权值参数
,构造如下改进的金融混沌系统:
(2)
2.2. 确定性系统局部稳定性与分岔
令系统(2)左端为零,经过计算可以得到:当
时,系统(2)有唯一平衡点;当
时,系统(2)有三个平衡点,分别为
2.2.1. 平衡点E1的pitchfork分岔与Hopf分岔
将平衡点
代入Jacobi矩阵可以得到特征方程
根据Routh-Hurwitz定理,结合用中心流行定理与分岔的判定定理,可以得到如下结论。
定理1:当
且
时,金融系统在平衡点
处经历pitchfork分岔。即当
且
时,系统(2)有唯一平衡点 ,且此时平衡点
为局部渐进稳定的;当
且
时,系统(2)增加两个稳定平衡点
和
,即系统(2)有三个平衡点,此时平衡点
由稳定变为不稳定。
,且此时平衡点
为局部渐进稳定的;当
且
时,系统(2)增加两个稳定平衡点
和
,即系统(2)有三个平衡点,此时平衡点
由稳定变为不稳定。
定理2:当
且
时,系统(2)在平衡点
处经历Hopf分岔。
为了验证定理1和定理2的理论结果,现取参数a = 9.6,b = 0.1,k = 0.5,计算可得 ;当
,
,所以,当
时满足定理1中
且
的条件,平衡点
是局部稳定,
时,系统有两个稳定的平衡点;如果
;当
,
,所以,当
时满足定理1中
且
的条件,平衡点
是局部稳定,
时,系统有两个稳定的平衡点;如果 ,
,
不变,取
时,金融系统(2)在平衡点
经历Hopf分岔,出现周期轨。
,
,
不变,取
时,金融系统(2)在平衡点
经历Hopf分岔,出现周期轨。
2.2.2. 平衡点E2和E3的Hopf分岔
将平衡点
和
代入Jacobi矩阵,可得特征方程
其中,
。
由Routh-Hurwitz定理和Hopf分岔定理可知:
定理3:当
(或
)时,
和
局部渐进稳定。当
,金融系统(2)在
和
处同时经历Hopf分岔。其中
固参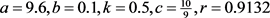 ,取初值
,取初值
 ,确定性系统吸引子的轨迹如图1所示。
,确定性系统吸引子的轨迹如图1所示。

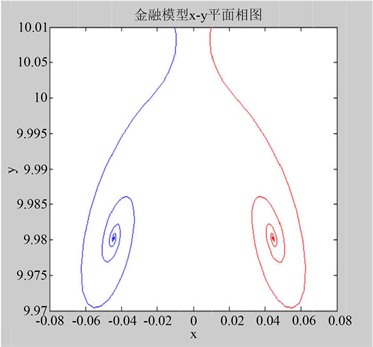


Figure 1. Deterministic system attractor
图1. 确定系系统吸引子
由图1可以看到,当
时,系统出现两个稳定的平衡点,当
时,系统在平衡点
和
处同时发生Hopf分岔形成了两个周期轨,当
时,系统出现混沌吸引子,当
时,系统只有一个稳定的平衡点。
3. 随机平衡点的灵敏度
在系统(2)中加入标准的维纳过程可以得到以下随机系统
(3)
在系统(3)中,
为噪声强度,
为标准的维纳过程。
由图2和图1对比可以看出随机系统的轨迹离开确定吸引子,但是在其周围形成随机吸引子,一般随机可能会引起系统状态的转换。比如当时,可以看出系统有从周期态向混沌态过渡的趋势。



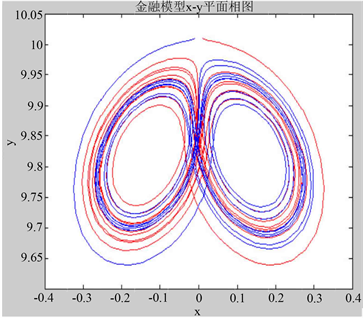
Figure 2. Attractor of stochastic financial system (
)
图2. 随机金融系统的随机吸引子(
)
将系统(3)表为如下形式:
(4)
是一个3维向量,
是一个3维维纳过程,
是强度参数。
在本文中我们取
当
,假设系统(4)有指数稳定的平衡点,这样随机系统(4)的随机轨迹就会离开平衡位置并在其周围形成带有平稳概率分布
的随机吸引子(如图2),
是Fokker-Planck方程的解,但是即使在二维的情况下,这个方程也很难获得解析解。对于小噪声,我们可以得到
的近似
,基于拟势函数 [12]。
函数 在平衡点附近有指数的高斯近似
。
在平衡点附近有指数的高斯近似
。
其中拟势函数
,矩阵
是随机系统的随机灵敏度矩阵。矩阵
是正定对称矩阵,且是下面矩阵方程的解 [13]
(5)
在(5)中,
,对于指数稳定平衡点
,矩阵
的所有特征值
满足
,上述矩阵方程有唯一解。由高斯近似可以得到:
的迹越小,
越小,则
越小,所以随机轨迹越趋近于平衡位置。反之
的迹越大,则随机轨迹越远离平衡位置。由矩阵方程(5)可以解出随机灵敏度矩阵,当
时,矩阵为
定义
,我们将
作为衡量随机灵感度的指标,
,显然这个值非常大,这也是随机轨迹紊乱的原因(如图2),为了平衡随机系统中的紊乱轨迹并抑制其混沌状态,下一节我们设计一类控制器来控制随机金融系统,并计算出控制器的随机灵敏度矩阵。
4. 随机系统的稳定控制
考虑随机受控金融系统
(6)
我们采用常规反馈控制器 ,
,
即
。
由于在随机系统中无法直接描述概率分布,我们引入第一近似系统 [10] ,系统(4)的第一近似系统为
其中
。
所以对应于系统(6)的第一近似系统为
其中
。
因为系统(4)的随机灵敏度矩阵由矩阵方程(5)解出,要解系统(6)的随机灵敏度矩阵
,由方程(5)可以推出
(7)
是随机灵敏度矩阵的集合,其中元素满足对称和正定性。
是矩阵A的特征值。
定义1:充分随机可控:如果
,那么系统(6)是充分随机可控的。
定义2:可达:如果对于一些
满足
成立,对于系统(6)来说,元素
可达。
对于本文所研究的系统,
,那么系统(6)就不是充分随机可控的,这样就需要描绘可达性条件,我们用投影矩阵
, 是
的伪逆矩阵。因为
,那么
,所以考虑矩阵函数
,有以下方程成立
是
的伪逆矩阵。因为
,那么
,所以考虑矩阵函数
,有以下方程成立
(8)
矩阵
由以下得出
(9)
C是满足
任意的
矩阵。
引理1当
,矩阵
是可达的当且仅当条件(8)成立且满足
[9]。
5. 随机受控金融系统的数值模拟
(10)
,
是控制部分。由图3可以看出在
和
之间,平衡点 的随机灵敏度非常大。
的随机灵敏度非常大。
接下来考虑带有控制的系统(10),控制的目的是稳定平衡点
,使得在区间
内,所有的随机状态都集中在平衡点小邻域内。我们的方法是为
合成随机灵敏度矩阵
。
反馈控制器的系数
取决于满足(9)的随机灵敏度矩阵 ,对于系统(10)
,对于系统(10)
我们有

Figure 3. Stochastic sensitivity of equilibrium point
of uncontrolled financial system
图3. 非受控金融系统的平衡点
的随机灵敏度
由可达性条件可以得到
这里,五个元素有三个方程,由于参数可以自由选择,所以我们可以固定
,所以就有显示公式
再由W的正定性,有
,所以我们选取
所以我们想要得到的随机灵敏度矩阵就可以表示为
可以发现受控系统的随机灵敏度矩阵远远小于非受控系统的随机灵敏度矩阵,由图4可以看出受控系统的
在整个
上保持在6.5左右。

Figure 4. Stochastic sensitivity of equilibrium point
of controlled financial system
图4. 受控金融系统的平衡点
的随机灵敏度
接下来验证受控系统的随机灵敏度可以抑制随机振荡,由引理和(10)可以得到控制器的系数
当
时,
,
当
时,
,
当
时,
。
将每个
带入到相对应
值的系统中,系统稳定在
,由图5可以看到,加入控制器后随机轨迹的
坐标稳定在一个常数。
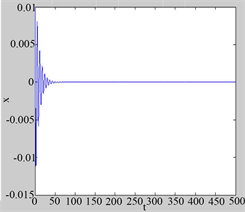


Figure 5. Stability of random oscillation in x-coordinate of random trajectory
图5. 随机轨迹x坐标的随机振荡的稳定
6. 结论
1) 不加控制项的随机系统的随机轨迹会发散在平衡位置周围,加入控制项后,可以将随机轨迹稳定在平衡位置的小邻域内。
2) 加入控制项后可以实现随机振荡的稳定,并且其稳定性的实现是由于受控系统平衡位置的随机灵敏度的降低。
参考文献