具有间接吸引信号产出的高维趋化增长系统解的有界性

Boundedness in the Higher-Dimensional Chemotaxis-Growth System with Indirect Attractant Production

摘要: 本文考虑一个具有间接信号产出的山松甲壳虫趋化增长系统： ，其中是一个光滑有界区域，τ>0。利用能量方法和Moser迭代证明了在任意充分光滑的初值边界条件下，当µ足够大，该模型有唯一的全局有界经典解。

Abstract: This paper deals with the following Chemotaxis-growth system of the Mountain Pain Beetle with in-direct attractant production: in a smoothly bounded domain ,   is positive. The energy method and Moser iteration are used to prove that under any sufficiently smooth initial boundary conditions, when µ is large enough, the model has a unique global-in-time classical solution.

1. 引言

本文考虑了具有间接信号产生的趋化增长模型：

$\{\begin{array}{cc}{u}_t=\Delta u-\nabla \cdot \left(u\nabla v\right)\text{+}\mu \left(u-u^2\right),& x\in \Omega ,t>0,\\ v_t=\Delta v+w-v,& x\in \Omega ,t>0,\\ \tau w_t+w=u,& x\in \Omega ,t>0,\\ \frac{\partial u}{\partial n}=\frac{\partial v}{\partial n}=\frac{\partial w}{\partial n}=0,& x\in \partial \Omega ,t>0,\\ u\left(x,0\right)=u_0\left(x\right),v\left(x,0\right)=v_0\left(x\right),w\left(x,0\right)=w_0\left(x\right),& x\in \Omega ,\end{array}$ (1.1)

其中 $\Omega \subset {ℝ}^n\left(n\ge 3\right)$ 是一个光滑有界区域， $\tau >0$ 。 $u=u\left(x,t\right)$ 表示飞行甲壳虫的密度， $v=v\left(x,t\right)$ 表示做窝甲壳虫释放的化学信号浓度， $w=w\left(x,t\right)$ 表示做窝甲壳虫的密度。山松甲壳虫的模型最早由Strohm，Tyson和Powell [1] 提出，该模型是为了研究山松甲壳虫的趋化行为。趋化行为是指由化学信号浓度梯度引起细胞的偏向运动，细胞偏向于朝化学信号浓度增加的地方移动 [2] [3] [4]。著名的趋化模型是由Keller-Segel于1970年提出 [5] ，具体表示为：

$\{\begin{array}{cc}{u}_t=\Delta u-\nabla \cdot \left(u\nabla v\right),& x\in \Omega ,t>0,\\ v_t=\Delta v-v+u,& x\in \Omega ,t>0\\ \frac{\partial u}{\partial n}=\frac{\partial v}{\partial n}=0,& x\in \partial \Omega ,t>0,\\ u\left(x,0\right)=u_0\left(x\right),v\left(x,0\right)=v_0\left(x\right),& x\in \Omega ,\end{array}$

其中 $\Omega \subset {ℝ}^n$ 是一个光滑有界区域， $u$ 表示细胞密度； $v$ 表示细胞产生的化学信号浓度。Keller-Segel模型中的化学信号是由细胞直接产出的，不同于Keller-Segel模型的是模型(1.1)飞行的甲壳虫在松树上做窝产卵变为做窝的甲壳虫产出 [6]。

当 $n=3$ ， $\mu >0$ 时，Hu和Tao在文献 [7] 中证明了模型解的全局有界性。本文证明了 $n\ge 3$ ， $\mu >{\delta }_2+C\left(p\right)\left(2{\delta }_1+\epsilon \right)$ 时，模型(1.1)解的全局有界性，其中 ${\delta }_1$ ， ${\delta }_2$ ， $C\left(p\right)$ 满足(3.7)，(3.11)，(3.9)。当 $n\ge 2$ 时，Li和Tao [8] 研究了logistic源为 $u-u^{\alpha }$ 时的情况，系数满足 $\alpha >n/2$ 时模型解的全局有界性，维数 $n\ge 4$ 时，显然 $\alpha >2$ ，而本文 $\alpha =2$ 优于其结果。在Hu和Tao研究的基础上，Qiu，Mu和Wang [9] 将飞行甲壳虫的随机扩散项 $\Delta u$ 用非线性函数 $D\left(u\right)$ 来描述，考虑扩散系数 $D\left(u\right)$ 对模型的影响，当 $n\ge 3$ 时，假设扩散系数 $D\left(u\right)>D_0{u}^{\theta }$ 得到 $\theta >1-4/n$ 时模型解的全局有界性。而当 $n\ge 4$ 时，本文 $\theta =0$ 优于其结果。当 $n\ge 1$ 时，Zheng在文献 [10] 中假设扩散系数 $D\left(u\right)\ge C_D{\left(u+1\right)}^{m-1}$ 得到 $m>\{\begin{array}{cc}1-\frac{\mu }{\chi \left[1+{\lambda }_0{\Vert v_0\Vert }_{L^{\infty }\left(\Omega \right)}{2}^3\right]}& n\le 2,\\ 1& n\ge 3,\end{array}$ 时模型解的全局有界性。但是本文 $n\ge 3$ 时是文献 [10] 的一个临界情况。

本文在证明解的全局有界性时，先建立 ${\displaystyle {\int }_{\Omega }{u}^2\left(\cdot ,t\right)}\text{d}x$ 和 ${\Vert v\left(\cdot ,t\right)\Vert }_{W^{1,q}\left(\Omega \right)}\le C$ 一致先验估计，再建立飞行甲壳虫 $u$ 的 $L^p\left(\Omega \right)$ 一致估计，再由Moser迭代推得 $u$ 的 $L^{\infty }\left(\Omega \right)$ 一致有界性，进而根据抛物型方程Neumann边值问题的正则性理论推得 $v$ 和 $w$ 的一致有界性。具体地说，有以下结果。

定理1： $n\ge 3$ ，假设 $u_0\in C^0\left(\bar{\Omega }\right)$ ， $v_0\in C^1\left(\bar{\Omega }\right)$ ， $w_0\in C^1\left(\bar{\Omega }\right)$ ， $u_0\ge 0$ ， $v_0\ge 0$ ， $w_0\ge 0$ 和 $u_0\cancel{\equiv }0$ 。存在唯一的非负函数 $\left(u,v,w\right)$ ：

$\begin{array}{l}u\in C^0\left(\bar{\Omega }\times \left[0,T{}_{\max }\right)\right)\cap C^{2,1}\left(\bar{\Omega }\times \left(0,T_{\max }\right)\right),\\ v\in C^0\left(\bar{\Omega }\times \left[0,T{}_{\max }\right)\right)\cap C^{2,1}\left(\bar{\Omega }\times \left(0,T_{\max }\right)\right),\\ w\in C^{0,1}\left(\bar{\Omega }\times \left[0,T{}_{\max }\right)\right),\end{array}$

在 $\Omega \times \left(0,\infty \right)$ 是模型(1.1)的经典解。特别的，存在一个常数 $C>0$ ，使得

$u\left(x,t\right)\le C$ ， $v\left(x,t\right)\le C$ 和 $w\left(x,t\right)\le C,x\in \Omega$ ， $t>0$ 。

2. 先验估计

为了证明定理1结果，首先介绍两个基本引理用于主要结论的证明。

引理1：假设 $n\ge 3$ ， $p>\max \left\{1,\frac{n-2}{2}\right\}$ ，则存在正常数 $k_0$ 使得

${\Vert \nabla v\Vert }_{L^{2p+2}\left(\Omega \right)}^{2p+2}\le k_0\left({\Vert {\left|\nabla v\right|}^{p-1}{D}^{2}v\Vert }_{L^2\left(\Omega \right)}^2+1\right)$ 。

证明：在文献 [10] 中的引理2.7中有详细的证明过程。

要证明模型(1.1)的解全局有界，关键要建立 ${\displaystyle {\int }_{\Omega }{u}^2\left(\cdot ,t\right)}\text{d}x$ 和 ${\Vert v\left(\cdot ,t\right)\Vert }_{W^{1,q}\left(\Omega \right)}\le C$ 的一致先验估计。

引理2：假设 $n\ge 3$ ，对于任意 $t\in \left(0,T_{\max }\right)$ ，存在正常数 $C>0$ ，使得模型(1.1)的解 $\left(u,v,w\right)$ 满足

${\displaystyle {\int }_{\Omega }u\left(\cdot ,t\right)\text{d}x\le C}$ ， ${\Vert v\left(\cdot ,t\right)\Vert }_{W^{1,q}\left(\Omega \right)}\le C$ 和 ${\displaystyle {\int }_{\Omega }{u}^2\left(\cdot ,t\right)\text{d}x\le C}$ 。

证明：Hu和Tao在文献 [7] 中的引理2.2和引理4.4中证明了 ${\displaystyle {\int }_{\Omega }u\left(\cdot ,t\right)}\text{d}x$ 和 ${\displaystyle {\int }_{\Omega }{u}^2\left(\cdot ,t\right)}\text{d}x$ 的有界性。由 ${\displaystyle {\int }_{\Omega }{u}^2\left(\cdot ,t\right)}\text{d}x$ 的有界性可以得到 ${\displaystyle {\int }_{\Omega }{w}^2\left(\cdot ,t\right)}\text{d}x\le C$ ，从而利用Horstmann和Winkler在文献 [11] 中的引理4.1得到 ${\Vert v\left(\cdot ,t\right)\Vert }_{W^{1,q}\left(\Omega \right)}\le C$ ，其中 $q<\frac{2n}{n-2}$ 。

3. 主要结论的证明

根据引理2中的先验估计，我们下面利用引理1和Young不等式来估计 $u$ 的 $L^p\left(\Omega \right)$ ， $\nabla v$ 的 $L^{2p}\left(\Omega \right)$ 和 $w$ 的 $L^{p+1}\left(\Omega \right)$ 的有界性。

引理3：设 $p>\max \left\{1,\frac{n-2}{2}\right\}$ ，若 $\mu$ 足够大，则对于任意的 $t\in \left(0,T_{\max }\right)$ ，存在正常数 $C:=C\left(p,\left|\Omega \right|,\mu \right)$ 使得趋化模型(1.1)的解 $\left(u,v,w\right)$ 满足

${\Vert u\Vert }_{L^p\left(\Omega \right)}^p\le C$ ， ${\Vert \nabla v\Vert }_{L^{2p}\left(\Omega \right)}^{2p}\le C$ 和 ${\Vert w\Vert }_{L^{p\text{+}1}\left(\Omega \right)}^{p\text{+}1}\le C$ 。

证明：第一步：对于任意的 $t\in \left(0,T_{\max }\right)$ ，利用 $\nabla v\cdot \nabla \left(\Delta v\right)=\frac{1}{2}\Delta {\left|\nabla v\right|}^2-{\left|D^{2}v\right|}^2$ 和趋化模型(1.1)的第二个方程，经过简单的直接计算可得

$$ (3.1)

对于等式(3.1)中的I项，取 $r\in \left(0,\frac{1}{2}\right)$ ，则由 $W^{r+\frac{1}{2},2}\left(\Omega \right)$ 紧嵌入在 $L^2\left(\partial \Omega \right)$ 可得

$\frac{1}{2}{\displaystyle {\int }_{\partial \Omega }{\left|\nabla v\right|}^{2p-2}\frac{\partial {\left|\nabla v\right|}^2}{\partial n}}\text{d}x\le \frac{1}{2}{C}_{\Omega }{\Vert {\left|\nabla v\right|}^p\Vert }_{L^2\left(\partial \Omega \right)}^2\le C_1{\Vert {\left|\nabla v\right|}^p\Vert }_{W^{r+\frac{1}{2},2}\left(\Omega \right)}^2$ ， (3.2)

进一步，通过Gagliardo-Nirenberg不等式和 ${\left|\nabla v\right|}^2$ 的有界性，则存在 $a\in \left(0,1\right)$ 使得

${\Vert {\left|\nabla v\right|}^p\Vert }_{W^{r+\frac{1}{2},2}\left(\Omega \right)}^2\le C_2{\Vert {\left|\nabla v\right|}^p\Vert }_{L^2\left(\Omega \right)}^a\text{+}{C}_3\le \frac{p-1}{C_1{p}^2}{\displaystyle {\int }_{\Omega }{\left|\nabla {\left|\nabla v\right|}^p\right|}^2}\text{d}x\text{+}{C}_4$ ，

联合不等式(3.2)可得

。 (3.3)

此外，对于等式(3.1)中的II项，利用Young不等式可知

$\begin{array}{c}-{\displaystyle {\int }_{\Omega }w\nabla v\cdot \nabla \left({\left|\nabla v\right|}^{2p-2}\right)}\text{d}x=-\left(p-1\right){\displaystyle {\int }_{\Omega }w{\left|\nabla v\right|}^{2\left(p-2\right)}}\nabla v\cdot \nabla {\left|\nabla v\right|}^2\text{d}x\\ \le \frac{p-1}{4}{\displaystyle {\int }_{\Omega }{\left|\nabla v\right|}^{2p-4}}{\left|\nabla {\left|\nabla v\right|}^2\right|}^{2}dx+\left(p-1\right){\displaystyle {\int }_{\Omega }{w}^2{\left|\nabla v\right|}^{2p-2}}\text{d}x\\ \le \frac{p-1}{p^2}{\displaystyle {\int }_{\Omega }{\left|\nabla {\left|\nabla v\right|}^p\right|}^2}\text{d}x\text{+}\left(p-1\right){\displaystyle {\int }_{\Omega }{w}^2{\left|\nabla v\right|}^{2p-2}\text{d}x}.\end{array}$ (3.4)

另一方面，对于等式(3.1)中的III项，利用估计 $\left|\Delta v\right|\le \sqrt{n}\left|D^{2}v\right|$ 和Young不等式可得

$-{\displaystyle {\int }_{\Omega }w{\left|\nabla v\right|}^{2p-2}}\Delta v\text{d}x\le \sqrt{n}{\displaystyle {\int }_{\Omega }w{\left|\nabla v\right|}^{2p-2}}\left|D^{2}v\right|\text{d}x\le \frac{1}{4}{\displaystyle {\int }_{\Omega }{\left|\nabla v\right|}^{2p-2}{\left|D^{2}v\right|}^2}\text{d}x\text{+}n{\displaystyle {\int }_{\Omega }{w}^2{\left|\nabla v\right|}^{2p-2}}\text{d}x$ 。 (3.5)

最后，利用Young不等式和引理1可得

$\begin{array}{c}{\displaystyle {\int }_{\Omega }{w}^2{\left|\nabla v\right|}^{2p-2}}\text{d}x\le \frac{1}{4\left(n+p-1\right)k_0}{\displaystyle {\int }_{\Omega }{\left|\nabla v\right|}^{2p+2}}\text{d}x+\frac{2}{p+1}{\left(\frac{4\left(n+p-1\right)\left(p-1\right)k_0}{p+1}\right)}^{\frac{p-1}{2}}{\displaystyle {\int }_{\Omega }{w}^{p+1}}\text{d}x\\ \le \frac{1}{4\left(n+p-1\right)}{\displaystyle {\int }_{\Omega }{\left|\nabla v\right|}^{2p-2}{\left|D^{2}v\right|}^2}\text{d}x+{\delta }_1{\displaystyle {\int }_{\Omega }{w}^{p+1}}\text{d}x+C，\end{array}$ (3.6)

联合不等式(3.1)和(3.3)~(3.6)可得

$\frac{1}{2p}\frac{\text{d}}{\text{d}t}{\Vert \nabla v\Vert }_{L^{2p}\left(\Omega \right)}^{2p}+{\displaystyle {\int }_{\Omega }{\left|\nabla v\right|}^{2p}}\text{d}x+\frac{1}{2}{\displaystyle {\int }_{\Omega }{\left|\nabla v\right|}^{2p-2}{\left|D^{2}v\right|}^2}\text{d}x\le {\delta }_1{\displaystyle {\int }_{\Omega }{w}^{p+1}}\text{d}x+C,$ (3.7)

其中。

第二步：为了处理不等式(3.7)右端的项 ${\delta }_1{\displaystyle {\int }_{\Omega }{w}^{p+1}}\text{d}x$ ，对趋化模型(1.1)的第三个方程乘以 $w^p$ 并在 $\Omega$ 上进行积分并利用Young不等式可得

$\frac{\tau }{p+1}\frac{\text{d}}{\text{d}t}{\Vert w\Vert }_{L^{p+1}\left(\Omega \right)}^{p+1}+{\displaystyle {\int }_{\Omega }{w}^{p+1}}\text{d}x={\displaystyle {\int }_{\Omega }u{w}^p}\text{d}x\le \frac{1}{2}{\displaystyle {\int }_{\Omega }{w}^{p+1}}\text{d}x+C\left(p\right){\displaystyle {\int }_{\Omega }{u}^{p+1}}\text{d}x$ ， (3.8)

即

$\frac{\tau }{p+1}\frac{\text{d}}{\text{d}t}{\Vert w\Vert }_{L^{p+1}\left(\Omega \right)}^{p+1}+\frac{1}{2}{\displaystyle {\int }_{\Omega }{w}^{p+1}}\text{d}x\le C\left(p\right){\displaystyle {\int }_{\Omega }{u}^{p+1}}\text{d}x$ 。 (3.9)

其中 $C\left(p\right)=\frac{1}{p+1}{\left(\frac{p+1}{2p}\right)}^{-p}$ 。

第三步：为了处理不等式(3.9)右端的项 ${\displaystyle {\int }_{\Omega }{u}^{p+1}}\text{d}x$ ，对趋化模型(1.1)的第一个方程乘 $u^{p-1}$ 并在 $\Omega$ 上进行积分可得

$\frac{1}{p}\frac{\text{d}}{\text{d}t}{\Vert u\Vert }_{L^p\left(\Omega \right)}^p+\left(p-1\right){\displaystyle {\int }_{\Omega }{u}^{p-2}{\left|\nabla u\right|}^2}\text{d}x=-{\displaystyle {\int }_{\Omega }\nabla \cdot \left(u\nabla v\right)u^{p-1}}\text{d}x+\mu {\displaystyle {\int }_{\Omega }{u}^p}\text{d}x-\mu {\displaystyle {\int }_{\Omega }{u}^{p+1}}\text{d}x.$ (3.10)

对于等式(3.10)右端的第一项，应用Young不等式和引理1可得

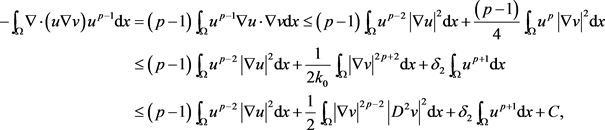
其中 ${\delta }_2\text{=}\frac{p{k}_0^p{\left(p-1\right)}^{p+1}}{2^{p+2}{\left(p+1\right)}^{p+1}}$ 。进而可得

$\frac{1}{p}\frac{\text{d}}{\text{d}t}{\Vert u\Vert }_{L^p\left(\Omega \right)}^p\text{+}\frac{1}{p}{\Vert u\Vert }_{L^p\left(\Omega \right)}^p\le \frac{1}{2}{\displaystyle {\int }_{\Omega }{\left|\nabla v\right|}^{2p-2}{\left|D^{2}v\right|}^2}\text{d}x\text{+}\left(\mu +\frac{1}{p}\right){\displaystyle {\int }_{\Omega }{u}^p}\text{d}x-\left(\mu -{\delta }_2\right){\displaystyle {\int }_{\Omega }{u}^{p+1}}\text{d}x+C.$ (3.11)

现在，由(3.7) + (3.9) $\times \left(2{\delta }_1+\epsilon \right)$ + (3.11)可得

$\begin{array}{l}\frac{\text{d}}{\text{d}t}\left[\frac{1}{2p}{\Vert \nabla v\Vert }_{L^{2p}\left(\Omega \right)}^{2p}+\frac{\tau \left(2{\delta }_1+\epsilon \right)}{p+1}{\Vert w\Vert }_{L^{p+1}\left(\Omega \right)}^{p+1}+\frac{1}{p}{\Vert u\Vert }_{L^p\left(\Omega \right)}^p\right]+{\displaystyle {\int }_{\Omega }{\left|\nabla v\right|}^{2p}}\text{d}x+\frac{\epsilon }{2}{\displaystyle {\int }_{\Omega }{w}^{p+1}}\text{d}x+\frac{1}{p}{\Vert u\Vert }_{L^p\left(\Omega \right)}^p\\ \le \left(\mu +\frac{1}{p}\right){\displaystyle {\int }_{\Omega }{u}^p}\text{d}x-\left[\mu -{\delta }_2-C\left(p\right)\left(2{\delta }_1+\epsilon \right)\right]{\displaystyle {\int }_{\Omega }{u}^{p+1}}\text{d}x+C,\end{array}$

其中 $\epsilon$ 是任意给定的小常数。若 $\mu -{\delta }_2-C\left(p\right)\left(2{\delta }_1+\epsilon \right)>0$ ，则利用Young不等式和Gronwall不等式可得

${\Vert \nabla v\Vert }_{L^{2p}\left(\Omega \right)}^{2p}\le C$ ， ${\Vert w\Vert }_{L^{p+1}\left(\Omega \right)}^{p+1}\le C$ 和 ${\Vert u\Vert }_{L^p\left(\Omega \right)}^p\le C$ 。

事实上，若引理3中的 $p\ge n-1$ ，则由抛物型方程Neumann边值问题的正则性理论 [12] 可得如下结论。

引理4：设 $\left(u,v,w\right)$ 是趋化模型(1.1)的解，若 $\mu$ 足够大，那么对于任意的 $t\in \left(0,T_{\max }\right)$ ，都存在一个常数 $C>0$ 使得

${\Vert \nabla v\left(\cdot ,t\right)\Vert }_{L^{\infty }\left(\Omega \right)}\le C$ 。

在引理3和引理4的基础上，我们有如下的结论。

引理5：若 $u_0\in C^0\left(\bar{\Omega }\right)$ ， $v_0\in C^1\left(\bar{\Omega }\right)$ 和 $w_0\in L_{\infty }\left(\bar{\Omega }\right)$ 是非负的，若 $\mu$ 足够大，那么对于任意的存在 $t\in \left(0,\infty \right]$ ，存在常数 $C>0$ ，使得

${\Vert u\left(\cdot ,t\right)\Vert }_{L^{\infty }\left(\Omega \right)}\le C$ 和 ${\Vert w\left(\cdot ,t\right)\Vert }_{L^{\infty }\left(\Omega \right)}\le C$ 。

证明：对于任意的 $p>1$ ，对趋化模型(1.1)的第一个方程两边同时乘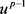并在 $\Omega$ 进行积分，然后借助于Young不等式和引理4，容易得到

$\begin{array}{c}\frac{1}{p}\frac{\text{d}}{\text{d}t}{\Vert u\Vert }_{L^p\left(\Omega \right)}^p+\left(p-1\right){\displaystyle {\int }_{\Omega }{u}^{p-2}{\left|\nabla u\right|}^2}\text{d}x\le \left(p-1\right){\displaystyle {\int }_{\Omega }{u}^{p-1}\left|\nabla u\right|}\left|\nabla v\right|\text{d}x+\mu {\displaystyle {\int }_{\Omega }{u}^{p-1}\left(u-u^2\right)}\text{d}x\\ \le C{\displaystyle {\int }_{\Omega }{u}^{p-1}\left|\nabla u\right|}\text{d}x+\mu {\displaystyle {\int }_{\Omega }{u}^{p-1}\left(u-u^2\right)}\text{d}x\le \frac{p-1}{4}{\displaystyle {\int }_{\Omega }{u}^{p-2}{\left|\nabla u\right|}^2}\text{d}x\\ +C{\displaystyle {\int }_{\Omega }{u}^p}\text{d}x+\mu {\displaystyle {\int }_{\Omega }{u}^{p-1}\left(u-u^2\right)}\text{d}x\\ \le \frac{p-1}{4}{\displaystyle {\int }_{\Omega }{u}^{p-2}{\left|\nabla u\right|}^2}\text{d}x+C{\displaystyle {\int }_{\Omega }{u}^p}\text{d}x-\mu {\displaystyle {\int }_{\Omega }{u}^{p+1}}\text{d}x.\end{array}$

这样利用Young不等式可得

$\frac{1}{p}\frac{\text{d}}{\text{d}t}{\Vert u\Vert }_{L^p\left(\Omega \right)}^p+\frac{1}{p}{\displaystyle {\int }_{\Omega }{u}^p}\text{d}x+\frac{p-1}{p^2}{\displaystyle {\int }_{\Omega }{\left|\nabla u^{\frac{p}{2}}\right|}^2}\text{d}x\le C$ ，

进一步利用Gronwall不等式可得证

${\Vert u\left(\cdot ,t\right)\Vert }_{L^p\left(\Omega \right)}\le C$ 。

那么在引理4和引理5的基础上，运用标准的Alikakos-Moser迭代 [13] 可得证

${\Vert u\left(\cdot ,t\right)\Vert }_{L^{\infty }\left(\Omega \right)}\le C$ 。

最后利用趋化模型(1.1)第三个一阶线性常微分方程的解，显然可得

${\Vert w\left(\cdot ,t\right)\Vert }_{L^{\infty }\left(\Omega \right)}\le C$ 。

从而定理1得证。

注1：本文在 $\mu$ 足够大的条件下证明了方程解的全局有界性，事实上，若Logistic源项变为 $\mu u-\mu u^{\alpha }$ ，从引理3的证明可以看出，当 $\alpha >2$ 时，对任意 $\mu >0$ 趋化模型的解全局存在，证明过程只需要简单修改即可。

基金项目

自治区青年科技创新人才培养项目“偏微分方程理论及其在图像处理中的应用”(2017Q081)。

NOTES

^*通讯作者。