1. 引言
最优控制问题在各个领域的研究中都有着越来越广泛的应用,它一般是通过控制某些变量,寻找到最优策略以达到某项指标。近几年来,保险精算解特别关注最优分红、注资以及最优投资策略问题的研究,比如带有交易费用的分红等。但生活中会有各种法规的禁止和规定、实际金融投资市场中限制因素有可能不允许卖空等,这些都要求模型的建立更加有实际指导意义,同时也使得建立的模型更加难解。
近几年来,保险公司的最优投资和再保险成为保险行业最吸引眼球的问题。自从Borch K.开创了再保险研究的先河,Browne [1] 用一个带漂移的几何布朗运动对保险公司的盈余进行模拟,研究了保险公司在进行风险资产价格符合几何布朗运动的投资时的最优投资策略;梁志彬 [2] 研究了当保险公司的盈余服从跳–扩散过程时的最优投资和再保险策略问题,在终端财富期望指数效用最大化的准则下求出了最优投资再保险和值函数的解析表达式。杨鹏,林祥 [3] 在比例再保险带交易费用的情况下研究了同样的问题;林祥,杨鹏 [4] 则研究了比例再保险和投资对分红的影响,在分红方式是常数边界分红的条件下得出了最优投资再保险策略。杨鹏,林祥 [5] 研究了跳–扩散风险模型和扩散风险模型下相似的问题,但是他们的创新点在于风险资产的价格服从跳–扩散模型,并且考虑了随机利率和随机波动率,而且假设保费收入符合复合泊松过程。
分红的问题自De Finetti [6] 对离散时间序列下的分红模型进行初次研究提出最优分红的问题之后,关于分红策略的研究就一直是精算界的重头戏。专门针对如何分红的研究已经达到非常成熟的阶段,但是对于一个企业来说在保证盈利分红的情况下,如何制定可靠的风险控制策略以及有效地使用货币的时间价值在市场上进行投资获利也是非常重要的,目前做此类文章的并不多见,但这类研究却是企业在经营中必不可少的理论依据,鉴于这种情况下,我们就该领域的研究在前人的基础上进一步探讨研究。
在早期的文章中有很多文献对原始的复合泊松风险模型以及扩散风险模型的最优分红策略问题进行了研究,比如Buhlmann H. [7] ,Asmussen S.,Taksar M. [8] 。程恭品 [9] 对带交易费用和破产终端值影响下的最优分红和风险控制策略进行了详细的研究,从比例再保险到超额损失再保险,以及在分红限速的情况下的最优分红和注资问题均给出了充分的解答;林祥,杨鹏 [4] 在扩散模型下研究了比例再保险和投资对分红的影响,考虑在常数边界分红策略下的期望贴现红利最大;Shreve [10] 已经证明了在以期望累积分红现值最大化为准则的情况下,最优分红策略为Barrier策略;杨鹏 [11] 在跳–扩散风险模型下,找到了使得分红最大的投资策略,也给出了在分布已知的情况下具体的JHB方程的求解方法。到目前为止还很少有文献研究扩散风险模型下常数边界分红策略对最优比例再保险和投资策略的影响。林祥,杨鹏(2010) [4] 研究分红策略对再保险和投资策略的影响时,虽有考虑投资,但是却忽略了在实际情况中企业会有无风险投资,本文就投资这方面在林祥的基础上进一步扩展,研究在引入无风险投资的情况下,分红策略对再保险和投资策略的影响。
2. 模型
考虑保险公司原始风险模型为如下扩散风险模型:
其中
为初始盈余,
为保险公司的保费收入率(本章中的保费收入率是考虑理赔之后的一个综合收入率),
表示由于保费收入或者理赔引起盈余的不定项波动。考虑比例再保险,假设保险公司的再保险自留比例为
,
,则考虑再保险之后保险公司的盈余过程如下表示:
保险公司可以投资价格
如下的无风险资产:
其中
表示无风险利率。同时允许保险公司在风险资产市场进行价格
符合几何布朗运动的风险投资:
其中
表示风险资产的瞬时期望收益率,
表示风险资产的标准差,
为与
相互独立的标准布朗运动。
我们假设风险资产投资的比例为
,
,记再保险投资策略为
,这里将所有可行策略的集合用
表示,我们称策略
为可行的,如果满足:
1)
关于
可测;
2)
;
3)
。
则经过策略
作用之后的盈余过程
如下描述:
我们记
为到时间
为止的累积分红额,在时刻
经过分红之后的盈余记为
,则有:
定义破产时间为:
在分红时采用边界分红策略,分红边界值为
,即当盈余超过边界
时,将超出部分全部作为红利进行分红,盈余不足
时不进行分红。这里考虑的指标为破产时的期望累积贴现分红最大,我们记
为贴现率,则值函数可以表示为:
满足上式的
称为最优策略。
3. 最优策略
在求解上述问题之前我们先给出相应的HJB方程和验证定理,根据Schmidli [12] 容易得到下面的定理
定理3.1:(HJB方程)若
为定义在
上的二次连续可微函数,则有下面的HJB方程
(1)
(2)
并且满足以下的边界条件
(3)
通过Flemming和Soner [13] 中介绍的标准求解方法,我们可以得到以下验证定理3.2。
定理3.2:(验证定理)若
为定义在
上的二次连续可微的凹函数,并且是满足边界条件(3) HJB方程(1)和(2)的解,则值函数
与
是一致的,也就是说
。我们称
为最优策略,如果它满足以下两个条件:
接下来我们求解HJB方程(1),令
通过
分别对
求导等于
可以得到最优再保险策略和投资策略
(4)
(5)
将(4)和(5)带入到HJB方程(1)中化简得到:
上式两边同乘
,并且令
则有:
(6)
我们令
则有
,
将上式带入到方程(6)得到
通过求解上述方程得
(7)
其中
为常数。通过常系数齐次线性微分方程及欧拉变换可以求解上述方程(7),解得最优再保险策略为:
最优风险投资比例为:
我们令
,
则值函数为:
注1:因为再保险自留比例要求
,所以最优再保险比例表达式和值函数总要求
。
注2:没有进行再保险和投资情况下的值函数以及含有比例再保险和风险投资情况下的值函数的相关结果在林祥,杨鹏 [4] 都已经给出,我们不再重复计算,这里直接对其结果进行比较。
4. 数值分析
为了与林祥,杨鹏(2010) [4] 结果比较更加方便,更直观地看出无风险投资对最优策略的影响,这里我们取与其相同的参数值。
4.1. 无风险利率r0对红利的影响
我们取
,常数边界分红为
,则值函数与盈余
之间的关系如图1所示。
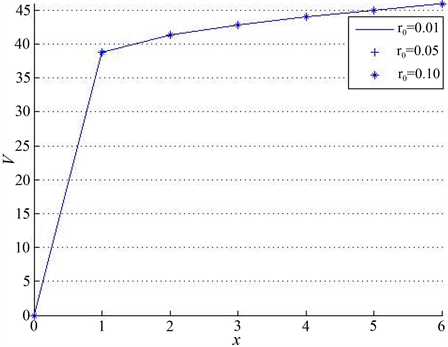
Figure 1. The relationship between the value function
and
and
图1. 值函数
与
和
之间的关系
通过图1与林祥,杨鹏 [4] 的图1对比可以得知:加入无风险投资之后期望分红会减小,但是无风险利率
的变化并不会影响分红策略以及值函数的走势。
4.2. 参数r0,μ对最优投资策略p*的影响
我们取
则可以得到保险公司的风险暴露水平
与参数
的关系:
通过图2可知:最优风险投资比例是风险资产瞬时期望收益率
的增函数,这与实际情况是相符的,也与林祥,杨鹏 [4] 的结果一致。而随着无风险利率
的增加,最优风险投资的比例在减小,也就意味着当无风险投资回报增高时投资人更加倾向于低风险高收益的投资,会相应地减少在风险投资的比重,这与实际情况时吻合的。
4.3. 参数r0,μ对最优再保险策略q*的影响
我们取
则可以得到图3。从图3可以得知比例再保险最优自留比例
是关于
的增函数,当风险资产收益增加时,保险公司的抗风险能力增强,最优自留风险比例
自然会增加。从图中可以看出,当无风险利率
变化时,三条线是重合的,也就是说引入无风险投资并不会应影响再保险策略。
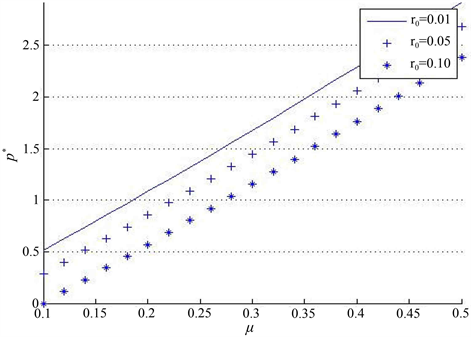
Figure 2. The relationship between optimal investment strategy
and
图2. 最优投资策略
与
的关系

Figure 3. The relationship between optimal reinsurance strategy
and
图3. 最优再保险策略
与
的关系
5. 结论
本文在扩散风险模型下,通过随机控制方法在常数边界分红策略下找到使得期望累积贴现分红最大的组合策略,是对林祥,杨鹏(2010) [4] 的一个扩展,引入无风险资产投资,以及比例风险投资,在林的基础上进行延伸,并得到不一样的值函数,通过数值模拟分析与 [4] 的结果进行对比,发现引入无风险投资使得期望贴现分红值整体减小,无风险利率增加使得最优投资策略减小,但并不会影响最优再保险策略。
6. 展望
本文主要是在前人研究的基础上做的进一步拓展,考虑到实际情况,文章可能存在诸多不足之处,比如在我国金融市场,做空往往是被禁止的,求解结果在实际的应用中会受到市场制度的约束。另外,研究跳–扩散风险模型或者扩散风险模型下研究常数边界分红策略下最优超额损失再保险与在CEV风险资产模型最优策略问题也是一个崭新的方向,有兴趣的学者可以进一步研究。