基于ARIMA模型的北京市雾霾分析、预测与应用

Analysis, Prediction and Application of Beijing Smog Based on ARIMA

摘要: 环境污染一直是我国非常重视的问题，大气污染问题更是重中之重。空气污染物浓度与人们的生活健康息息相关。雾霾是现今秋冬天气中常见的一种天气现象，是由雾和霾组成的，但是两者之间又有很大区别。空气湿度大于90%时称之为雾，霾则小于80%，而雾霾介于两者之间[1]。本文根据北京市的环境污染数据，使用R语言对北京市近十几年的环境污染主要成分的数据进行主成分分析和时间建模，和对环境污染的预测，进而为提高北京市的环境质量，改善居民的生活环境提供依据。

Abstract: Environmental pollution has always been a very important issue in China, especially the air pollution. The concentration of air pollutants is closely related to people’s life and health. Haze is a common weather phenomenon in autumn and winter, it is composed of fog and haze, but there is a big difference between them. When air humidity is greater than 90%, it is called fog, while haze is less than 80%, whereas haze is between the two [1]. Based on the data of environmental pollution in recent ten years in Beijing, this paper uses R language to conduct principal component analysis and to establish the time series model. Utilizing the model, we predict environmental pollution, which provides a basis to improve the environmental quality of Beijing and the living environment of residents.

1. 前言

当前，中国已经成为世界上大气污染最严重的地区之一，尤其是经济发达、人口密集的北京市地区已经成为中国大气污染的重点区域。本文以北京市的环境保护数据为样本，采用2017年发布的北京市统计年鉴中的可吸入颗粒物年日均值(毫克/立方米)、二氧化硫年日均值(毫克/立方米)、二氧化氮年日均值(毫克/立方米)、化学需氧量排放量(万吨)、二氧化硫(SO₂)排放量(万吨)等五种分项污染物年报数据，根据主成分分析法 [2] 提取出主要的几个成分进行分析，并对所得的时间序列进行建模和预测，从数据预测的角度对未来的环境污染的改善给出较为合理的意见。

2. 问题分析

环境污染一直是我们非常重视的问题，本研究利用R软件对北京市2000年到2016年环境污染中的的各成分的监测数据拟合ARIMA模型 [3] ，通过模型对北京市近十几年的环境污染主要成分的数据进行主成分分析和时间建模，和对环境污染的预测，进而控制北京市的环境污染质量。

3. 名词解释

1) ARIMA模型：自回归模型和滑动平均模型的组合，便构成了用于描述平稳随机过程的自回归滑动平均模型ARMA，ARIMA模型的实质就是差分运算与ARMA模型的组合。公式为：

$\{\begin{array}{c}\varphi \left(B\right){\nabla }^d{x}_t=\Theta \left(B\right){\epsilon }_t\\ E\left({\epsilon }_t\right)=0,Var\left({\epsilon }_t\right)={\sigma }_{\epsilon }^2,\\ E\left(x_t{\epsilon }_t\right)=0,\forall s<t\end{array}E\left({\epsilon }_t{\epsilon }_s\right)=0,s\ne t$

4. 时间序列模型的建立

4.1. 主成分分析

4.1.1. 理论知识

主成分分析是由霍特林教授在1933年首先提出的，通过利用了降低维度的思想，在损失较少信息量的前提下，将多个指标转化为有限可数的几个综合指标的方法。一般将转化生成综合指标即为其主成分，每个主成分都是原始变量的线性组合，并且各个主成分之间互不相关，这样使得主成分比原始变量具有某些更为优越的性能，且在研究复杂问题时就可以通过考虑少数的成分而又不损失太多信息进而减少较为繁琐的工作量，抓住主要矛盾，揭示事物内部变量之间的规律性，同时使得问题得到简化，提高分析效率。根据本次主要研究的主题，我们找出了2000~2016年北京市可吸入颗粒物年日均值(毫克/立方米)、二氧化硫年日均值(毫克/立方米)、二氧化氮年日均值(毫克/立方米)、化学需氧量排放量(万吨)、二氧化硫(SO₂)排放量(万吨)。

4.1.2. 主成分模型

1) 数据读取命令：

>data <-read.csv(D:/数据.csv, header = T)

header = T表示将“数据.csv”中的第一行数据设置为列名。

2) 数据进行主成分分析命令：

>wm<-princomp(data, cor = T)

cor = 分析图T的意思是用相关系数进行主成分分析。

3) 绘制主成分分析图命令：

>plot(wm,col=c(6,3,4,2,5))。

4) 观察主成分分析的详细情况命令：

> summary(wm)。

5) 得到各个样本主成分的数据

>wm.p<-predict(wm)。

>wm.p。

4.1.3. 结果

分析：如图1能直观地看出前三个成分是影响北京市环境的主要成分。

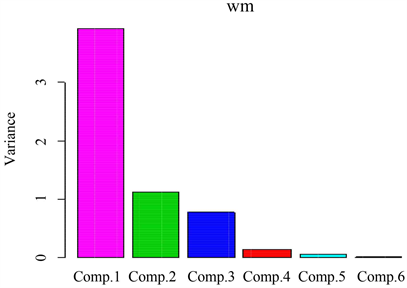
Figure 1. Principal component analysis diagram

图1. 主成分分析图

Importance of components：

Comp. 1 Comp. 2 Comp. 3 Comp. 4 Comp. 5 Comp. 6

Standard deviation：1.98074571.05664390.87433140.36077090.2331760860.10567950

Proportion of Veriance：0.65389230.18608270.12740920.02169260.0090618480.00186136

Cumulative Proportion：0.65389230.83997500.96738420.98907680.9981386401.00000000

数据1

#data1

分析：由于前三个主成分就已经解释了大约96.74%的信息，故只保留了前三个主成分的运行结果如数据1，故影响北京是环境的主要原因依次是可吸入颗粒物排放量、二氧化硫、二氧化氮排放量以及化学需氧量排放量，故后面我们只需分析前三个主成分就行。

Comp. 1 Comp. 2 Comp. 3 Comp. 4 Comp. 5 Comp. 6

[1,] −2.7953416 −1.16328476 −0.12304718 0.48961783 0.081394015 0.062931751

[2,] −2.5273039 −0.99002661 0.05938776 0.22366115 −0.133201839−0.172394829

[3,] −2.6246204 −0.64544256 0.31112562 −0.41546889 −0.054262780−0.194344682

[4,] −1.6855676 −0.11444957 0.40414686 −0.21427260 0.614177705 0.017951433

[5,] −1.7602461−0.04729268 0.54513472 −0.20127834 0.229222346 0.193717402

[6,] −2.1042612 2.57406976 −2.60981821−0.04030502 −0.023750385 −0.002204976

[7,] −1.3946710 0.46523942 0.88082550 −0.12451069 −0.553301903 0.125304156

[8,] −0.7878452 0.53850719 0.83761127 −0.35217839 −0.210918495 0.003035614

[9,] 1.0432882 0.92514125 0.67460190 0.90536454 −0.055716866 −0.060173333

[0,] 0.9956386 0.91366751 0.71035946 0.42563586 0.043621086 0.003578885

[1,] 0.9298532 1.01674034 0.83153373 −0.06776926 0.115433893 0.062296476l

[2,] 1.3898481 −1.31289155 −0.80332081 0.15572978 0.012241809 −0.073888310

[3,] 1.7927033 −1.11349757 −0.79249979 0.28958029 −0.007822765 0.031522806

[4,] 1.7747024 −0.95682552−0.65642048 −0.22527198 0.096963665 0.054875834

[5,] 1.7432168 −0.79753184 −0.43874719 −0.49801314 −0.232194972 −0.004268684

[6,] 2.5979048 −0.53845549 −0.44880075 −0.01881647 −0.085711670 0.128834370

[7,] 3.4127015 1.24633266 0.61792759 −0.33170465 0.163827155 −0.176773912

数据2

#data2

分析：在此条件下，我们所有的结果如数据2，依据主成分的分析所得，故以下分析都是基于主成分分析，所用数据也是通过主成分标准化所求的。

5. 基于ARIMA模型对所得的主成分数据进行预测

本研究利用R软件对北京市2000年到2016年环境污染中的的各成分的监测数据拟合ARIMA模型，并进行预测分析。

5.1. 模型识别

平稳性的判别

1) 理论知识

ARIMA模型建模的基础前提是数据序列应该是平稳非白噪声序列，通过上述对数据主成分的研究，我们基于上述的主成分分析，一般就不在对原始数据进行分析，利用主成分分析得到各主成分数据，但是由于前三个主成分已经解释90%多的信息所以我们只对前三个主成分进行分析研究，即对可吸入颗粒物，二氧化硫，二氧化氮这三组主成分数据进行研究即可。我们将绘制这三组时间序列的时间序列图来判断北京市2000年到2016年这三个序列的平稳性，若不满足平稳性，需要利用“diff”函数进行差分平稳化成平稳序列，此时差分的次数即为ARIMA(p, d, q)模型中的阶数d。

2) 数学模型

1) 时序图绘图命令：

> plot(x,y,type,main,sub,xlab,ylab,xlim,ylim...)

x，y：变量名，可以是数值向量，也可以是一元时间序列名；type：绘图类型。；main = “”：主标题；sub：副标题；xlab = “”：横坐标名称；ylab = “”：纵坐标名称；xlim = c()：横坐标区间；ylim = c()：纵坐标区间。

2) 趋势的消除命令：

>diff(x,lag=,differences=)

x：需要做差分的时间序列名；lag：做差分的步数；differences：做差分的阶数。

3) 结果

分析：如图2可以看出2000年至2016年的北京市环境污染中的可吸入颗粒物所形成的时间序列有一定上升趋势，数据并不是围绕着某个值平稳的上下波动，故可以看出此时间序列是非平稳的。而2000年至2016年的北京市环境污染中的二氧化硫，二氧化氮所形成的时间序列，数据总是围绕着某个值平稳的上下波动，故可以看出这两个时间序列是平稳的。由于可吸入颗粒物所形成的时间序列是非平稳的，我们需要对此数列进行差分。根据图3可以看到经过差分，原来非平稳的可吸入颗粒物所形成的时间序列变成了平稳的时间序列。

5.2. 纯随机性检验

5.2.1. 理论知识

在基础上再在进行数据的纯随机性检验，即根据检验对象提出如下假设条件：

原假设： $H_0:p\left(1\right)=p\left(2\right)=\cdots \cdots =p\left(m\right)=0;\forall m\ge 1$

Figure 2. Sequence chart

图2. 时序图

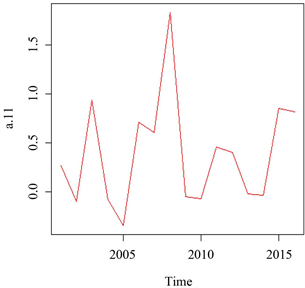
Figure 3. First-order difference diagram of PM10

图3. 可吸入颗粒物一阶差分图

备择假设 $H_1:至少存在某个p\left(k\right)\ne 0\forall m\ge 1,k\le m$

在样本量较小的情形，我们用统计量 $Q_{LB}$ ， $Q_{LB}=n\left(n+2\right){\displaystyle {\sum }_{k=1}^m\frac{p^2}{n-k}}$ 其中，n为序列观察期数，m为指定延迟期数。

当统计量 $Q_{LB}$ 大于 ${\chi }_{1-\alpha }^2\left(m\right)$ 分位数，或它的 $p$ 值小于 $\alpha$ 时，则以 $1-\alpha$ 的置信水平拒绝原假设，并有理由认为备择假设成立，即该序列为非白噪声序列；否则，接受原假设，认为该序列为白噪声序列。

5.2.2. 模型

>Box.test(x,type=,lag=)

x：变量名，可以是数值向量，也可以是一元时间序列名；type：检验统计类型(type = “Box-Pierce”，输出白噪声检验的 $Q_{BP}$ 统计量)。该统计量是默认输出结果。

type = “Ljung-Box”，输出白噪声检验的 $Q_{LB}$ 统计量)；lag：延迟阶数。

5.2.3. 结果

>Box.test (a.11,type = “Ljung-Box”, lag = 9)

Box-Ljung test

Data：a.11

X-squared = 10.749，df = 9，p-value = 0.2933

>Box.test (a.2,type = “Ljung-Box”, lag = 15)

Box-Ljung test

Data：a.2

X-squared = 25.247，df = 15，p-value = 0.04672

>Box.tes (a.3,type = “Ljung-Box”, lag = 15)

Box-Ljung test

Data：a.3

X-squared = 6.6912，df = 15，p-value = 0.9657

数据3

#data3

分析：由所得程序可知除a.2的p值是小于α = 0.05，其余的p值都是大于α = 0.05，故只有a.2在 $1-\alpha$ 的置信区间拒绝原假设，因为原假设是序列是纯随机的，故此序列为非纯随机的，a.1.1、a.3所形成的序列都是纯随机序列，所以只有a.2所形成的时间序列是平稳非白噪声的，因此我们只取a.2为所分析的时间序列。

5.3. 定阶

5.3.1. 理论知识

根据表1利用“acf”和“pacf”函数分析这三组时间序列的自相关图和偏自相关图，进行定阶，判断这三个时间序列ARIMA(p, d, q)模型中的3个参数，其中p为自回归阶数，d为差分阶数，q为滑动平均阶数。

Table 1. Model determination

表1. 模型判定

5.3.2. 结果

分析：如图4中的自相关图可以看出延迟一阶后迅速落回2倍标准差之间，具有短期相关性，故具有平稳的特征，又因为在2倍标准差之间大的多，所以具有拖尾性，p = 1，如图4中的偏自相关图全部都在2倍标准差之间，具有短期相关性，具有平稳的特征，有因为在2倍标准差之间大的多，所以也具有拖尾性，q = 0，综上所述，可以看出这一时间序列服从ARIMA(1, 0, 0)模型。

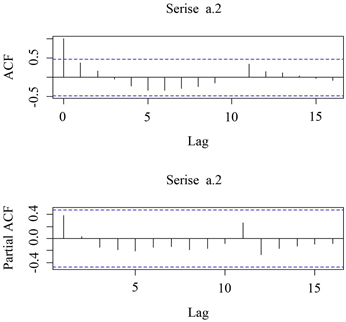
Figure 4. Autocorrelation and partial autocorrelation graphs

图4. 自相关和偏自相关图

5.4. 模型参数估计

5.4.1. 理论知识

所谓的极大似然估计法，指的是建立在极大似然准则基础上的估计方法。极大似然准则认为，样本来自使得该样本出现概率最大的总体。因此，未知参数的极大似然估计就是使得似然函数(即联合密度函数)达到最大的参数值。使用极大似然估计法必须提前知道总体的分布结构。在时间序列分析中，序列总体的具体分布通常未知，为了便于分析和计算，一般假定序列服从多元正态分布。

5.4.2. 数学模型

arima (x,order=,include.mean=,method=)

x：要进行模型拟合的序列名；order：指定模型阶数。Order = c(p, d, q)，其中p为自回归阶数；q为移动平均阶数；d为差分阶数。差分阶数后面章节才会用到，在本次研究中d = 0；include.mean：决定是否包含常数项。如果include. mean = T，那么需要拟合常数项，这是系统默认设置；如果include.mean = F，那么意味着不需要拟合常数项；method：指定参数估计方法，如果method = “CSS-ML”，那么指定参数估计方法是条件最小二乘和极大似然估计混合方法，这是系统默认设置；如果method = “ML”，那么指定参数估计方法是极大似然估计法；如果method = “CSS”，那么指定参数估计方法是条件最小二乘估计法。

5.4.3. 结果

Call:

arima (x = a.2,order = c (1,0,0), method = “ML”)

Coefficients:

arl intercept

0.4176 0.0032

s.e. 0.2293 0.3854

sigma^2 estimated as 0.9285：log likelihood = −23.59，aic = 51.17

数据4

#data4

分析：根据所得结果如数据4我们可以得到模拟口径， $x_t=0.0032x_{t-1}+{\epsilon }_t;{\sigma }_{\epsilon }^2=\mathrm{0.9258.}$

5.5. 模型的检验与优化

5.5.1. 理论知识

如果模型被正确识别，参数估计足够精确，那么残差应该具有白噪声的性质，即残差序列应表现出独立、同分布、零均值和相同标准差的性质。反之，如果残差序列为非白噪声序列，那就意味着残差序列中还残留着相关信息未被提取，说明拟合模型不够有效，需要重新选择其他模型进行拟合。因此，残差的检验指的就是残差序列的白噪声检验。最简单的残差检验就是观察残差序列的时序图。如果残差序列的时序图围绕横轴波动，且波动范围有界，但是波动既无趋势性，也无周期性，表现出较明显的随机性，那么残差序列就可能为白噪声序列。但是较为可靠的检验还是1.2引入的白噪声检验。

原假设 $H_0:p\left(1\right)=p\left(2\right)=\cdots \cdots p\left(m\right)=0,\forall m\ge 1$

备择假设 $H_1:至少存在某个p\left(k\right)\ne 0\forall m\ge 1,k\le m$

当统计量 $Q_{LB}$ 大于 ${\chi }_{1-\alpha }^2\left(m\right)$ 分位数，或它的p值小于 $\alpha$ 时，则以 $1-\alpha$ 的置信水平拒绝原假设，并有理由认为备择假设成立，即该序列为非白噪声序列；否则，接受原假设，认为该序列为白噪声序列。

基于上述信息量的考虑，AIC准则建议评判一个拟合模型的优劣可以从如下两方面考察：

1) 似然函数值的大小。似然函数值越大说明模型拟合的效果越好；

2) 模型中未知参数的个数。模型中未知参数越多，估计的难度就，越大，相应地，估计的精度就越差。

5.5.2. 数学模型

同1.2.2的数学模型一致不再赘述。

5.5.3. 结果

Box-Ljung test

data：a.2. fix $ residual

X-squared = 12.885，df = 15，p-value = 0.6112

数据5

#data5

分析：由所得程序如数据5可知除a.2残差的p值是大于α = 0.05，故a.2残差在 $1-\alpha$ 的置信区间接受原假设，因为原假设是序列是纯随机的，故此序列为纯随机的。

Series：a.2

ARIMA(1, 0, 2) with non-zero mean

Coefficients：

ar1 ma1 ma2 mean

0.2515 0.1538 0.1539 0.0075

s.e.0.7936 0.7996 0.3340 0.3908

sigma^2 estimated as 1.197：log likelihood = −23.49

AIC = 56.97，AICc = 62.43，BIC = 61.14

数据6

#data6

分析：由以上程序如数据6可知对于ARIMA(1, 0, 2)的AIC值是56.97而对于我们所用的ARIMA(1, 0, 0)模型的AIC值是51.17，可以看出ARIMA(1, 0, 0)用的更好一些。

5.6. 预测

5.6.1. 理论知识

时间序列分析的最终目的之一是预测序列未来的变化、发展，所谓预测，就是根据现在与过去的随机序列的样本取值，对未来某个时刻序列值进行估计，目前，许多预测方法都是从线性预测的理论中发展而来的，我们做的残差分析可以看出它是一个平稳序列来讲，最常用的预测方法是线性最小方差预测。

5.6.2. 模型

forecast(object, h=, level=)

object：拟合信息文件名；h：预测期数；level：置信区间的置信水平。不特殊指定的话，一般会自动给出置信水平分别为80%和95%的双层置信区间。

5.6.3. 结果

分析：根据预测如图5可得2017年到2021年的环境污染中的二氧化硫的预测值。如图6可以看出2017年到2021年相对于2016年北京市环境污染有明显的下降趋势环境有所改善。

6. 模型的评价

6.1. 优点

通过主成分分析法利用降维技术 [4] 用少数几个综合变量来代替原始多个变量，但是这些综合变量集中了原始变量的大部分信息，它在应用上侧重于信息量的贡献影响力来进行综合评价，为我们后面的分析减少了大量繁杂的计算步骤，通过时间序列我们可以预测出北京市环境污染的控制有显著的效果。

Figure 5. Prediction of sulfur dioxide

图5. 二氧化硫的预测值

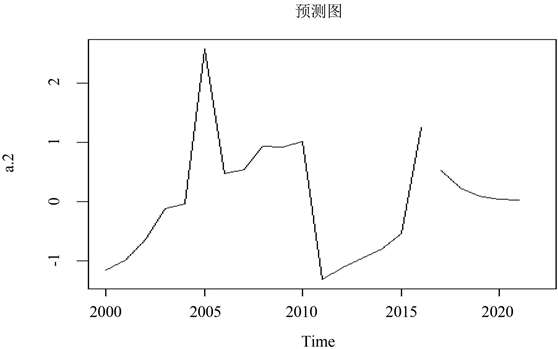
Figure 6. Forecast chart for sulphur dioxide

图6. 二氧化硫的预测图

6.2. 缺点

当主成分的因子负荷的符号有正有负时，综合评价函数意义就不明确，主成分分析方法适用于变量之间存在较强相关性的数据，如果原始数据相关性较弱，则运用主成分分析后不能起到很好的降维作用，根据数据我们建立的模型与实际的情况可能会有所出入，会有一定的模型误差。

7. 总结

在习近平同志的领导下我们对于环境越来越重视，较之前来说我们对污染的控制力度越来越大，但是仍然有所不足，通过我们的模型可以知道二氧化硫在环境污染中占有重要地位，我们应该加强对环境中的二氧化硫的控制，国内的二氧化硫污染源可主要归纳为三个方面：1) 硫酸厂尾气中排放的二氧化硫；2) 有色金属冶炼过程排放的二氧化硫；3) 燃煤烟气中的二氧化硫；因此，我们需要加大力度推广清洁能源，全面推进清洁生产，并且要加大脱硫技术的发展，同时严格管理金属冶炼厂等污染企业。

基金项目

辽宁省自然科学基金面上项目资助(201602188)；校级大创项目(XA201812026276)。

附录

> data <-read.csv(D:/数据.csv, header = T)

> data

>wm<-princomp(data, cor = T)

>wm

>plot(wm,col=c(6,3,4,2,5))

>summary(wm, loadings = T)

>wm.p<-predict(wm)

>wm.p

>wm.p<-data.frame(wm.p)

>a<-wm.p$Comp.1

>b<-wm.p$Comp.2

>c<-wm.p$Comp.3

>a.1<-ts(a,start=2000)

>a.2<-ts(b,start=2000)

>a.3<-ts(c,start=2000)

>par(mfrow=c(3,1))

>plot(a.1,col=2)

>plot(a.2,col=4)

>plot(a.3,col=6)

>a.11<-diff(a.1)

>plot(a.11,col=2)

>Box.test(a.11,type=Ljung-Box,lag=9)

>Box.test(a.2,type=Ljung-Box,lag=15)

>Box.test(a.3,type=Ljung-Box,lag=15)

>par(mfrow=c(2,1))

>acf(a.2,lag=15)

>pacf(a.2,lag=15)

> a.2.fix<-arima(a.2,order=c(1,0,0),method=ML)

> a.2.fix

> a.2.fix$aic

>Box.test(a.2.fix$residual,type=Ljung-Box,lag=15)

>install.packages(forecast)

> library(forecast)

> a.2.fix2<-Arima(a.2,order=c(1,0,2),method=ML)

> a.2.fix2

>Box.test(a.2.fix2$residual,type=Ljung-Box,lag=15)

>a.2.fore<-forecast(a.2.fix,h=5)

> a.2.fore

> plot(a.2,xlim=c(2000,2022),main=预测图)