基于差分方程求解法对防护服最佳厚度问题的研究

Study on the Optimal Thickness of Protective Clothing Based on Difference Equation Method

摘要: 本文针对防护服各层温度分布的问题，运用了热传导、差分法求解微分方程及网格搜索等理论或方法，构建了热传导、单目标优化及多目标优化等模型，综合运用了MATLAB及SPSS等软件编程求解，得出了各层温度分布与时间、位置、环境温度、厚度的关系。本文的特色体现在方法、编程、灵敏度分析或研究思路等上。

Abstract: In this paper, based on the temperature distribution of each layer of protective clothing, the theory or method of heat conduction and differential method for solving differential equations and grid search are used to construct models of heat conduction, single target optimization and mul-ti-objective optimization. MATLAB and SPSS are comprehensively applied. Software programming solves the relationship between temperature distribution of each layer and time, position, ambient temperature and thickness. The characteristics of this paper are reflected in methods, pro-gramming, sensitivity analysis or research ideas.

1. 引言

热防护服是对在工作环境为高温或超高温条件下的工作人员进行的安全保护，从而避免热源对人体造成伤害的各种保护性服装，具有阻燃性、拒液性、燃烧时无熔滴产生、遇热时能够保持服装的完整性和穿着舒适性等特性，用于石油、化工、冶金、造船、消防、国防以及有明火、散发火花、熔融金属和易燃物质的场所。目前发达国家普遍使用的高性能阻燃纤维织物，比其他阻燃织物性能优异，但研发成本昂贵，在国内很难大面积推广使用，所以当前国内防护服制造业所面临的主要问题就是从工艺上改进，缩短研发周期，提高性能，降低成本。

根据上述题目背景及数据，题目要求建立数学模型讨论以下问题：

1) 通过给定条件下的数据建立数学模型，计算温度分布，并生成温度分布的Excel文件。

2) 确定II层的最优厚度，确保工作60分钟时，假人皮肤外侧温度不超过47℃，且超过44℃的时间不超过5分钟。

3) 确定II层和IV层的最优厚度，确保工作30分钟时，假人皮肤外侧温度不超过47℃，且超过44℃的时间不超过5分钟。

2. 模型假设

1) 假设热传递沿皮肤方向垂直进行。

2) 假设服装阻挡了大部分的外界热辐射，热量在服装内部之间传递时可以忽略辐射。

3) 假设各层之间的空隙足够小，可以忽略热对流的影响。

4) 假设温度变化是连续的。

5) 假设外界温度为恒定值保持不变。

6) 假设室温为25℃。

假设服装层的接触面处是绝热的。

3. 符号说明

见表1。

Table 1. Symbol Description

表1. 符号说明

4. 模型的建立与求解

4.1. 温度分布数学模型的建立与求解

4.1.1. 基于温度分布的热传导模型建立

对于问题一，首先根据附件中提供的假人皮肤外侧温度数据绘制出时间温度图，如图1所示。

Figure 1. Temperature-time distribution of the outer skin

图1. 皮肤外侧温度-时间分布图

分析图1和表格中的数据可知在1644秒以前温度呈上升趋势，但速率逐渐变小。而1644秒以后，温度保持在48.08℃不变，因此我们选取前1644秒的数据利用最小二乘法进行拟合，拟合过程和结果如表2 (自变量为时间、因变量为温度)和图2所示。

因此，我们可近似得到假人皮肤外侧时间–温度的拟合关系式：

$y=1.744E-008*x^3-4.506E-005*x^2+0.039*x+36.049$

而我们知道温度的分布可以划分为时间分布和空间分布，因此我们以时间t为x轴，空间位置x为y轴，温度T为Z轴建立三维坐标系。其中x轴以高温作业服装第I层的外表面为坐标原点，服装内部为正方向，y轴以时间t增大的方向为正方向，最终构建出温度T的时空分布(图3)。

Table 2. Model summary and parameter estimation

表2. 模型汇总和参数估计

Figure 2. Fitting results

图2. 拟合结果

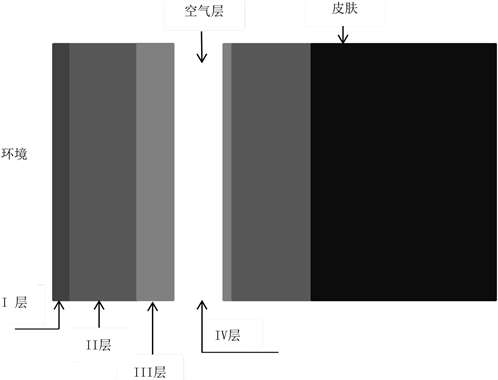
Figure 3. Protective clothing-skin system

图3. 防护服-皮肤系统

而查阅资料 [1] 可知，热量的传播主要靠热传导、热对流和热辐射三种形式(如图4所示)，但基于我们以上的假设，在服装层内部之间传递时，热对流和热辐射的影响可以忽略。

Figure 4. Three ways of heat transfer

图4. 热传递的三种方式

在热力学中，由以下两个物理定律和一个公式：

1) 傅里叶(Fourier)热传导定律

$dQ=-k\left(x,y,z\right)\frac{\partial u}{\partial n}\text{d}s\text{d}t$

2) 热量公式

$Q=cmu$

3) 热量守恒定律

温度变化吸收的热量 = 通过边界流入的热量 + 热源放出的热量可以得到热力学中的热传导方程

$\frac{\partial u}{\partial t}=div\left(Uu\right)=k\left(\frac{{\partial }^{2}u}{\partial x^2}+\frac{{\partial }^{2}u}{\partial y^2}+\frac{{\partial }^{2}u}{\partial z^2}\right)=k\left(u_{xx}+u_{yy}+u_{zz}\right)$

其中： $u=u\left(t,x,y,z\right)$ 表温度，它是时间变数t与空间变数此外，热传递由以下三种主要的方式：

鉴于假人内部的体温始终稳定在37℃，因此还应考虑人体作为热源对第IV层温度分布的影响(前三层可忽略)，最终，我们构建出温度分布的热传导模型为：

第一层： $C_{\text{I}}^A\frac{\partial T}{\partial t}\frac{\partial \left(K_{\text{I}}\frac{\partial T}{\partial x}\right)}{\partial x},x\in \left(0,0.6\right),t\in \left(0,t_{\exp }\right)$

第二层： $C_{\text{II}}^A\frac{\partial T}{\partial t}\frac{\partial \left(K_{\text{II}}\frac{\partial T}{\partial x}\right)}{\partial x},x\in \left(0.6,6.6\right),t\in \left(0,t_{\exp }\right)$

第三层： $C_{\text{III}}^A\frac{\partial T}{\partial t}\frac{\partial \left(K_{\text{III}}\frac{\partial T}{\partial x}\right)}{\partial x},x\in \left(6.6,10.2\right),t\in \left(0,t_{\exp }\right)$

第四层： $div\left(UT\right)+C_{\mathrm{IV}}^A\frac{\partial T}{\partial t}\frac{\partial \left(K_{\mathrm{IV}}\frac{\partial T}{\partial x}\right)}{\partial x},x\in \left(10.2,15.2\right),t\in \left(0,t_{\exp }\right)$

其中C^A表示显热容，单位kJ/(m³∙K)；T为温度，单位K；t为时间，单位s；x为水平坐标，单位m；k为热传导率，单位W/(m∙K)；t_exp = 1644 s；当环境温度变化幅度不大时，显热容C^A和热传导率k均近似看成常量，显热容的计算公式为：

$C^A=\rho c_p$

式中 $\rho$ 为对应织物的密度，单位kg/(m³)，c为对应织物的比热，单位J/(kg∙K)。

4.1.2. 热传导模型的求解差分方程法

本文采用有限差分方程法求解以多层高温作业防护服和人体皮肤为整体的偏微分方程组 [2] ，差分公式的推导如下

$T_{xx}\left(x_i-t_j\right)=\frac{T\left(x_i-h,t_j\right)-2T\left(x_i,t_j\right)+T\left(x_i+h,t_j\right)}{h^2}+o\left(h^2\right)\approx \frac{T_{i-1,j}-2T_{i,j}+T_{i+1,j}}{h^2}$

$T_t\left(x_i-t_j\right)=\frac{T\left(x_i,t_j+k\right)-T\left(x_i,t_j\right)}{k}+o\left(k\right)\approx \frac{T_{i,j+1}-T_{i,j}}{k}$

$\frac{T_{i,j+1}-T_{i,j}}{k}=\frac{T_{i-1,j}-2T_{i,j}+T_{i+1,j}}{h^2}$

$r=\frac{ck}{h^2}$

$T_{i,j+1}=\left(1-2r\right)T_{i,j}+r\left(T_{i-1,j}+T_{i+1,j}\right)$

其图解如图5所示：

Figure 5. Diagram of the difference method

图5. 差分法图解

根据我们的假设，由于I，II，III各层的初始温度为室温25℃，外界温度为恒温75℃保持不变且I层最外侧的温度等于外界温度，各层之间的接触面是绝热的，针对第I层我们可得到如下初始条件和边界条件：

初始条件：

$T\left(0,t\right)=75$

边界条件(绝热)：

$T\left(x,0\right)=25$

$T\left(x_0,t\right)=T\left(x_0,t-1\right)$

又根据热力学定律，虽然热量的扩散是混乱无序的，但是其在沿垂直皮肤方向的传播始终是沿x轴正方向(朝向皮肤)的，因此热量在这个方向分量可视为有序的。为了更好地体现出热量传播的过程，我们把I层作为起始层，从I层开始逐层向下求解，并将函数上一层的末态作为下一层的初态，直到第IV层为止，其思维逻辑图如图6所示：

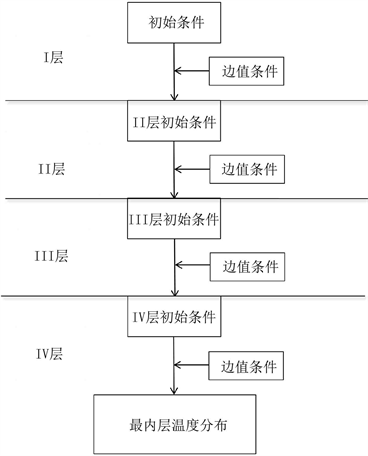
Figure 6. Solving the logic diagram of temperature distribution

图6. 求解温度分布逻辑图

递推公式：

$T{\left(x_0,t\right)}_{上一层}=T{\left(x_0,t\right)}_{下一层}$

由于各层厚度不一，而且各层之间相差较大，我们不能忽略厚度对热量传导的影响，因此我们考虑也把厚度作为热量传导方程模型的自变量，又因为厚度在这里可以表示为x轴的变化量，所以我们选取足够小的0.6 mm作为一个厚度单位，在此厚度中温度保持不变，这样每一层可划分为几个不同长度的单位，再分别对每个单位求出温度变化曲线。利用matlab求解，最终绘制出的温度时空分布图如图7所示：

并且由结果可知当趋于平衡时，I，II，III，IV层的温度分别最终稳定在72.91℃，66.33℃，58.78℃，50.22℃。

4.2. 问题二的求解

穷举法的基本思想是根据题目的部分条件确定答案的大致范围，并在此范围内对所有可能的情况逐一验证，直到全部情况验证完毕。若某个情况验证符合题目的全部条件，则为本问题的一个解；若全部情况验证后都不符合题目的全部条件，则本题无解。穷举法也称为枚举法。

首先明确，这是一个单目标优化问题。

根据分析，这里采用了遍历算法，即对II层的厚度范围进行遍历，然后根据差分法求解皮肤的温度时间分布，即得到一个递增序列，根据其判断是否满足题目要求，即是否符合60分钟内假人皮肤外侧不超过37℃以及超过44℃的时间不超过5分钟。只要符合要求，则找出一个最优解(最小厚度)。

Figure 7. Space-time diagram of temperature distribution

图7. 温度分布时空图

$\{\begin{array}{l}T=65˚\text{C}\\ \text{Thick}4=5.5\\ \text{Min}\left(\text{thick2}\right)\\ T\left(30\right)|{}_{x=\text{thick}1+\text{thick}2+\text{thick}3+\text{thick}4}<47˚\text{C}\\ |\{t{\left|T\left(t\right)\right|}_{x=\text{thick}1+\text{thick}2+\text{thick}3+\text{thick}4}>44˚\text{C}\end{array}$

这里由于是按照由小到大的顺序遍历厚度，则只要找到了符合要求的解，即可退出循环，返回结果。需要说明的是，这里虽然把II层厚度分为了100份，但事实上，根据差分法得到的皮肤层的T(t)是非递减的，只要第一次找到了符合条件的厚度值，其实就已经找到了解。详细流程如图8所示：

4.3. 问题三的分析和求解

给定条件下的II层、IV层最优厚度求解——基于贪心和穷举算法贪心算法(又称贪婪算法)是指，在对问题求解时，总是做出在当前看来是最好的选择。也就是说，不从整体最优上加以考虑，他所做出的是在某种意义上的局部最优解。

贪心算法不是对所有问题都能得到整体最优解，关键是贪心策略的选择，选择的贪心策略必须具备无后效性，即某个状态以前的过程不会影响以后的状态，只与当前状态有关。直观上看，本题属于多目标任务，即寻求一个最佳的II层和IV层的厚度的组合。但是经过分析，我们发现，在不考虑单位价格(事实上，条件的限制导致无法得出各层单位厚度的价格关系)的合理假设上，同时仅仅考虑重量，决策目标变为：

$\text{Min}\left(\text{thick}2+\text{thick}4\right)$

以下是基于程序暴力法和贪心算法的解法(图9)：

Ø Step 1：

以II层厚度d_ii作为外层循环，以IV层厚度d_iv作为内层循环。具体来说，就是遍历一遍所有可能的II、IV层厚度组合；

Figure 8. Problem 2 logic diagram

图8. 问题二逻辑图

这里以II层作为外层循环，第一次找到的解其实就是最优解。这是因为IV层其实是没有材质的，因此在考虑总重量的时候是无需考虑它的，然而鉴于体积太大也是个不利的影响。即重量的权重高于体积。

Ø Step 2：

将组合作为已知条件带入问题1中的四层热传递模型。在程序中的体现就是，将组合作为实参传入微分方程求解函数difference_equation。此函数将进行热能的层层传递，从而得到皮肤的温度时间图，并返回其对应的数组TEM4。这里有一个小技巧：在进行基于上的微分方程求解之前，先检查一下是否的组合会优于已知的最优组合：

$\begin{array}{l}\begin{array}{l}\text{If}\text{thick}2\left(i\right)+\text{thick}4\left(j\right)>\text{ans}32+\text{ans}34\hfill \\ --------*\hfill \end{array}\\ \text{Continue};\end{array}$

这是因为，求解微分方程的代价是很大的，而*式的判断并不依赖于微分方程的结果，因此，事先判断当前组合是否已经优于了已知的最优组合能够提高算法效率。

Ø Step 3：

此时已经从Step 2中得到了数组TEM4，并且当前组合已经优于了已知的最优组合，现在只需判断在此厚度组合下，能否满足

1) 30分钟以内，假人皮肤外侧温度不超过47℃，

2) 超过44℃的时间不超过5分钟。一旦满足，则更新当前最优解。

Figure 9. Solving process of problem 3

图9. 问题三求解过程

5. 模型的推广

本模型利用差分方程法直观形象地观察到在各层纺织材料之间的热传递以及温度变化，为提高热防护服装的性能以及降低研发成本提供理论依据。同时该模型还可以用来模拟燃料元件和包壳的温度分布，从而得出燃料和包壳的等效热阻和热容。应用该模型预测了织物层和皮肤层的温度随时间的变化规律，同时用其来预测各级高温服装层的温度分布情况，为实际的高温作业者提供有用的安全知识。

NOTES

^*第一作者。