1. 引言
近年来,越来越多的人开始关注整数阶Choquard方程
(1.1)
此外,也有很多人研究(1.1)式中
时的经典问题。当 ,
,
,
, 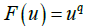 且
时,(1.1)式就会是著名的Choquard-Pekar方程
且
时,(1.1)式就会是著名的Choquard-Pekar方程
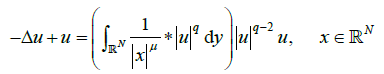 (1.2)
(1.2)
当
,
且
时的情况,是1954年Pekar在 [2] 中用来描述极化子静止时的量子理论时提出的。(1.2)式是1976年Choquard在 [3] 中描述单组分等离子体的Hartree-Fock理论时提出的。Lions在 [4] 中由临界点定理得到方程在
中有无穷多镜像解的存在性。对于基态解的一些性质,L. Ma和L. Zhao在 [5] 中证明了对于
时,广义的Choquard方程(1.2)式的每个正解都是径向对称的,并且单调递减到某一点。后来Moroz和Schaftingen在 [6] [7] 中消除了这种限制,并得出最佳参数的、基态的正则性和径向对称性,并推导出这些解在无限远处渐近衰减。还有一些人专注于半经典问题,即(1.1)式中的
。非局部问题(1.1)的半经典解的存在性已经在 [8] 中给出。
在证明解的存在性时,临界点理论是解决问题的基本工具之一。1978年P. H. Rabinowitz在文献 [9] 介绍了鞍点理论,这迅速成为临界点理论的基础,也是极大极小原理之一。Jonas Volek在文献 [1] 中提出,如果泛函满足P. H. Rabinowitz的鞍形假设,再满足PS紧性条件以及下方有界,就可以得出方程至少有三个临界点。到目前为止,人们主要研究关于整数阶Choquard方程解的存在性、多重性以及集中性,据我们掌握的文献来看,还没有人研究Choquard方程的三临界点问题。因此受文献 [1] 中方法的启发,本文就对如下整数阶Choquard方程进行研究
(1.3)
其中,
是具有光滑边界的有界开集,
,
,
,
,
。非线性函数
,
,在
时有
,且满足:
(f1)
.
(f2)
.
得出如下结论:
定理1.1 设
,存在
,
使得
,
时,方程(1.3)式至少有三个弱解。
2. 泛函设置
设
是具有光滑边界的有界开集,Sobolev空间
的范数为
Lebesgue空间
的范数为
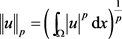
接下来介绍一些本文用到的结论。
引理2.1 (Hardy-Littlewood-Sobolev不等式) 令
且
使得
。若
且
。则存在一个与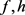 都无关的常数
,使得
都无关的常数
,使得
引理2.2 ( [1] , Theorem1.1) 设X是实Banach空间,
其中
维数有限。假设
有下界,并且满足
(R)
(PS) 对任意的序列
使得
有界,并且
有收敛子列。
则J至少有三个临界点。
经过计算可以推出方程(1.3)相应的能量泛函为
引理2.3 设
,则泛函J满足:
a)
并且满足
其中
。
b)
是(1.3)的弱解,当且仅当
是J的临界点。
由上述引理可知,想要证明定理1.1只需证明J有至少三个临界点。
引理2.4 设
则泛函J在
上弱强制,即当
时,有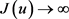 且J有下界。
且J有下界。
证明:根据(f1)以及(f2)可以得出,对任意的
存在
使得下式成立
(2.1)
根据(2.1)以及引理2.1,可以推出下面不等式成立
(2.2)
其中
。注意到
则有
,
。故结合(2.1)和(2.2)式可以推出
(2.3)
当
时,有以下两种情况:
i) 若
有界,则有
。
ii) 若
,则由
以及
可知~
。
故J是弱强制的。此外,由(2.3)式可推出
不等式右边是与
有关的函数,又因为
且
,所以不等式右边是有下界的,故出J有下界。
因为J是
且下方有界,由文献 [10] 知J存在PS序列。又因为J是弱强制的,所以PS序列
有界,因此有下面引理成立。
引理2.5 如果序列
有界且
,则
有收敛子列。
证明:由
有界可知,在子列意义下有
注意到
故
(2.4)
此外
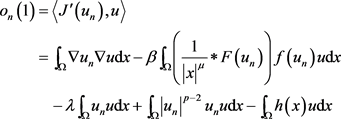
故
(2.5)
因为
有界,由(f1)-(f2),引理2.1以及Hölder不等式可得出
其中
。结合(2.4),(2.5)和(2.6)式可知
。又因为
于
,所以有
于
。
3. 定理1.1的证明
由引理2.4和引理2.5,我们有下面的引理成立。
引理3.1 设
,则泛函J满足PS条件,即引理2.2的条件(PS)成立。
接下来证明J至少存在三个临界点,设
为
中对应的特征值
(
算子的特征值)的特征函数且
是
的规范正交基(参见文献 [11] 的Thm. 2.2.16),并且
。将
分解为
,其中
(3.1)
引理3.2 设
,则存在
对任意的 且
,都有泛函J满足引理2.2中的条件(R),其中
满足(3.1)式。
且
,都有泛函J满足引理2.2中的条件(R),其中
满足(3.1)式。
证明:设
结合Parseval等式有下式成立
注意到
满足
(3.2)
因为
所以有
(3.3)
因此,对
由(3.3)以及嵌入定理可以得到
(3.4)
上式中
,其中
我们断言,存在
,当  时,
。又因为
且
,因此存在
,当
时,
。又因为
且
,因此存在
,当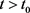 ,
时,有
,
时,有
则
的最小值只能在区间
上达到。因为
,所以存在
,当
时,对任意
有
(3.5)
所以
。当取
时,有下式成立
由
,以及(3.2)式可以推出
(3.6)
因此,对任意的
由Sobolev嵌入定理以及(3.6)有下式成立
(3.7)
因此,结合(3.5)和(3.7)式可知,如果要证明引理2.3中条件(R)成立,当且仅当存在
使得对
,
时要有下式成立
记
整理得出下式
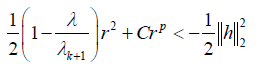
记
因为
与
无关,并且
。故存在某个
使得
为
的严格负的极小值。因此存在一个充分小的
使得
因此,对任意的
且
以及
且
有
因此满足引理2.2中的条件(R)。
综上所述,验证出引理2.2的所有条件都成立,所以泛函J至少存在三个临界点,即定理1.1成立。