1. 引言
无论从实验角度或是理论角度来看,氢原子与氢卤化物分子例如HF,HCl和HBr的碰撞在理解化学运动学和动力学中均扮演着非常重要的角色。由于Br原子包含了大量的电子,因此BrH2体系势能面的构建要比FH2或者ClH2体系更加困难。最近由于计算机的迅速发展,人们逐渐开始尝试利用实验和理论方法研究BrH2体系。大多数的实验聚焦在H + HBr反应的提取(H + HBr→H2 + Br)及交换(Ha + HbBr→Hb + HaBr)两个通道的反应速率常数。Aker等人利用相干反斯托克斯拉曼散射光谱(CARS)测定了在碰撞能为1.6 eV下提取通道的积分反应截面为3 ± 1 Å2,交换通道的积分反应截面为11 ± 2 Å2 [1]。实验还发现产物的量子态分布受势能面和动力学主导。运用适应光技术和准经典轨线(QCT)计算,Zare及其合作者发现在H + HBr提取反应中存在两种反应机制 [2]。最近他们利用离子成像方法研究了D + DBr反应,发现了对反应的贡献几乎可以忽略的非绝热通道的存在 [3]。理论方面,基于H2Br体系的不同势能面,科研工作者们对Br + H2及其逆反应的动力学进行了计算。H2Br体系的从头计算势能面的先驱工作是由Lynch等人利用多参考组态相互作用(MRCI)方法完成的 [4]。随后,他们在基态和第一电子激发态势能面上对H + HBr反应的速率常数和同位素效应开展了量子散射计算 [5]。Kurosaki和Takayanagi利用MRCI和完全活性空间自洽场(CASSCF)方法构建了两个全局势能面(分别为MB1和MB2),均对应Br + H2反应的最低三重态
1
2A
′ [6] [7] ,势能面的数据与实验值吻合的相对较好。最近,谢代前研究小组利用MRCI方法(包含戴维森修正)发展了H2Br体系一个新的势能面,基于该势能面利用量子含时波包方法计算的速率常数与实验值的吻合程度有较大幅度的提高 [8]。近年来,唐等人利用上述势能面对Br + H2反应开展量子计算,结果暗示MB2势能面能提供更多与实验吻合的数据 [9]。通过已有文献发现,大部分前期工作重点在于利用量子和准经典方法处理Br + H2及其逆反应H + HBr的动力学性质,然而目前人们很少关注它的同位素取代反应H + DBr。由于该反应极富动力学性质,因此我们认为需要进行更深入的研究,例如不同角动量和不同方位攻击角对反应过程的影响还不明确。为了解决该问题并获得更为清晰的物理图像,我们在0~2.0 eV碰撞能范围内利用准经典轨线方法在MB2势能面上对H + DBr反应进行了详细的动力学计算。
2. 计算理论
本文在MB2势能面上利用标准的准经典轨线(QCT)理论对H + DBr反应的两个通道进行研究,其中提取通道为H + DBr→HD + Br,交换通道为(H + DBr→D + HBr)。由于QCT理论在大量文献中已详细给出,并且根据已有研究表明QCT方法在处理大部分三原子体系反应是非常有效的,这里仅给出与本文相关的计算细节。在计算过程中利用数值积分的方法求解哈密顿运动方程,积分采用四阶Runge-Kutta-Gill法和Hamming修正的四阶Adams-Moulton预测校正法。反应物分子轴的初始取向和振动初相位利用Monte Carlo理论随机取样。计算条件如下:设定反应物分子DBr处于基态(v = 0, j = 0),碰撞能范围为0~2.0 eV,能量格点为0.1 eV,每个能量点计算5万条轨线。初始入射原子与靶分子之间的距离设置为15 Å,积分步长为0.1 fs,该时间数值足够小赖保证能量和角动量的收敛。在角动量J = 0和碰撞参数b = 0时,反应几率由PJ=0(Ecol) = NR/NT来确定,其中NR为反应的轨线数目,NT为计算的总轨线条数即5万。每条轨线的碰撞参数b通过b2在0到
范围内随机选取得到。为了计算不同角动量下的反应几率,利用
来确定碰撞参数b,其中μ和v分别表示H-DBr分子的约化质量和相对速率。当攻击原子撞击到靶分子时,如图1所示攻击原子轨迹路线与靶分子间连线所夹的角定义为攻击角θ。考虑到Br原子质量较大,因此连接点O靠近Br原子一侧。QCT方法一个重要的缺陷在于无法处理量子效应,因此在本文中我们舍弃了最终量子数小于零的那些轨线。

Figure 1. The definition figure of the attack angle
图1. 攻击角示意图
3. 结果与讨论
本文利用了MB2基态势能面12A′进行了全部计算。文献 [7] 中作者利用改进的过渡态理论(TST)计算得到的速率常数与实验值吻合较好。图2拟合了有自旋轨道耦合(SOC)和无自旋轨道耦合时共线构型下H + DBr→HD + Br的最小反应路径,其中反应物渐近线的能量设置为零。从图中可以看出,反应提取通道的势垒高度几乎不受SOC效应的影响。考虑SOC效应该反应过程放热约20 kcal/mol,比不考虑SOC效应要略高。在此势能面上没有发现势阱,当H原子共线接近靶分子DBr时早期势垒的高度约为1.53 kcal/mol,当H原子垂直呈T构型接近靶分子时势垒高约为21.12 kcal/mol。更多关于该势能面的拟合过程可参考文献 [7]。
为了验证QCT方法处理该反应的合理性和准确性,图3计算了该反应物分子处于基态(v = j = 0)时提取通道的积分反应截面,结果同时包含了QCT统计不确定性所产生的误差值。在图示中将QCT计算结果与其它已有的理论数据进行了比较 [10] [11] [12] [13]。从图中可以看出,利用相同的势能面进行的量子计算结果与本文QCT计算结果吻合的非常好。重要的是在更低能区,我们把本文计算结果与量子结果进行了对比。从内图可以看出QCT结果仍能与量子结果保持一致,这暗示了QCT无法处理的量子效应例如零点能和隧穿效应在该反应中并不明显。由于该势能面势垒的高度较小,因此积分截面几乎不存在阈值。积分截面数值在0.15 eV碰撞能下迅速增大到1.39 Ǻ2,然后在0.7~2.0 eV间逐渐减小,这种行为符合放热反应的特征。Aker及其合作者们曾利用CARS测定了提取反应在碰撞能为1.6 eV下的积分截面为3 ± 1 Ǻ2,然而测量过程中的不确定性达到±33%~50%。我们推断积分截面应低于2 Ǻ2从而接近本文的计算数值1.12 Ǻ2,这需要进一步的实验以及构建新的势能面得到更加准确的积分截面。

Figure 2. Minimum energy pathways of abstraction for the collinear configuration
图2. 提取反应共线构型下的最小反应路径

Figure 3. Comparison of integral cross section for abstraction between present work and other theoretical results in the text
图3. 本文的提取反应积分反应截面现在的成果与其它理论结果对比
图4计算了在总角动量J = 0,10,20,30,40以及反应物分子DBr处于基态时交换通道H + DBr→D + HBr的反应几率。不同角动量下的反应几率呈现相似的趋势即在路线上直线向上然后下坡形成产物HBr,这预示了在该反应中直接反应机制占据了主导地位。当J = 0时,反应几率存在阈值大约为0.47 eV,该数值与势能面交换通道势垒高度0.51 eV非常接近。一旦碰撞能越过势垒高度,反应立刻发生并且反应几率逐渐增大到较高的数值,这说明交换通道存在一个更大的接收锥。图4同时还显示,当总角动量增大时,能量阈值也逐步的向高能转移,这是由于逐渐增大的离心势垒造成的。
图5预测了在总角动量为J = 0,10,20,30,40时提取通道H + DBr→HD + Br的反应几率。从图中可以看出,由于势能面对应提取通道的势垒高度非常小约为0.066 eV,在低分波时每条曲线均不存在能量阈值。然而当分波数为J = 40时,反应几率出现一个较大的能量阈值约为0.5 eV。这可能是由于在高分波情形下,反应体系的有效势垒突然增大,导致反应在低能情况下无法进行反应。只有当能量足够高时,反应物原子才能越过势垒与反应物分子发生碰撞进而反应。

Figure 4. The reaction probabilities for exchange channel at different J values
图4. 不同角动量数值下交换通道的反应几率

Figure 5. The reaction probabilities for abstraction channel at different J values
图5. 不同角动量数值下提取通道的反应几率
由于依赖攻击角的反应几率包含了丰富的原子-分子反应的化学立体动力学信息,本文重点研究了攻击角对反应过程的影响。图6统计了H + DBr (v = 0, j = 0)→HBr + D反应碰撞能和攻击角依赖的反应几率。本文一个重要的发现为反应几率强烈依赖于攻击角。图示很明显可以看出,在低能情况下只有一个很小角度范围内(170˚~180˚)的攻击才能使得反应进行。然而在更高碰撞能下,反应可以在20˚~40˚以及100˚~180˚两个攻击角范围内进行。一旦碰撞能越过势垒,在攻击角为180˚时反应能够很容易地发生。逐渐增大碰撞能时,反应能够发生的攻击角范围逐渐增大。显然,H-Br-D线性构型是反应能够发生的最优化构型。换言之,反应优先发生在攻击原子H直接碰撞靶分子中的Br原子情况下。由于在不同攻击角度下势垒的高度不同,碰撞很难在其它角度范围内进行。反应能够发生的攻击角范围所对应的势垒高度大都低于碰撞能,因此入射原子有足够的能量爬上势垒进而与靶分子进行碰撞纠缠发生反应。

Figure 6. The attack angle dependent probability of exchange channel
图6. 交换通道攻击角依赖的反应几率
图7计算了H + DBr (v = 0, j = 0)→Br + HD提取通道碰撞能和攻击角依赖的反应几率。可以看出碰撞能对攻击角范围的影响并不大,0˚~40˚是使反应成功进行的攻击角范围。与图6相反,H-D-Br线性构型是提取反应进行的最优化构型。也就是说反应更倾向于攻击原子H直接碰撞DBr分子中的D原子进而形成产物HD分子。从图6和图7可以看出,当攻击角为30˚时交换通道和提取通道的反应竞争非常明显。在低碰撞能下,由于提取通道势垒较低提取反应占据反应的主导地位。然而一旦能量足够大超过势垒高度,交换反应很快占据了主导地位。碰撞能对两个通道反应几率的影响明显不同,它提高了交换反应的几率而抑制了提取反应的进行。
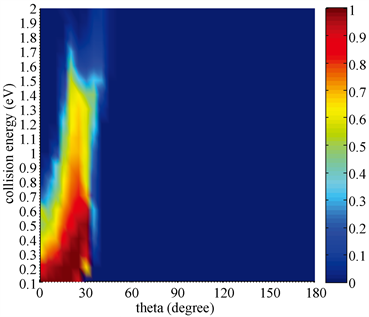
Figure 7. The attack angle dependent probability of abstraction channel
图7. 提取通道攻击角依赖的反应几率
4. 结论
本文利用准经典轨线理论在基态势能面上对H + DBr (v = 0, j = 0)反应进行了理论计算。由于势能面的势垒较小,因此反应几乎不存在阈值。在低能情况下,提取反应占据主导地位,然而一旦碰撞能越过势垒,交换反应迅速占据主导地位。随着总角动量的增加,由于离心势垒的增高,反应的阈值也随之增大。本文一个重要的发现为不同攻击角下的势垒高度不同,导致反应几率对攻击角度的依赖非常大。对于交换反应和提取反应而言,H-Br-D共线构型和H-D-Br共线构型分别为反应的最优化构型。
NOTES
*通讯作者。