Unity 3D中欧拉角与四元数关系的研究

Study on the Relationship between Euler An-gle and Quaternion in Unity 3D

摘要: 在Unity 3D游戏引擎中，物体的方位是用四元数的形式来存储的，但界面上给用户呈现的却是欧拉角。用户设置的欧拉角会先转化为四元数，最终转化为新的欧拉角，而每一个欧拉角都可以用两个四元数来表示，这样就会使问题变得非常复杂。本文给出了欧拉角的两种约定和欧拉角与四元数的数学表达式，通过对欧拉角和四元数在Unity3D游戏引擎中的实例应用的分析研究，将两者之间的转换关系做出了详细的说明。

Abstract: In unity 3D game engine, the orientation of objects is stored in the form of quaternions, but the Euler angle is presented to the user on the interface. The user-set Euler angle is converted to quaternion first and finally to a new Euler angle, and each Euler angle can be expressed in two quaternions, which makes the problem very complicated. In this paper, two conventions of Euler angle and mathematical expressions of Euler angle and quaternion are given. By analyzing and studying the application of Euler angle and quaternion in unity 3D game engine, the transformation relationship between them is explained in detail.

1. 引言

在Unity3D游戏引擎中，用方位来表征物体的旋转姿态，这是一个状态变量，方位可以采用旋转矩阵、欧拉角和四元数三种方法来描述 [1] 。在引擎中采用四元数来定义方位，但四元数不直观，设置困难，因此一般给用户呈现的是欧拉角。由于欧拉角可以任意设置，理论上同一个方位可以用无数个欧拉角来表示，也可以用两个四元数来表示。但Unity 3D引擎只用一个四元数来定义方位，这就造成了四元数与欧拉角一对多(1:n)的问题。采用四元数定义物体方位又带来另外一个问题，就是同一个方位可以用两个四元数来表示，这又形成了1:2的问题。因此同一个方位对应两个四元数和无数个欧拉角。用户为物体设置好的欧拉角会转化为系统内部的四元数，由系统内部的四元数又可以转化成一个新的欧拉角。因此转换过程是：用户设置欧拉角→系统内部四元数→新欧拉角。

虽然是同一个方位，但用户设置的欧拉角和系统生成的欧拉角在数据表现上并不相同，这会给学习Unity 3D游戏引擎带来巨大障碍，目前的各种文献都没有对此问题给出详细的介绍。本文从欧拉角和四元数的数学定义和转换公式入手，详细阐明其在Unity 3D中的基本原理，并通过具体实例讲解了两者的应用过程。

2. 欧拉角和四元数的概念

2.1. 欧拉角的概念

欧拉角是用来定义方位的一种表示，它有两种约定分别是“heading-pitch-bank”约定和“roll -pitch-yaw”约定。“heading-pitch-bank”约定是首先把物体坐标系和惯性坐标系对齐，物体旋转顺序为：y → x → z。heading是绕竖轴方向旋转，在Unity 3D中y轴竖直向上，因此heading是绕物体坐标系的y轴旋转。pitch是绕物体坐标系的x轴旋转，bank是绕物体坐标系的z轴旋转，如图1所示。

“roll-pitch-yaw”约定只考虑惯性坐标系，旋转的顺序为“roll-pitch-yaw”，即：z → x → y，与heading-pitch-bank (y → x → z)约定正好相反，如图2所示。

虽然heading-pitch-bank (y → x → z)约定与roll-pitch-yaw (z → x → y)约定相反，但这两种约定实质上是等价的。

2.2. 四元数的概念

四元数本身是一种超复数，用4个数来表示，形式为 $w+xi+yj+zk$，其中w为实部，x，y，z为虚部，满足 $i^2=j^2=k^2=ijk=-1$ [2] 。其中 $\left(x,y,z\right)$ 可以用一个三维向量来表示，即 $v=\left(x,y,z\right)$，设q为四元数，可表示为 $q=\left(w,v\right)$。在Unity 3D中习惯将四元数的实部写在后面即 $q=xi+yj+zk+w$，或 $q=\left(v,w\right)$。

Figure 1. Heading-pitch-bank

图1. 偏航角–俯仰角–滚转角

Figure 2. Roll-pitch-yaw

图2. 滚转角–俯仰角–偏航角

3. 欧拉角与四元数的转换

3.1. 从欧拉角转换到四元数

物体某一方位可以用欧拉角 $\left({\theta }_h,{\theta }_p,{\theta }_b\right)$ 来表示，也可以用一个四元数 $q=w+xi+yj+zk$ 来表示，该四元数q可以用 $q_h,q_p,q_b$ 来表示。 $q_h,q_p,q_b$ 分别为绕轴y，x，z旋转的四元数。在此使用负旋转量。

$q_h=\left[\begin{array}{c}\cos \left({\theta }_h/2\right)\\ \left(\begin{array}{c}0\\ -\sin \left({\theta }_h/2\right)\\ 0\end{array}\right)\end{array}\right],q_p=\left[\begin{array}{c}\cos \left({\theta }_p/2\right)\\ \left(\begin{array}{c}-\sin \left({\theta }_p/2\right)\\ 0\\ 0\end{array}\right)\end{array}\right],q_b=\left[\begin{array}{c}\cos \left({\theta }_b/2\right)\\ \left(\begin{array}{c}0\\ 0\\ -\sin \left({\theta }_b/2\right)\end{array}\right)\end{array}\right]$

$q_h,q_p,q_b$，是三次旋转，最终需要形成一个四元数q，将三者直接相乘即可，即 $q=q_h{q}_p{q}_b$，矩阵相乘的顺序采用“heading-pitch-bank”约定。

则 $q=q_h{q}_p{q}_b=\left[\begin{array}{c}\cos \left({\theta }_h/2\right)\cos \left({\theta }_p/2\right)\cos \left({\theta }_b/2\right)+\sin \left({\theta }_h/2\right)\sin \left({\theta }_p/2\right)\sin \left({\theta }_b/2\right)\\ \left(\begin{array}{c}-\cos \left({\theta }_h/2\right)\sin \left({\theta }_p/2\right)\cos \left({\theta }_b/2\right)-\sin \left({\theta }_h/2\right)\cos \left({\theta }_p/2\right)\sin \left({\theta }_b/2\right)\\ \cos \left({\theta }_h/2\right)\sin \left({\theta }_p/2\right)\sin \left({\theta }_b/2\right)-\sin \left({\theta }_h/2\right)\cos \left({\theta }_p/2\right)\cos \left({\theta }_b/2\right)\\ \sin \left({\theta }_h/2\right)\sin \left({\theta }_p/2\right)\cos \left({\theta }_b/2\right)-\cos \left({\theta }_h/2\right)\cos \left({\theta }_p/2\right)\sin \left({\theta }_b/2\right)\end{array}\right)\end{array}\right]$ (1)

3.2. 从四元数转换到欧拉角

根据上面的公式(1)，如果已知左侧的四元数q就可以求出右侧的欧拉角 $\left({\theta }_h,{\theta }_p,{\theta }_b\right)$，结果如下：

${\theta }_p=\text{asin}\left(-2\left(yz+wx\right)\right)$

${\theta }_h=\{\begin{array}{l}\text{atan}2\left(xz-wy,1/2-x^2-y^2\right)若\cos p\ne 0\\ \text{atan}2\left(-xz-wy,1/2-y^2-z^2\right)其他\end{array}$ (2)

${\theta }_b=\{\begin{array}{l}\text{atan}2\left(xy-wz,1/2-x^2-z^2\right)若\cos p\ne 0\\ 0其他\end{array}$

4. 在Unity 3D中欧拉角和四元数的应用

四元数本质上是一个角轴对，即物体绕着某一个轴旋转一定的角度 [3] 。如图3所示，是物体的所处的一个状态，轴向量为 $n=\left(0.\text{3},0.\text{9},-0.\text{2}\right)$ 和角θ = 73.2˚。

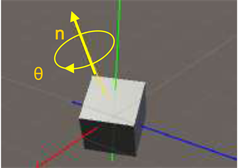
Figure 3. Determination of object orientation by angular pair

图3. 角轴对决定物体方位

已知轴的方向n，那么绕这个轴旋转θ角，可以是0˚、30˚、90˚、180˚、360˚、720˚等。0˚是指物体坐标系和惯性坐标系重合的状态。

轴可以是任意的，下面是四元数 $q=\left(x,y,z,w\right)$ 与角轴对 $\left(\theta ,n\right)=\left(\theta ,n_x,n_y,n_z\right)$ 之间的关系：

$q=\left(x,y,z,w\right)=\left(n_x\sin \left(\theta /2\right),n_y\sin \left(\theta /2\right),n_z\sin \left(\theta /2\right),\cos \left(\theta /2\right)\right)$

当θ = 0时， $q=\left(0,0,0,1\right)$。因为 $\text{sin}\left(\theta /2\right)=0$，所以有 $n=\left(n_x,n_y,n_z\right)$，可以是任意轴。

其中 $q=\left(0,0,0,1\right)$ 这个四元数的含义是不旋转。其地位相当于实数中的1，或矩阵中的单位阵。任何四元数与该数相乘保持不变。在Unity3D中对这个四元数有专门的定义：

Quaternion.identity

因为四元数每个分量的取值范围是[−1, 1]，因此当用户给出不同的欧拉角时，系统会根据用户给出的欧拉角进行计算 [4]，得到相应的四元数。例如当旋转轴保持为竖直方向的y轴时，即 $n=\left(0,\text{1},0\right)$。θ = 0时的四元数为 $q=\left(0,0,0,1\right)$，当θ = 360˚时，四元数为：

$q=\left(0\sin \left(360/2\right),1\sin \left(360/2\right),0\sin \left(360/2\right),\cos \left(360/2\right)\right)=\left(0,0,0,-1\right)$

从欧拉角来看，0度和360度是同一状态，然而却对应着不同的四元数，如表1所示是欧拉角与四元数的一个对应关系。

Table 1. Initial Euler angle, quaternion and final Euler angle

表1. 初始欧拉角，四元数与最终欧拉角

在Unity 3D中，由欧拉角生成四元数的代码：Quaternion q = Quaternion.Euler (0, 90, 0)；由四元数生成欧拉角的代码：Vector3 v = q.eulerAngles。

表中第一列是用户给定的欧拉角，由此欧拉角生成四元数列于第二列，根据四元数再生成欧拉角列在第三列，即Vector3 v。从表中可以看出，从0˚到360˚再到720˚，四元数的实部从1到0到−1再到0再到1，也就是欧拉角转两周，四元数回到初始值。因此同一个欧拉角会有两个四元数与之对应，因为同一个状态可以沿旋转轴正向旋转，也可以反转到同一状态，可以认为将轴的方向反向 [5] 。

5. 分析及总结

本文介绍了欧拉角和四元数的概念，以及两者之间的转换关系，又通过实例数据解释说明了欧拉角和四元数在Unity3D中的存在形式和联系，以利于Unity3D使用者更好的理解旋转操作。