1. 引言
数据融合 [1] 技术是一种多传感器信息数据处理的技术,它利用计算机技术,对来自各个传感器的信息数据在一定的方法下,加以分析、提取、综合,得到被测对象更加全面、可靠、准确的结果。
多传感器数据融合可以增加测量的可信度,改善系统的可靠度,在工业和军事等方面得到了广泛的应用。本文利用多元统计方法中的主成分分析法计算测量值与主成分的相关系数,得出各传感器的综合支持程度,剔除综合支持程度较低的数据,对于剔除后的有效数据,首先将测量与估计值都进行模糊化,然后计算测量值与估计值之间的模糊贴近度,利用贴近度来描述各个传感器的重要度,确定各个传感器在融合算法中的权重。最后利用融合公式求出融合结果。
2. 主成分分析法
主成分分析法 [2] 是将研究对象的多个相关变量(指标)化为少数几个不相关的变量的一种多元统计方法。它作为一种数据分析技术,能对原有数据集进行简化处理,有效找到其中最主要的元素和组成结构,同时剔除信息中的噪音,降低数据冗余性,还能将原有的复杂数据进行降维处理,使得复杂数据结构能够简单化。主成分分析 [3] 的主要内容是把多个变量综合成一个或者少数几个综合指标,通过使用少数的综合指标来代表尽可能多的变量所包含的信息。
定义1:设总体
的协方差阵为
,其特征根为
,对应的单位化正交特征向量为
,其中
,则第i个主成分为:
(1)
定义1中,当总体的协方差未知时,可以用样本的协方差矩阵或相关矩阵代替。
定义2:在主成分分析中,定义主成分
的方差贡献率
(2)
来说明各主成分
概括原变量X信息的大小。称
为前k个主成分的累计方差贡献率。一般情况下取k使得累计方差贡献率
达到85%以上。
定理1:总体X的原变量
与主成分
的相关系数为
(3)
其中,
为
的标准差,
为特征向量
的第j个分量。
定理2:设
为总体X的前k个主成分,则
与
的复相关系数的平方:
(4)
因为
表示k个主成分
对原变量
的贡献率,而这k个主成分
概括了原变量X的85%以上的信息,所以在某种程度上,
可以看成是在总体X信息中所在的比重,可以利用
来定义各传感器的综合支持程度。
定义3:定义第i个传感器的综合支持程度:
(5)
累计综合支持程度越高,则所包含的信息比重越大,一般情况下,取累计综合支持程度达85%以上的传感器。
3. 模糊数学
基于模糊贴近度的数据融合算法 [4] 先将传感器量测值与目标估计值进行模糊化,再定义与计算每个传感器的量测值模糊量与目标估计值模糊量之间的贴近度。由贴近度的大小来表示传感器的重要性,贴近度越大表示该传感器对数据融合结果的影响越重要,在融合过程中其权重也越大。最后提出数据融合公式实现多传感器数据融合。
对于第i个传感器,设其对真实值A的m次测量后的测量均值为
,测量方差为
。则量测值的模糊量表示为
(6)
定义
与
的贴近度为
(7)
其中
第i个传感器权重
为:
(8)
将它们归一化后可以得到各个传感器之间的相对权重为:
(9)
则融合结果为:
4. 应用实例
秭归县白水河滑坡8个传感器在2009年~2011年期间,水平位移监测值见图1。ZG91,ZG92,ZG93,ZG94,ZG118,ZG119,ZG120,XD01,8个传感器在秭归县白水河测得2009年1月到2011年12月的水平滑坡位移监测值 [5] ,通过数据融合的到最后融合数据,以此判断秭归县白水河的滑坡情况。
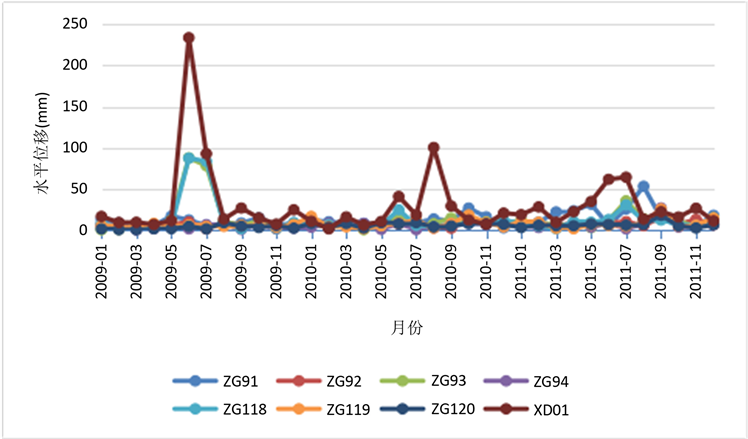
Figure 1. Displacement monitoring curve of baishuihe landslide
图1. 白水河滑坡水平位移监测曲线
对于秭归县白水河滑坡8个传感器在2009年~2011年每月的水平位移监测值,运用主成分分析法可知,上面8个传感器的综合支持度分别为0.024,0.022,0.047,0.058,0.064,0.118,0.331,0.358,则根据累计综合支持度大于85%,ZG91、ZG92、ZG93、ZG94的综合支持度不够,融合时删其读数,取其余传感器的测量数据用模糊贴近度的数据融合算法进行融合。传感器个数
,测量次数
。模糊数学和主成分与模糊数学融合所得的结果见表1。


Table 1. Compared the results of data fusion
表1. 数据融合结果比较
由表1可以看到,本文提出的主成分与模糊数学方法与模糊数学融合结果相比,在计算过程中,由于用主成分减少了4个综合支持度不高的数据,在后面用模糊数学融合时,计算量少了很多。
5. 总结
多传感器数据融合综合利用多种传感器的信息以获得有关目标的属性特征,可以避免单一传感器的局限性限制,减少各传感器不确定误差的影响。本文提出了一种基于模糊理论与主成分分析方法集成的多传感器数据融合算法,该方法计算过程相对固定,便于计算机实时实现。