基于部分充电策略的电动物流车配送路径优化

Electric Vehicle Routing Problem Based on Partial Recharging Strategy

摘要: 随着电子商务的不断发展，物流需求呈现爆发式的增长，客户订单呈现出多批次、少批量的特点。针对之前电动物流车路径问题中完全充电策略假设的不足之处，本文统筹协调电动物流车路径及充电决策，构建了更加接近实际情况的部分充电策略下的电动物流车配送路径优化模型，并设计遗传算法进行求解。实例计算结果表明，与完全充电策略相比，基于部分充电策略能够有效降低车辆路径成本。

Abstract: With the continuous development of e-commerce, logistics demand has experienced explosive growth, and customer orders have been characterized by multiple batches and small batches. This paper co-ordinates the route and recharging strategies of electric vehicles (EVs); it is different from the basic assumption of full recharging in the previous E-VRP; we model an E-VRP with partial recharging based on the actual situation. The calculation results of an example shows that compared to the full recharging strategy, the vehicle routing cost based on the partial recharging strategy can be reduced effectively.

1. 引言

随着环境污染、能源消耗问题的日益严重，传统燃油车逐渐被新能源汽车替代。国家各部门相继出台了一系列政策法规来推进电动汽车的使用。例如我国交通部在2014年发布的《关于加快新能源汽车推广应用的实施意见(征求意见稿)》 [1] 中明确指出，到2020年，我国新能源城市物流配送车辆应达到5万辆，同时要求地方政府在充电站等基础配套设施的建设上，对新能源城市物流配送运输予以优先考虑。国内目前许多大型的电商企业，例如京东、苏宁等行业领导者都先后购入电动汽车进行配送。

而近年来电子商务的迅速发展使物流网络不断扩大，对企业来说，单纯的降低配送成本将对企业发展产生不利影响。车辆充电决策及路径的选择都会对电动物流车配送成本产生影响。配送途中，不考虑充电量的决策，会增加车辆充电成本、充电时间并降低充电的灵活性。完善的配送路径规划需要将这些问题统筹兼顾，通过科学的规划方法使最终的电动物流车配送成本最低。

2. 相关研究评述

车辆路径问题是物流领域一个重要的研究方向，1959年，Dantzig和Ramser [2] 首次提出了车辆调度问题，他们模拟了一系列同质卡车如何从枢纽中心以最小的行驶距离来满足多个加油站的石油需求。五年后，Clarke和Wright [3] 将这个问题一般化为线性规划问题，也就是我们现在所熟知的传统车辆路径规划问题。

之后，随着新能源汽车的推广使用，相关学者开始研究电动物流车路径问题。Schneider，Stenger [4] 首次研究了在配送途中有独立的充电站能够进行充电的电动汽车路径问题。在该文献中，车辆能够在特定的充电站补充电量，且充电时间与消耗能量成线性相关的关系。在Solomon [5] 算例及之前学者实例的基础上提出了新的标杆问题，采用可变领域搜索的启发式算法，得到了更优的结果。与之前基础的电动汽车路径问题研究不同，这篇文献中，充电时长不是一个固定的数值，而是与补充的电量呈线性关系。这更加接近实际情况，也为之后的研究奠定了基础。Matin M [6] 构建了一个模型用于解决带有时间窗及充电站容量约束的电动汽车路径问题，根据车辆属性及相关数据，确定了完成配送任务所需的最佳车辆数量及充电站的数量。

考虑到电动汽车充电给电网造成的巨大压力，我国充电桩的电价通常采用分时定价的方法进行收费。孙晓明 [7]、张静 [8]、严俊 [9]、李明 [10] 等人研究了基于分时电价的电动汽车路径选择与充电导航策略，相关研究结果有助于提高用户出行效率并缓解大规模无序充电对配电系统安全运行的影响。

目前在物流配送中，相比传统燃油车，电动物流车路径优化问题的求解难度更大，充电决策也会对整个路径产生重要影响。因此，更加合理高效的路径规划在解决电动物流车配送问题中是十分必要的。本文提出在基于部分充电策略的电动物流车配送路径优化方法。

3. 问题描述及求解思路

基于以上分析，本文在传统车辆路径问题的基础上，综合考虑纯电动物流车的技术特征，提出了具有行驶里程及车载容量限制的电动物流车配送路径优化问题。问题具体描述为：某公司拥有一个城市配送中心，配送中心内有多辆纯电动物流车为多个客户提供配送服务。每个客户位置及需求量已知，仅可被访问一次。车辆以满电状态从配送中心出发，配送途中，若电动物流车剩余电量不足以完成后续的配送任务，可到最近的社会充电设施进行充电，充电次数及每个充电站被访问的次数都没有限制，本文目的是通过合理的安排配送路线、出行时间及充电计划，达到运营成本最小的目标。

3.1. 基本假设

为将实际问题进行合理简化，本文进行如下假设：有且仅有一个配送中心，电动物流车从配送中心出发，最后再返回配送中心；配送中心只有一种型号的纯电动物流车，车辆具有载重限制，车辆从配送中心出发时为满电状态，充电时不考虑充电等待时间；客户的需求量及位置已知，且需求不可拆分；充电站的位置已知，充电站内充电桩的相关参数均相同；车辆行驶速度恒定；电量消耗与行驶距离、充电时间与充电量呈线性相关关系；车辆服务过程中没有电量消耗。

3.2. 变量与参数定义

为了清晰的构建E-VRPTW问题，本节将模型中涉及到的变量及参数定义列于表1中，其中决策变量为x_ij、z_i、T_i、Z_i。

Table 1. Relevant variables and parameter descriptions

表1. 相关变量及参数说明

3.3. 数学模型

Min

$c_f{\displaystyle \underset{i\in V^{\prime }}{\sum }{x}_{oi}}+c_t{\displaystyle \underset{i\in {V^{\prime }}_o}{\sum }{\displaystyle \underset{j\in {V^{\prime }}_{N+1}}{\sum }{t}_{ij}{x}_{ij}}}+c_q{\displaystyle \underset{j\in R^{\prime }}{\sum }{t}_j^q}+c_g{\displaystyle \underset{j\in R^{\prime }}{\sum }\left(Z_j-z_j\right)}$ (1)

Subjectto

${\displaystyle \underset{j\in {V^{\prime }}_{N+1},i\ne j}{\sum }{x}_{ij}}=1\forall i\in V$ (2)

${\displaystyle \underset{j\in {V^{\prime }}_{N+1},i\ne j}{\sum }{x}_{ij}}\le 1\forall i\in R^{\prime }$ (3)

${\displaystyle \underset{i\in {V^{\prime }}_0,i\ne j}{\sum }{x}_{ij}}-{\displaystyle \underset{i\in {V^{\prime }}_{N+1},i\ne j}{\sum }{x}_{ji}}=0,\forall j\in V^{\prime }$ (4)

${{\rm T}}_i+\left(t_{ij}+s_i\right)x_{ij}-l_0\left(1-x_{ij}\right)\le {{\rm T}}_j\forall i\in V_0,\forall j\in {V^{\prime }}_{N+1},i\ne j$ (5)

${{\rm T}}_i+t_{ij}{x}_{ij}+\theta \left(Z_i-z_i\right)+t_i^q-\left(l_0+\theta Q_{\max }\right)\left(1-x_{ij}\right)\le {{\rm T}}_j\forall i\in R^{\prime },\forall j\in {V^{\prime }}_{N+1},i\ne j$ (6)

$e_i\le {{\rm T}}_i\le l_i\forall i\in {V^{\prime }}_{0,N+1}$ (7)

$0\le z_j\le z_i-\left(e\cdot d_{ij}\right)x_{ij}+Q_{\max }\left(1-x_{ij}\right)\forall i\in V_0,\forall j\in {V^{\prime }}_{N+1},i\ne j$ (8)

$0\le z_j\le Z_i-\left(e\cdot d_{ij}\right)x_{ij}+Q_{\max }\left(1-x_{ij}\right)\forall i\in {R^{\prime }}_0,\forall j\in {V^{\prime }}_{N+1},i\ne j$ (9)

$z_i\le Z_i\le Q_{\max }\forall i\in {R^{\prime }}_0$ (10)

$x_{ij}\in \left\{0,1\right\}\forall i\in {V^{\prime }}_0,j\in {V^{\prime }}_{N+1},i\ne j$ (11)

其中，目标函数(1)最小化总成本，包括固定成本，旅行成本，排队成本和再充电成本。约束(2)确保每个客户只被访问一次。约束(3)表明车辆最多可以访问每个充电站(包括虚拟顶点)一次。约束(4)为节点车流量进出平衡约束。约束条件(5)和(6)分别表示离开客户(和仓库)和充电站的时间。约束(7)表示客户和仓库的时间窗口。约束(8)和(9)分别定义当车辆离开客户(和仓库)和充电站时的电池水平，并确保其不会为负。约束(10)表明电池电量不能超过其额定电量。约束(11)定义了0-1决策变量，它决定车辆形式路径。

4. 实验结果及分析

为验证本文所提出的基于客户分组的电动物流车路径优化模型及算法的有效性，本文选择北京市A公司作为研究案例，A公司是国内某大型电商企业，目前已将B2B业务中传统的燃油配送车替换为电动物流车，其B2B业务的客户主要集中在北京市五环之内。因此本文收集A公司某天的小B端订单作为研究对象。对位于配送中心旁边的客户点，默认为无需进行配送路径规划，将其舍去，对货运量很大，达到或超出一辆车载重的客户节点也将其舍去。最终选取货运量较小，需要进行配送路径规划的客户点，按照本文配送方案规划思路计算得到针对该公司配送中心的车辆路径规划结果，并对结果进行比较分析。

4.1. 原始数据处理

按照本文配送方案规划思路对客户进行车辆配送路径规划。所选取配送部分客户订单数据如表2所示：

Table 2. Customer information

表2. 客户点信息

本文设定A公司所用电动物流车额定载重量为1.5 t，平均行驶速度为45 km/h，平均服务时间18分钟。此外，电池额定电量为60 kWh，单位里程平均能耗为0.4 kWh/km，服务过程中车辆不消耗电量；充电时间与充电量呈线性相关关系，平均充电速度为30 kWh/h，快速充电模式下充电成本约为2元/kWh (包括电费和服务费)。

4.2. 计算结果及分析

本文设置初始种群数为200，交叉和遗传分别为0.8和0.05，设置最大迭代次数为1000，惩罚系数c_e = 60，c_l = 60。得到部分充电与完全充电策略下电动物流车的路径结果分别如表3和表4所示：

Table 3. Optimal routes and costs of groups with partial recharging

表3. 部分充电策略下各组最优配送路径及成本

Table 4. Optimal routes and cost of each group with full recharging

表4. 完全充电策略下各组最优配送路径及成本

根据计算结果可以得到如下结论：

与完全充电策略相比，部分充电策略下，车辆总行驶里程减少2.4%，但总成本降低12%。通过路径结果可知：在完全充电策略下，车辆每次的充电量大，因此会出现在一组客户中车辆进入充电站充电次数较部分充电策略下少的情况，因此最终完全充电策略下车辆的行驶距离小于部分充电策略下的行驶距离。但由于部分充电量少，充电时间灵活，因此最终得到的结果中部分充电策略下的总成本比完全充电策略下低。

4.3. 灵敏度分析

通过以上结果可知，电动物流车配送成本主要由时间成本及能源成本构成，影响成本的主要因素有充电量及充电时间。因此本文选取电池容量与充电率两个因素进行灵敏度分析。

4.3.1. 电池容量灵敏度分析

本文将电池容量在80 km的基础上分别增加至100 km、120 km、140 km、160 km，配送成本分别降低8.6%、15%、23.6%、29%。各组成本的详细变化情况如图1所示：

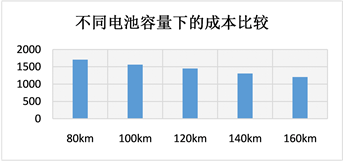
Figure 1. Routing cost under different battery capacity

图1. 不同电池容量下的路径成本

从上述结果可以看出，电动物流车的续航里程越长，中途需要的充电次数和充电量越少。配送所需的时间和平均行驶里程减少，配送成本降低的同时能够通过更好的满足客户的时间窗而提高客户的满意度。

4.3.2. 充电速率对路径优化的影响

为研究充电速率对路径成本的影响，本节将充电率设为相对初始值逐渐增加0%，100%，200%，即0.3、0.6、0.9。

Table 5. Routing costs at different recharging rates

表5. 不同充电率下的路径成本

从表5中，可以看出随着充电速率的增大，企业配送中惩罚成本呈减少的趋势，由于充电率与充电时间的长短有关，充电率的增大会减少充电时间，因此车辆在高充电率下能够减少惩罚成本。

5. 结论

本文在现有研究的基础上，提出基于部分充电策略的电动物流车配送路径优化方法。构建了基于部分充电策略的路径优化模型，并设计遗传算法进行求解。通过对实例的求解分析，验证了本文中所提出的模型及算法的有效性。但本文研究还存在许多不足之处，还有待于做更加深入的研究。如基于动态交通网络或客户动态需求进行更加接近实际情况的研究。

致谢

本论文是在我导师的悉心指导下完成的，感谢导师从论文的选题、结构调整到模型的构建和调整等方面的宝贵意见！同时感谢同师门的师兄师姐在我的学业中给予的支持和帮助。