江苏省5A级景区旅游路线规划

5A Level Scenic Spot Tourism Route Planning of Jiangsu Province

摘要: 本文借助著名的旅行商(TSP)问题对江苏省23家5A级景区旅游路线进行动态规划。首先确定了景点和所在市之间的交通数据，构建高铁和公交车联合的复杂的交通线路网络，建立最短路径模型。然后利用蚁群算法对模型进行优化和求解，再根据结果对蚁群算法进行改进，得到满足条件的最短路径规划模型，得到了最佳的旅游路线。

Abstract: In this paper, the famous TSP problem is used to study the dynamic planning of tourism routes, a large number of literatures are referred in detail, and the data of 5A scenic spots in Jiangsu Prov-ince are collected and studied. The traffic data between the scenic spot and the city are determined, the complex traffic line network combined by high-speed rail and bus is constructed, and the shortest path model is established. At the same time, the ant colony algorithm is used to optimize and solve the model, and the ant colony algorithm is improved according to the results to obtain the shortest path planning model that meets the conditions, so as to provide route selection for more self-help travelers.

1. 引言

旅游业是世界经济中持续高速稳定增长的重要战略性、支柱性、综合性产业，且旅游业具有“无烟产业”和“永远的朝阳产业”的美称，可以同时满足发展经济和保护环境 [1] 。中国幅员辽阔、历史悠久、山川秀丽形成了得天独厚的旅游资源，本文以江苏省5A级景区为例，建立路径最短模型，再利用智能算法中的蚁群算法来求解得出结论。为很多自助游人规划旅游路径提供便利，做到了在满足旅游者需求的前提下，降低成本，提高旅游效益。

2. 相关研究综述

2.1. 江苏省5A级景区概述

江苏省作为中国吴越文化的发祥地，这里有着历史悠久的园林建筑，古色古香的工艺品。从2007至今，江苏省有23家被评为国家5A级景区，分别是苏州园林；苏州昆山周庄古镇景区；南京钟山–中山陵风景名胜区；中央电视台无锡影视基地三国水浒城景区等。

2.2. 江苏省5A级景区的数据信息

为了更好对江苏省5A级景区做规划，我们从江苏省旅游官网整理了各个景区的门票和对应的城市为等级的住宿费(以经济酒店为主)如表1所示，再通过百度地图和12306网站得到两个景区之间的距离和动车费用如表2所示。

Table 1. Tickets and accommodation fees for 5A scenic spots in Jiangsu Province

表1. 江苏省5A级景区的门票和对应住宿费

Table 2. The distance between some scenic spots

表2. 部分景区之间的路程

3. 旅游路线的数学模型规划

3.1. TSP模型问题

TSP问题 [2] 从描述上来看是在给定n个城市和各城市之间的距离的条件下，寻找一条遍历所有城市的最短路径，并且保证每个城市只被访问一次。针对江苏省的5A级景区的旅行路线规划，它的要求主要有：1、每一个景区仅游览一次；2、不含子巡回；3、整个旅游费最合理，4、旅游路线最短。

3.2. 模型假设

1) 假设任意两个风景区都有便捷的公路；

2) 不考虑浏览风景区的先后顺序；

3) 假设旅游费用不包括餐饮，不考虑其他省到达江苏省的费用；

4) 只考虑经济酒店，不考虑节假日带来的单位住宿费的提高；

5) 不区分高速公路和普通公路；

6) 假设在旅途中只有高铁或自驾两种交通工具，公交车的计费方式为路程乘以单位耗油费，并且在旅途中尽量以乘坐高铁为主，公交车为辅。

3.3. 符号说明

1) $scene=\left\{1,2,\cdots ,23\right\}$ 表示风景区集合，其中1代指出发地；

2) $d_{ij}$ 表示风景区和风景区两地之间的距离；

3) $p_{ij}$ 为二值变量，表示路线中风景区j紧随取值1，否则为0；

4) PZ是乘坐过公交车程中的费用；

5) PG是旅游过程中乘坐高铁的票价；

6) $Qidia{n}_i$ 乘坐高铁的起始位置；

7) $Zhongdia{n}_i$ 乘坐高铁的终点位置；

8) $P_n$ 是公路上行驶的单位里程耗油费(0.6672元/公里)；

9) PL是对应城市等级的单位住宿费；

10) PM是对应旅游景区的门票费用；

11) $N{L}_{i,j}$ 对应城市的住宿费次数；

12) $D{T}_{i,j}$ 是第i次旅游路线中在普通公路或高数公路上行驶的里程；

3.4. 模型建立

3.4.1. 目标函数一：最短路径

$\min z={\displaystyle \underset{i}{\overset{n}{\sum }}{\displaystyle \underset{j}{\overset{n}{\sum }}{d}_{ij}{p}_{ij}}},\text{s}\text{.t}\text{.}$ (3.1)

约束条件：

$\forall j\in scene:{\displaystyle \underset{i\in scene}{\sum }{p}_{ij}}=1$ (3.2)

$\forall i\in scene:{\displaystyle \underset{i\in scene}{\sum }{p}_{ij}}=1$ (3.3)

$\forall i,j\in scene:p_{ij}\in \left\{0,1\right\}$ (3.4)

$v_i-v_j+np\le n-1,v_i,v_j\ge 0,i=1,2,\cdots ,n,j=2,3,\cdots ,n且i\ne j$ (3.5)

$v_i\le n-1,v_i取整数$ (3.6)

其中对于(3.1)中变量是通过百度地图可查，该式子求的是从任意风景区为起点游览完所有风景区并回到出发到原有的景区的最短路径；(3.2)和(3.3)是约束条件，目标函数(3.1)在(3.2)和(3.3)的限制每个旅游景区只能游览一次；对于每个风景区，只有风景区紧随其后的路线时，才会将它们之间的距离计入求和。而(3.5)是增加的约束变量，目的是为了避免子巡回。

假设存在子巡回，则至少有两个子巡回，那么至少有一个子巡回不包含起点城市1，例如 $p_{45}=1$ ，则

$v_4-v_5+n\le n-1$

$v_5-v_4+n\le n-1$

将两个不等式相加得到，这个结果错误，故不能存在子巡回。

对于整体巡回路线，只要 $v_i$ 取适当的值，都可以满足该约束条件：对于总巡回上的边， $p_{ij}=1$ ， $v_i$ 的大小取整数值，起点 $v=1$ ，第一个到达的城市，每到一个城市v加1，则必有 $v_i-v_j=1$ ，以上约束条件变成： $-1+n\le n-1$ ，显然成立。对于非总巡回上的边，以上约束条件变成： $-1\le n-1$ ，也显然成立。

3.4.2. 目标函数二：预算费用

$P_{总}={\displaystyle \underset{i=1}{\overset{3}{\sum }}{P}_i}$ (3.7)

$P_1={\displaystyle \underset{i,j\in scene}{\overset{n}{\sum }}PG\left(Qidia{n}_i,Zhongdia{n}_j\right)}$ (3.8)

$P_2={\displaystyle \underset{i,j}{\overset{n}{\sum }}{d}_{ij}\times P_n}$ (3.9)

$P_3={\displaystyle \underset{i\in scene}{\sum }PM+{\displaystyle \underset{j\in scene}{\sum }PL\times N{L}_{i,j}}}$ (3.10)

其中(3.8)针对通费用：即为旅游路线中，产生的乘坐的高铁中产生的费用总和。(3.9)针对燃油消耗费：即为每次旅游路线途中，在无法乘坐高铁的情况下，公交车在公路上行驶的总里程与各自单位里程的耗油费的乘积总和。(3.10)交针对游览费用：在游客游览过程中,游览景区的门票费用是必须考虑的，同时，游客在景区或城市逗留，而产生的住宿费用。

4. 蚂蚁算法解决TSP模型

4.1. 蚁群算法原理

论蚁群算法(Ant Colony Algorithm)是最近几年提出的一种新型的模拟进化算法，是一种寻找优化路径的概率型算法。该算法再求解TSP问题，分配问题等都取得了较好的结果。旅游景区的路线规划问题，可以认为是从一点出发，依次经过其他各点，且每个点仅经过一次，最后回到出发点的路线规划问题。即TSP回路问题。

现在我们建设基本的蚁群算法框架。假设现在我们有m个景区，n只蚂蚁。用表示景区于景区之间的距离。蚂蚁从一个城市前往下一个城市的依据有以下两点。

1) ${\alpha }_{ij}\left(t\right)$ 表示在t时刻，景区i到景区j间路径的信息强度。

2) ${\beta }_{ij}\left(t\right)$ 表示景区i和景区j的启发信息。一般情况下 ${\beta }_{ij}\left(t\right)=\frac{1}{d_{ij}}$ 。

3) $p_{ij}^s\left(t\right)$ 表示在t时刻，蚂蚁s由景区i转移至景区j的概率。

$p_{ij}^s\left(t\right)=\{\begin{array}{l}\frac{{\alpha }_{ij}^k\left(t\right){\beta }_{ij}^l\left(t\right)}{{\displaystyle \underset{r\in Tabl{e}_s}{\sum }{\alpha }_{ir}^k\left(t\right){\beta }_{ir}^l\left(t\right)}}j\in Tabl{e}_s\\ 0否则\end{array}$

其中 $Tabl{e}_s$ 为蚂蚁下一步进行的城市集合，随蚂蚁s的前行路程而改变。 ${\alpha }_{ij}\left(t\right)$ 的强度会随着时间而逐渐消逝，我们用p来表示消逝程度。

我们认为，蚂蚁选择前往的下一个城市会选择伪随机概率.因此，每当蚂蚁选择下一个城市时，我们就产生一个在[0, 1]区间内的一个随机数，然后根据这个随机数决定蚂蚁所前往的下一个城市。

$r=\{\begin{array}{l}\arg \max \left\{\left[\alpha \left(i,j\right)\right]{\left[\beta \left(i,j\right)\right]}^l\right\}若q\le q_0\\ R否则\end{array}$

其中q为区间[0, 1]内的随机数，为区间[0, 1]内的一个参数。

经过m次后，蚂蚁经过了所有城市，完成了一个循环。我们在根据公式对信息素进行更新

${\alpha }_{ij}\left(t+1\right)=\left(1-p\right)\cdot {\alpha }_{ij}\left(t\right)+\Delta {\alpha }_{ij}$

$\Delta {\alpha }_{ij}={\displaystyle \underset{k=1}{\overset{m}{\sum }}\Delta {\alpha }_{ij}^k}$

其中 $\Delta {\alpha }_{ij}$ 表示蚂蚁k在本次循环中在城市i于城市j之间的路径上增加的信息素。

$\Delta {\alpha }_{ij}^k=\{\begin{array}{l}\frac{Q}{L_k},如果蚂蚁k在t时刻到t+1时刻通过i,j\\ 0,否则\end{array}$

其中Q为常数， $L_k$ 为本次循环走过的路径长度。

4.2. 蚁群算法的实现步骤

1) $mc\leftarrow 0$ 各 ${\alpha }_{ij}$ 和 $\Delta {\alpha }_{ij}$ 的初始化；将n只蚂蚁至于m个点上。

2) 将各蚂蚁的初始出发点置于当前解集中；对于每只蚂蚁k，按概率 $p_{ij}^k$ 移至下一项点j，将顶点j置于当前解集。

3) 计算各蚂蚁的路径长度，记录当前的最好解。

4) 按更新方程修改轨迹强度。

5) 对各边弧 $\left(i,j\right)$ ，置 $\Delta {\tau }_{ij}\leftarrow 0$ ， $nc\leftarrow nc+1$ 。

6) 若小于预定的迭代次数且无退化行为，则转至步骤(2)。

7) 输出目前最好解。

程序运行结果与分析

先根据问卷调查结果确定费用与路程长对旅游影响的权重(3:7)，再通过蚁群算法求解在解决旅游最短路径问题主要首先构造一个解空间，最后基于信息素更新以及约束条件对解空间路径进行更新，并江苏省23个5A级景区数据按照蚁群算法原理得到结果如图1所示。

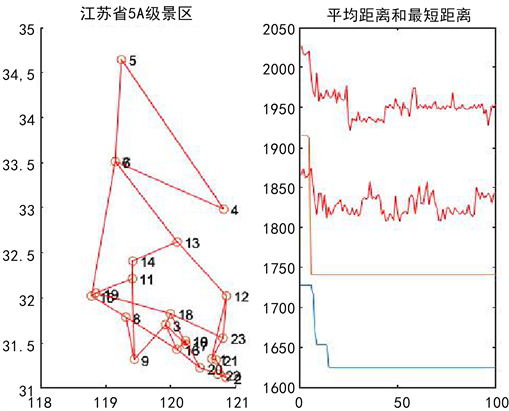
Figure 1. Operational results of ant colony algorithm

图1. 蚁群算法的运行结果

最短距离：1942千米。

最短路径：22 → 14 → 7→ 13 → 12 → 23 → 21 → 1→ 11 → 2 → 20 → 17 → 10 → 16 → 3 → 18 → 8 → 9 → 6 → 15 → 19 → 4 → 5。

从上述蚁群算法结果可以看出以最短路径为目标的旅游路线规划问题最佳路径为1942公里，通过此算法求解车费为745元，但是这里寻找到的最佳路径是局部最优解，而非全局最优解，所以需要对目前的蚁群算法进行改进。

4.3. 改进蚁群算法的求解步骤

蚁群算法利用正反馈原理和某种启发式算法的有机结合，容易出现早熟现象以及陷入局部的最优解.混合的思路是让妈蚁也具有“粒子”的特性 [3] ，首先蚂蚁按照蚁群算法，完成次遍历后，再让蚂蚁根据局部最优解和全局最优解进行调整。

调整思路如下：对于旅行商问题，其当前的位置是基本路径，让当前解与个体极值和全局极值分别作交叉操作。产生的解为新的位置，再作变异操作 [4] 。

改进后的算法解TSP问题的步骤如下：

1) 初始化：迭代步数nc设置为0，在从大量的路径中选择比较优的路径，在这些路径留下信息素。将m只蚂蚁置于n个顶点上。

2) 根据当前位置调节各个值。

3) 将各蚂蚁的初始出发点置于当前解集中；对每只蚂蚁 $k\left(k=1,2,\cdots ,m\right)$ ，按照概率移至下一顶点j；将顶点j置于当前解集。

4) 对每只蚂蚁进行交叉变异操作，找出全局极值和全局极值位置。

5) 计算各蚂蚁的路径长度；记录当前的最好解。

6) 按更新方程修改轨迹强度。

7) 对各边弧 $\left(i,j\right)$ ，置 $\Delta {\tau }_{ij}\leftarrow 0$ ， $nc\leftarrow nc+1$ 。

8) 若迭代步数小于预定的迭代次数且无退化行为(即找到的都是相同的解)，则转至步骤(2)。

9) 输出目前最好解。

4.3.1. 改进的蚁群算法的运行结果和分析

针对蚁群算法和粒子群混合编程求解算法，得到的结果如图2所示。

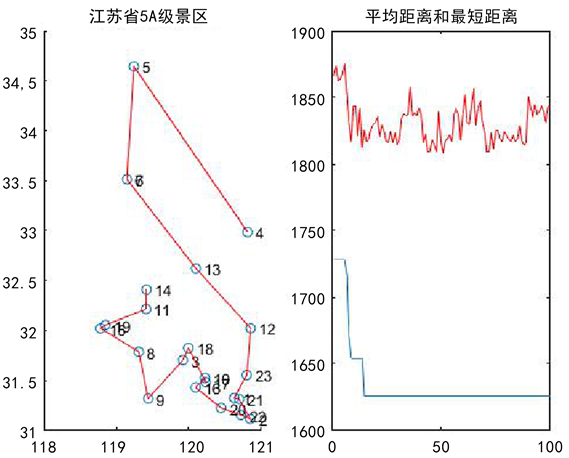
Figure 2. Running results of improved ant colony algorithm

图2. 改进后蚁群算法的运行结果

通过MATLAB编写的程序可得：

最短路程：1601千米；车费：570元。

最佳路径：

14 → 11 → 19 → 15 → 8 → 9 → 18 → 3 → 17 → 10 → 16 → 20 → 22 → 2 → 21 → 1 → 23 → 12 → 13 → 7 → 6 → 5 → 4。

所对应的景区分别是扬州瘦西湖风景区、镇江三山风景名胜区、南京钟山–中山陵风景名胜区、南京夫子庙–秦淮河风光带、镇江句容茅山景区、常州溧阳市天目湖景区、常州环球恐龙城景区、江苏省常州市中国春秋淹城旅游区、中央电视台无锡影视基地三国水浒城景区、无锡鼋头渚景区、无锡灵山大佛景区、吴中太湖旅游区、苏州吴江同里古镇景区、苏州周庄古镇景区、苏州市金鸡湖国家商务旅游示范区、苏州园林、苏州常熟沙家浜–虞山尚湖旅游区、南通市濠河风景区、泰州姜堰区溱湖国家湿地公园、大丰中华麋鹿园景区、淮安市周恩来故里景区、江苏省连云港花果山景区、江苏省徐州市云龙湖景区。

4.3.2. 模型总结

利用TSP模型对江苏省23个5A级景区做了一个初步的规划 [5] ，再通过蚁群算法对这些5A级景区进行路径选择，不仅大大节约运算的复杂性，而且高效的得出每两个景区的具体路线，为旅行爱好者提供便捷的服务。紧接着利用MATLAB编码结果可得的最短路径是1642千米，但是这个结果是局部最优而非全局最优。所以接下来就需要对蚁群算法进行改进，最后得到的路径是1601千米。车费为570元，门票费为2040元，住宿费2505元，总计费用为5115元。

5. 总结

通过基本的蚁群算法对TSP模型进行求解，提出了对蚁群算法进行改进。改进的主要目的是使得蚁群算法更好用于旅游规划问题，打破了基础蚁群算法只能控制局部最优解的局限，从而得到了全局最优解。MATLAB运行结果表明，改进的蚁群算法在最优路径求解和动态旅游路线规划方面都取得较好的效果。改进的模型特点有1、路径最短；2、每个景区只能浏览一次；3、无论城市规模大小都能得到理想的结论，而且求解的速度也相对较快；4、得出最短路径图，让不太熟悉地理位置的游客对景区有一个大致地了解。蚁群算法由于独立的特点，所以求解的稳定性较差 [6] ，即便是控制住参数，也可能得到不同的解，所以在求解时想要取得最优解不妨将主函数多运行几次。

基金项目

福建省大学生创新创业训练计划项目(项目编号：201811062076)。