输电线路树闪故障分析及树线距离预测方法研究

Research on Tree Flash Failure Analysis and Tree Line Distance Prediction Method for Transmission Line

摘要: 为应对线下超高树木引发的树闪故障，通过分析树闪故障隐患，确立树线距离预测的要素，在此基础上，根据树种类型及立地条件，建立树木生长模型，并依据输电线路应力变化以及温度等条件，建立导线弧垂变化模型。利用上述两个模型预测树线间距，提高电网运行的安全性。

Abstract: In order to cope with the tree flash failure caused by the ultra-high trees under the line, the tree line distance prediction factor is established by analyzing the hidden troubles of the tree flash fault. On this basis, the tree growth model is established according to tree type and site conditions, and the cable sag change model is established according to the stress change and temperature change of transmission line. The above two models are used to predict the spacing between tree lines and improve the safety of power grid operation.

1. 引言

随着电网建设规模的不断扩大，输电走廊穿越的地形愈加复杂，使得线路受树闪故障威胁的情况越来越多 [1] [2] [3] 。输电线路树闪故障发生的根本原因是输电线路与线下树木安全间距不足，电力线路两侧及下方的树木或者树木的一部分过度生长，使线路和树木之间的净空距离减小，当树枝与线路之间的距离小于必须的安全距离时，树闪故障就很有可能发生 [4] [5] 。同时，由于输电走廊穿越的地形复杂，线路运维人员很难及时准确地掌握走廊内树木生长情况。过去对树闪故障的预防往往集中在输电走廊树木的后期管理或者树木生长模型上，而实际情况中，导线弧垂变化对树线距离的影响同样不可忽视。因此，如果能够准确地预判树线间距，不仅可以提升输电线路的运行安全性，也能够有效节省线路运维人员的工作量。本文在分析输电线路树闪故障的基础上，建立树木生长模型以及导线弧垂变化模型，从而达到预测树线间距的目标，对输电线路运维工作具有指导意义。

2. 树闪故障分析

从故障发生的条件来看，树闪故障大致可分为3种情况 [1] ：

1) 在雨雪雷电等灾害天气情况下，输电走廊下方及周边的树木或断枝触碰电力线路，可能引发树闪故障甚至断线。对于灾害天气，电网有专门的应急机制，运维人员可以随时对故障情况做出反应并处理。

2) 在大风情况下，电力线路和树木都发生晃动，在晃动幅度较大使得树线安全间距不足时，线路就可能与电力走廊外的树木之间发生树闪故障。这种情况的树闪故障可能较多，但一般为瞬时性故障，自动重合闸一般能保证线路继续运行，不会造成重大的系统故障。

3) 在线路负荷较大的情况下，使得导线温度升高，从而使输电线路弧垂增加，尤其在夏季，不仅用电负荷会增大，也使导线散热减慢，线路弧垂增加幅度更大。这种情况下由树线安全间距不足引发树闪故障跳闸时，即使线路通过自动重合闸短时恢复运行也会由于导线过热下垂树闪而再度跳闸退出运行。当一条线路由于退出运行使得负荷转移到其它线路上时，容易使得其它线路过热而弧垂增加，造成连锁故障的发生。

基于以上分析，输电线路由于负荷增加引起的弧垂变化是引发大规模树闪故障的主要原因。因此，在进行树线距离预测时，除考虑树木生长因素外，还需计及线路负荷、应力变化等导致的弧垂变化。

3. 树线间距预测模型

3.1. 树木生长模型

树木生长模型构建

树木生长高度预测模型是在不同树种类型的基础上，考虑气象、土壤等立地条件，描述树高生长量随时间变化的规律，进而预测树木生长高度。

从模型构建原理的角度，可以将树木生长模型分为两大类，即理论模型和经验模型 [6] 。理论模型是借助数学方法演绎与推导所得，如Gompextz模型、指数回归模型、Smith模型等，经验模型则依赖于长期积累的经验数据，如Modified Weibull模型、二次抛物线模型等，不同模型适用条件与适用对象存在一定的差异。本文在Von Bertalanffy生长模型，即Richards生长方程的基础上进行优化，原Von Bertalanffy生长模型如下所示：

$\text{d}H/\text{d}t=K{\left(1-{\text{e}}^{-Am}\right)}^{A_1}$ (1)

其中 $\text{d}H/\text{d}t$ 代表树高生长量；K代表考虑了本地树木生长规律的树木生长速率的转化系数；m代表竞争因子，该值越大，则树木竞争力越强，越具有生命力；A、A₁表征不同种类树木的取值差异。

对上式进行积分，可以更加直观地得出树木生长高度Von Bertalanffy生长模型，如下所示：

$H=K{\left[1-{\text{e}}^{-m\left(t-t_0\right)}\right]}^n$ (2)

其中H代表在t时树木的高度；t₀为初始时间；m、n为常数，根据树种的不同其取值存在差异。其中K、m、n的参数求取见4.1。

3.2. 导线弧垂变化模型

输电线路弧垂增大是造成输电线路树闪故障的原因之一，弧垂的变化与导线温度及应力的变化有密切的关系。在悬挂点等高的情况下，应用架空线路状态方程 [7] ，得到：

${\sigma }_t^3+A{\sigma }_t^2+B=\text{0}$ (3-1)

$A=-\left[{\sigma }_0-\frac{E{\gamma }_0^2{l}^2}{24{\sigma }_0^2}-\alpha E\left({\displaystyle {\int }_{T_0}^T\frac{R{I}^2}{m{C}_p}\text{d}t}\right)\right]$ (3-2)

$B=\frac{E{\gamma }_t^2{L}^2}{24}$ (3-3)

其中 ${\sigma }_t$ 、 ${\sigma }_{\text{0}}$ 分别为所求以及初始状态下架空线弧垂点处的应力，MPa； ${\gamma }_t$ 、 ${\gamma }_{\text{0}}$ 分别为两种状态下架空的比载，MPa/m；T、T₀分别为导线的温度，℃；L为该档的档距，m；l为导线长度；α、E分别为架空线的温度膨胀系数和弹性模量；m为单位长度导线的质量，kg/m；C_p为导线综合热容系数，J/kg·℃；R分别为该段导线的电阻，Ω；I为流过导线的电流，A。

导线弧垂随应力变化情况如下：

$f=\frac{L^2{\gamma }_t}{8{\sigma }_t\cos \beta }$ (4)

联立(3)、(4)即可求得t时刻导线弧垂f。

3.3. 树线间距

在计及架空线路弧垂变化以及树木生长的条件下，树线垂直间距计算原理如图1所示。

结合前文计算得到的导线弧垂以及树木生长高度，即可求得在t时的树线间距：

$\Delta l=h-H-f$ (5)

4. 应用结果分析

4.1. 树木生长模型

由式(2)可知，建立的树木生长模型为非线性回归数学模型，其中K、m、n参数的求取过程如下：

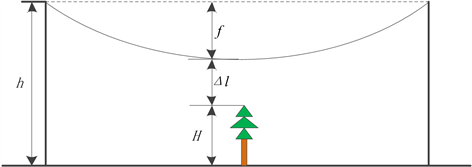
Figure 1. Tree line spacing calculation principle

图1. 树线间距计算原理

首先从当地林业部门获取不同树种不同时间的生长高度信息，以东北地区常见的沙松为例，在一定年限内其生长规律如表1所示。

Table 1. Tree growth height changes with time

表1. 沙松生长高度随时间变化规律

根据立地条件的差异，利用Excel软件绘制树高生长曲线，进一步拟合树高生长的回归方程：

$H=-a{x}^2+bx+c$ (6)

求得a = 0.1135，b = 4.279，c = −20.754。

选取不同的树龄t₁ = 9、t₂ = 12、t₃ = 15代入式(6)，可得树木生长高度H₁ = 8.65、H₂ = 11.81、H₃ = 14.57，进一步求取观测比：

$\lambda =\frac{\lg H_2-\lg H_1}{\lg H_3-\lg H_1}$ (7)

求得λ = 0.679。之后将H₁、H₂、H₃代入式(2)，联立式(4)进行规划求解，即可得到K、m、n各参数的值。

最终得到的沙松树木生长模型如下所示：

$H=20.752{\left(1-{\text{e}}^{-0.239t}\right)}^{10.325}$ (8)

4.2. 导线弧垂计算

以35 kV输电网中某段线路为例，杆塔水平档距L = 130 m，导线悬挂点距地面高度h = 20.75 m，导线型号为钢芯铝绞线，相关参数如表2所示。

线路的负荷情况不同时，导线的温度也有所不同。在不同导线温度下，通过导线弧垂变化模型求得的导线弧垂如表3所示。

Table 2. Wire parameter

表2. 导线参数

Table 3. Wire parameter

表3. 导线参数

4.3. 树线距离预测

在该线路下不同沙松初始高度的基础上，借助树木生长模型，计算未来其几年内生长的高度，并以导线弧垂计算结果中出现的最大值作为依据进行比较，得到树线间距，如表4所示。

Table 4. Tree line spacing prediction results

表4. 树线间距预测结果

按照相关规定要求 [8] ，各电压等级输电线路垂直方向上树线间距不应小于如下标准(表5)。

Table 5. Safety spacing of tree and wire

表5. 树木与导线安全间距

经比较可知，树木2在未来5年内与线路间距满足安全间距要求，可视为安全，树木2在3年后与树木的间距不足，视为存在树障隐患，应及时排除。

5. 结论

本文从树闪故障的分析出发，通过建立树木生长模型得到树木和导线弧垂变化模型，得到树木高度随时间变化的关系以及不同导线温度下导线的弧垂，预测树线间距，当树线安全间距小于标准规定时，则视为存在树障隐患并进行排除。

在输电线路后续的管理工作中，可在保持线路安全间距的前提下，根据树线预测间距的不同，确定树障隐患等级，并按照先后顺序处理树障隐患，在防止树闪故障发生的同时，也能减少线路运维人员的工作量。此外，由于地形和气象条件存在差异，树线距离预测结果会有一定的误差。在后续的工作中，随着更多实测数据的记录与分析，树木生长模型会更加完善，能够得到更加准确的树线距离预测结果，有效提高电力系统运行的安全性。

致谢

本文的研究离不开项目组人员的辛勤工作和专家提供的技术支持，特此向他们致以诚挚的感谢。

基金项目

国网吉林省电力有限公司科技项目2018-24号。