1. 引言
对接桁组件是运载火箭整流罩中的一个重要组成部分,其结构如图1所示。对接桁为“凸”字结构,底面铆接一块垫板用于保证对接桁的结构强度。对接桁通常为6米左右,其“A”面为对接装配面,平面度要求为0.5 mm,精度要求很高。对接桁组件的装配质量直接影响了运载火箭发射任务的成功。为此对接桁组件的铆接变形量要得到精确的控制,而铆接变形的分析就变得极其重要。
在以往的研究中,虽然有相关文献 [1] - [6] 对铆接变形过程进行过分析,但大多集中在单个铆钉、相同材料的铆接过程之中,而对于如图1示的铝制对接桁零件与钢垫板进行双面埋头铆接的过程还没有过相关研究,为此采用ANSYS/LS-DYNA软件对对接桁组件双面埋头铆接过程进行数值模拟有限元分析,从而得出不同铆接方式、不同铆接参数情况下对接桁组件的变形情况,为对接桁组件变形的控制提供理论依据,便于优化铆接工艺参数和过程。
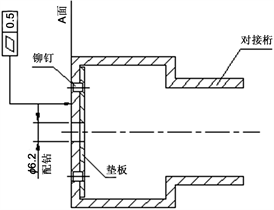
Figure 1. Diagram of assembly docking stringer
图1. 对接桁组件示意图
2. 对接桁组件铆接变形有限元分析过程及方案
2.1. 对接桁组件铆接变形模型的建立
对接桁组件双面埋头铆接有限元分析的物理模型如图2所示,其中铆接件1模拟对接桁零件,材料为2A12,厚度b1与对接桁一致为3 mm;铆接件2模拟垫板零件,材料为30CrMnSiA,厚度b2为1.5 mm,二者连接的铆钉材料为2A10,各种材料性能如表1所示。
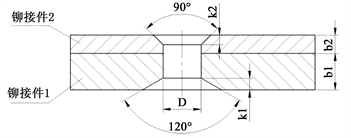
Figure 2. Finite element analysis model of docking riveting
图2. 对接桁铆接有限元分析物理模型

Table 1. Material properties of rivet and riveted parts
表1. 铆接与被铆接件材料性能
由于铆钉冲头与顶铁为淬火后镀铬的钢材,变形量可以忽略不计,故将其设置为刚性体。为模拟真实的铆接情况,本次仿真过程采用三维实体进行模拟分析,并采用六面体单元映射网格划分方法进行网格划分。采用此种划分方式是因为六面体单元计算精度高,不易产生退化单元,同时具有较好的计算效率,划分网格后的模型剖视如图3所示。格的单元类型选择为SOLID164,要原因是构建的实体结构较为简单,并且需要向接触表面加载法向压力,而该实体单元由8结点构成,可以通过其单元表面施加面载荷。各铆接件之间的接触采用面接触,摩擦系数一般设定为0.2。
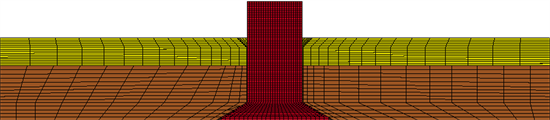
Figure 3. Finite element analysis mesh model for double-sided countersunk riveting
图3. 双面埋头铆接有限元分析模型网格图
在约束方面定义铆接件1和铆接件2四周均为无反射边界,而顶铁为固定约束。在施加载荷时,本次分析模拟锤击铆接与压铆铆接两种不同铆接方式下载荷,其中锤击铆接施加冲击载荷,按照铆接实际操作过程,以初速度为衡量标注设定载荷,根据铆钉长度L的不同给定冲头初速度分别为15 m/s、16 m/s、20 m/s,连续锤击5次;压铆铆接根据实际铆接过程施加匀速变压载荷,压铆时,给定冲头速度为0.25 m/s。
2.2. 铆接工况的划分
为分析出不同铆接方式及不同铆接参数下对接桁组件双面埋头铆接变形的情况,本研究中有限元分析共分18种工况,其中锤击铆接9种工况,伺服压铆9种工况,每种工况的区别为铆钉长度与划窝深度不同,具体如表2所示。

Table 2. Finite element deformation analysis of pressure riveting process
表2. 压铆变形过程有限元分析工况
3. 对接桁双面埋头铆接成形机理
采用有限元分析的方式对双面埋头铆接成形机理进行研究,有限元分析的基础参数以对接桁双面埋头压铆铆接过程为参考依据,经过分析,双面埋头铆接成形过程可分为如下四个阶段:
1) 初始阶段
初始阶段从压铆头移动开始到与铆钉钉杆接触为止,此阶段中铆钉未发生变形,铆钉钉杆处于即将受力的临界状态,初始阶段结束时如图4所示。
2) 钉杆镦粗阶段
此阶段从钉杆受力变形开始到钉杆镦粗胀满铆钉孔为止。由于铆钉杆与铆钉孔之间存在着0.05 mm的间隙,钉杆在刚开始受力时处于自由变形状态,即钉杆根据自身的力学性能形成中间粗两端细的“鼓形”镦粗结构;当钉杆逐渐镦粗,其最大外径会接触到铆钉孔壁,此时钉杆结束自由变形状态,其后钉杆的镦粗变形过程将受到铆钉孔的制约,铆钉孔会随着钉杆一起变形,但由于钉杆变形较快,会逐渐的将铆钉孔填满。最终当钉杆膨胀到一定程度后,钉杆与钉孔之间会达到挤压力的平衡状态,此时钉杆镦粗阶段结束。
如图5中可以看出,钉杆在变形过程中并不是对称的均匀的变形,由于压铆力直接作用在钉杆最下端,且是一次成形,就造成靠近铆钉头一侧的钉杆变形较小,在最根部位置更是几乎没有变化,如钉杆下端红色区域所示。由于这种现象,钉杆根部位置将会与钉孔产生间隙,但由于间隙很小,在实际铆接后可忽略不计,图6为钉杆根部位置放大25倍后情况。
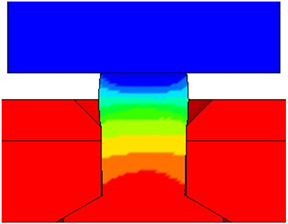
Figure 5. Status diagram of nail rod upsetting
图5. 钉杆镦粗阶段结束状态图

Figure 6. Enlarged picture of nail rod root’s interval
图6. 钉杆根部间隙放大图
3) 镦头成形阶段
镦头成形阶段开始后,钉杆与铆钉孔接触部分停止变形,而钉杆剩余部分则发生更大范围的塑性形变,并逐渐填满铆钉钉窝。当铆钉冲头与被连接件接触时,镦头成形阶段结束。
在镦头成形阶段,钉杆形成的镦头会对钉窝产生一定的压力,此压力垂直作用于钉窝表面,而钉窝部位钢板只有1.5 mm厚,刚性过小,故会造成钉窝位置凹陷,从而造成整个被连接件的翘曲现象。此种现象是造成双面埋头铆接变形的最直接因素,应采取措施减小其影响。在镦头成形阶段完成后,镦头与被连接材料之间的状态如图7所示,在镦头周围的局部范围内存在着凹陷,且镦头表面要略高于被连接件表面,此种现象产生的原因为,当铆钉冲头到达如图7所示的状态时,其与被连接件之间产生了接触,此时铆钉周围由于前述的原因已经产生了凹陷,但是对于铆钉冲头来说其作用的范围已经从铆钉钉杆变成了一个较大的平面,由于压铆过程较为平稳,压铆力会被均匀分布在冲头截面范围内的整个平面上,而不单独作用在铆钉上,故在如图7所示的位置,镦头表面与被连接件表面之间的高度差将不会发生变化,图8为铆接试片在25倍显微镜下的凹陷情况。
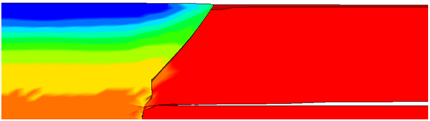
Figure 7. Partial picture of finite element of upsetting state
图7. 镦头成形阶段最终状态局部图

Figure 8. Practical picture of local upset head depression
图8. 镦头局部凹陷实物图
4) 压铆回弹阶段
压铆回弹阶段为整个双面埋头铆接的最终阶段,此阶段为铆接冲头达到压铆力从工件上回程的过程。在双面埋头铆接中,压铆机的设定参数为压铆力值,在一般情况下冲头在与被铆接件接触时,实际压铆力值会比设定值要小,故伺服压铆机会继续施加力直到达到设定值为止,而此时整个工件会因受力而产生弹性形变,在冲头回程的过程中,此形变会释放应力,从而达到平衡状态,此状态既为整个压铆过程的最终状态。如图9、图10所示,在回弹阶段铆接件有着明显的变形。
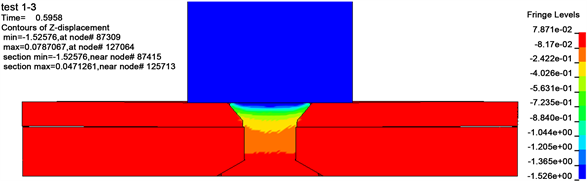
Figure 9. Spring-back stage of initial riveting state
图9. 压铆回弹阶段起始状态
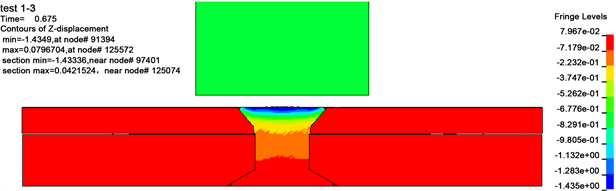
Figure 10. The final state of riveting rebound stage
图10. 压铆回弹阶段最终状态
4. 对接桁铆接变形有限元分析结果
4.1. 铆钉孔周围变形分析
铆钉孔周围的变形过程通过铆钉孔上参考点的位移变化来进行反应,参考点位置为均布在钉孔窝边沿上的参考点,最终得出了参考点的位移变化曲线示例如图11所示。
 工况1-1位移变化曲线
工况1-1位移变化曲线  工况2-1位移变化曲线
工况2-1位移变化曲线
Figure 11. Shifting displacement curve
图11. 工况位移变化曲线
通过分析认为在手工锤击铆接方式下,铆钉孔边缘位置参考点位移呈现周期性矩形波变化,而通过对比曲线高低点的位置与锤击铆接的时间,发现曲线变化的周期与锤击铆接的周期相同。此时铆钉孔周围的变形是随着锤击铆接的过程改变而改变的,当冲头与铆钉接触并释放冲击力时,铆钉孔周围会瞬间产生下陷;当冲击力释放完成,冲头回程并离开铆钉,铆钉孔周围产生回弹,直到下一次冲头冲击,如此反复。而由不同工况下伺服压铆铆接参考点位移变化图可以看出,铆钉孔边缘位置参考点随着压铆过程的进行,持续的产生下陷,并最终形成如图10所示的最终状态。
对比手工锤铆与伺服压铆两种铆接方式下的参考点位移曲线可以看出,在最终状态时,锤击铆接后铆钉孔周围各参考点尺寸分布在纵轴“0”点左右,范围大致在±0.02 mm之间,即铆钉孔周围呈现一种波浪起伏的变形状态,但由于变形较小,实物中很难发觉;而伺服压铆铆接后,各参考点的尺寸均在“0”点之下,均为负值,即铆钉孔周围呈现向中心凹陷的变形状态,且凹陷的程度随着压铆参数的改变而改变,此种情况与实际压铆情况相符。
4.2. 双面埋头铆接变形分析结果
在使用有限元分析的方式按不同工况模拟手工锤铆与伺服压铆过程后,将被铆接件单独进行变形分析,并采用位移变形云图的方式进行显示。由于在对接桁双面埋头铆接过程中,主要受力变形工件为钢垫板,而对接桁的整体变形是由钢垫板的变形引起,故此处只对钢垫板的变形情况进行分析。
如图12、图13所示为工况1-1、2-1情况下铆接过程的Z向(冲头运动的方向)位移云图。通过分析手工锤铆方式在不同工况下的钢板变形情况可以得出,在锤铆铆接情况下,钢板的变形没有规律可循,其变形后最高点出现的位置没有固定的区域,如云图12中红色区域所示;通过分析伺服压铆方式下不同工况的钢板变形情况,由变形云图可以看出,在压铆方式下钢板的变形较为规律,呈现一种由铆钉孔为中心“倒锥型”变化,最终形成中心凹陷、四周翘曲的形态,而钢板变形的最大位置均出现在钢板四周边角处。
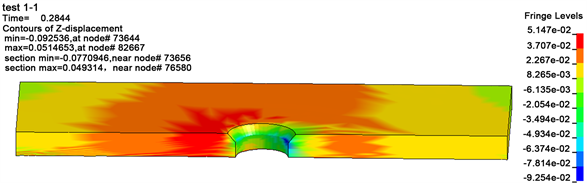
Figure 12. Z direction displacement curve cloud chart of status 1-1
图12. 工况1-1垫板Z向位移云图
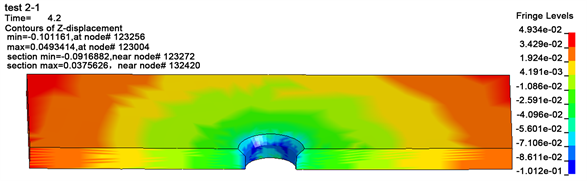
Figure 13. Z direction displacement curve cloud chart of status 2-1
图13. 工况2-1垫板Z向位移云图
通过分析不同工况下锤击铆接与压铆铆接的位移云图。可以看出,锤击铆接时,最大的应变节点发生在铆钉孔附近,Z向最大位移发生在铆接件2上下边缘处;压铆时,最大的应变节点发生在铆钉孔附近,Z向最大位移发生在铆接件2四周边缘,不同工况下的最大应变与Z向最大位移如表3所示。

Table 3. Maximum strain and Z-direction displacement of riveted parts 2 under different working conditions
表3. 不同工况条件下铆接件2的最大应变和Z向最大位移
5. 结束语
本文对对接桁组件双面埋头铆接过程进行有限元分析,从而得出不同铆接方式、不同铆钉长度和不同划窝深度情况下对接桁组件的变形情况:
1) 在相同工况下,对接桁压铆铆接的变形量要小于锤击铆接的变形量,且压铆铆接过程变形过程较为稳定;
2) 根据铆接变形有限元分析的结果,认为当铆钉长度L为6 mm、划窝深度k2为0.8 mm、铆接方式为伺服压铆时,此时铆接变形最小,最大的应变节点发生在铆钉孔附近,Z向最大位移发生在铆接件2四周边缘。
参考文献