1. 引言及主要结果
宽度是函数逼近论在现代发展中所形成的主要方向之一,也是国内外研究的热点之一,它与计算复杂性有着密切的联系 [1]。宽度问题的研究开始于1936年,A. N. Kolmogorov [2] 做了开创性的工作,并且首先计算出Sobolev函数类
到
上的Kolmogorov宽度的精确渐近阶。到1954年吗,S. R Stechkin [3] 研究了在
特殊情况下有限维空间的Kolmogorov n-宽度的精确渐近阶与线性n-宽度的精确渐近阶。再到1960年,V. M. Tikhomirov [4] 给出了
宽度的精确渐近阶,其后发表了许多关于宽度问题的论文,使得宽度这方面的探究活跃起来。此后两年,A. Pietsch [5] 和M. I. Stein [6] 研究了在一般情形下当
时Kolmogorov n-宽度的精确渐近阶与线性n-宽度的精确渐近阶,到1974年,Ismagilov [7] 研究了当
时的精确渐近阶估计,这样有关有限维空间在
条件下的经典n-宽度的精确渐近阶的估计已得到了非常优美的结果,关于经典n-宽度的其他结果可见参考文献 [8]。2018年,王桐心 [9] 等讨论了无穷维恒等算子的Kolmogorov n-宽度。本文主要讨论概率框架下恒等算子的线性n-宽度。首先,介绍线性n-宽度的定义。
定义1.1. 设W为赋范性线性空间
的一非空子集,
,称
为W在X中的线性n-宽度,其中
取遍X中的秩不超过n的所有线性算子。
定义1.2. 设B为W的全部开子集所生成的Borel域,在B上赋予概率测度
,即
为定义在B上的
-可加的非负函数,且有
,令
,则称
为W在X中的线性概率
-宽度,其中的
表示取遍B中所有测度不超过
的子集。
定义1.3. 设
为两个赋范线性空间,其范数分别为
与
,T是X到Y的有界线性算子。令
,
,称
,为算子T的线性n-宽度,
为算子T的线性
-宽度。
设
,令
,其中
可知
为
上的一个范数,且
为Banach空间,且当
时,
,而
,所以无穷维恒等算子是
的有界线性算子,而不是
到
的有界线性算子。对于
,令
,
。
可知
为
上的范数,且
为Banach空间,记
为
中的单位球。令
时,对
由Hȍlder不等式:
因此
。令
,定义无穷维恒等算子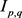 :
:
则
为
到
上的有界线性算子 [1]。
在下文中,令
,是和参数
有关的任意正常数。对两个正函数
和
,
,如果存在正常数
满足条件
,则记
。若存在正常数
满足条件
,则记
,若
且
,则记
。
本文利用离散化的方法讨论了概率框架下恒等算子的线性n-宽度,并得到其精确渐近阶。这就是本文的主要结果:
定理1:设
,
,
,且数列
满足
,
,
,则
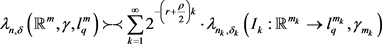
定理2:设
,则
2. 主要结果的证明
首先介绍有限维空间的线性
-宽度的相关结论。
令
。设
,
为
上的范数,
表示
按范数
所构成的Banach空间。记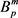 为
的单位球,则易知
为
的基,其中
。
为
的单位球,则易知
为
的基,其中
。
引理1 [8] :设
,则
定理1的证明:
首先建立离散化定理:对
,其中
,记
,则
,且
,有
,用
表示
中元素的个数,则
。
,有
这里
,且
为
的Schauder基。记
是由
构成的向量空间。
在
中赋予标准Guassiam测度
对
,记
,
为所对应特征向量,
,则:
记
。于是
。
定理1的上界估计:
对于
,
是
上的一个秩不大于
的线性算子,使得
存在映射:
。对于
,则存在一个线性映射
,满足
。显然: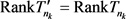 ,
。
,
。
考察集合
中子集
由Gaussian测度
和标准Gaussian测度
的定义可得
。
令
,则
,
,从而有:
定理1的下界估计:
对
,有
其中
。
设
,则有
即:
综上,定理1得证。
定理2的证明:
首先建立数列:
,
其中
且
,则
定理2的上界估计:
。
定理2的下界估计:
设
,则
,且
,于是
于是得到
综上,定理2得证。