1. 引言
换挡性能不仅能影响车辆的操作品质和性能,也是整车厂操控系统集成功能的重要指标。用户实践反馈表明汽车动态换挡性能是驾驶舒适性的重要指标之一 [1] 。
二次冲击是换挡过程中产生的第二个冲击,即第二个力峰值 [2] 。这是一种常见的动态换挡性能问题,越来越多的用户识别到此问题并开始抱怨。对此,国内一些高校或研究机构做了大量研究。刘荔斌等分析了二次冲击产生的机理,提出了非对称齿结构并通过试验验证了该改善策略的有效性 [3] ;运用ADAMS软件进行动态仿真,获得花键齿端最佳设计参数组合,从而降低二次冲击力峰值 [4] 。利用GSA系统进行换挡性能测试,通过改进变速箱换挡结构及相关参数,优化变速箱换挡性能 [5] ;以软轴式换挡操纵系统为研究对象,利用ANSYS有限元软件进行分析,得到应力和应变分布情况,对设计过程具有一定的参考价值 [6] 。为了改善同步器换挡锁止性能,研究还将同步器在性能试验台上对某变速器进行了换挡性能试验,测得换挡力、换挡位移、变速器输入和输出转速等试验数据,提高了综合性能 [7] ;研究还通过仿真的方法,运用UG和ADAMS建立同步器动态仿真虚拟样机,得到同步器主要参数对同步器换挡同步时间的影响主次关系,为研究换挡性能参数提供参考 [8] ;对某乘用车手动变速器动态换挡性能进行了主观评估及客观GSA测试,理论分析了二次冲击产生的原因,确定减小同步器齿厚和模数可减小变速器的二次冲击 [9] ;以某组合式动力换挡变速器手动变速模块为研究对象,通过Romax建立手动变速模块模型,对部分零部件进行仿真分析,研究了不同因素对变速器寿命的影响,对零部件设计参数及通用件和标准件选用合理性进行评价 [10] 。
为减少二次冲击带来的影响,对换挡外操作机构进行性能研究和结构优化。从NVH角度,在振动传递路径上,结合NASTRAN分析工具和相关的试验验证,找出影响换挡品质的因素,提出有效的改进措施。
2. 换挡机构分析
2.1. 换挡机构工作原理
换挡外操纵系统的三维模型如图1所示,包括变速杆、变速器基座、拉索总成、选换挡摇臂、变速器壳体及其附属部件。在进行选挡操作时,驾驶人左右移动变速杆,变速杆通过联动板的连接带动选挡拉索移动,完成选挡工作;接着进行换挡操作时,驾驶人前后移动变速杆,变速杆通过球头销的连接带动换挡拉索移动,完成换挡工作。
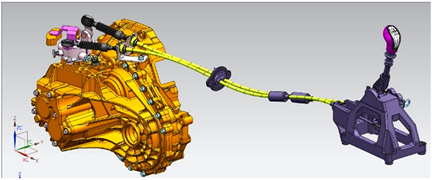
Figure 1. Shift out operating mechanism
图1. 换挡外操纵机构
2.2. 换挡机构模态
模态是结构的固有振动特性,模态参数是指固有频率、振型和阻尼比,不同结构的模态具有不同模态参数的表现形式,获取模态参数的计算或者试验分析的过程称之为模态分析 [11] 。
试验模态分析是通过试验测试采集系统输入与输出信号,运用数字信号处理技术拟合得到传递函数,再通过参数识别求出研究对象的模态参数 [12] 。
换挡机构是多自由度系统,其特征方程为:
(1)
式中,
为质量矩阵;
为阻尼矩阵;
为刚度矩阵;
为力向量;
为响应向量。
假定运动质点初位移和初速度为零,通过拉氏变换得到传递函数矩阵
(s为拉氏域变量):
(2)
式中,
为换挡机构的动刚度矩阵,
为换挡机构的输出位移拉氏变换,
为输入的拉氏变换。
在试验中,依次激励所有点,测量某一固定点的响应,即可得到传递函数矩阵,然后通过模态参数估计确定结构的固有频率、阻尼比和模态振型等。试验模态结果和数值计算模态相结合,不仅能为模态分析提供参考依据,为换挡机构最优化设计也能提供指导依据。
2.3. 换挡机构频响分析理论
频率响应函数(Frequency Response Function, FRF)为输入单位激励引起的输出位置的响应,包括位移、速度或加速度。在换挡机构的振动分析中,用简谐激励模拟二次冲击。
简谐激励下,弹簧质量系统的运动微分方程:
(3)
式中,m为质量块质量,c为粘性阻尼系数,k为弹簧刚度,x为位移响应量,
为简谐激振力。
简谐激振所引起的稳态强迫振动表达式为:
(4)
其中,B为振幅,
为激励频率,
为相位差。
工程上常用机械阻抗法来分析结构的动力特性。机械阻抗定义为简谐激振时复数形式的输入与输出之比。机械阻抗的导数称为频率响应函数,记为
。
(5)
式中,激振力
为输入项,位移
为输出项。
由频响函数可得到系统的幅频特性:
(6)
式中
为无阻尼弹簧质量系统的固有频率,
为相对阻尼系数。将
作为变量,以
为因变量画出的曲线
曲线称为系统的幅频特性曲线,它表示输出与输入的变化关系,如图2所示。当激振频率达到共振频率时,出现共振峰。
3. 有限元模型的建立
采用UG对变速器外操纵系统进行三维实体建模,利用Hypermesh提供的UG接口将模型导入。由于橡胶圈等一些细小的部件对分析影响较小,去掉此类部件,使模型简化,减少计算时间。由于选换挡拉索支架由薄板冲压而成,厚度在5 mm以下,因而可使用壳单元进行网格划分,换挡拉索护管接头、配重块、拉索护管接头等形状较规则的部件使用六面体进行划分,结构较为复杂的注塑件如拉索、拉索换挡杆等使用直接四面体进行划分。划分网格后的模型如图3所示,模型中共有91,067个节点,173,428个网格单元,其中2D单元401个。
划分网格后,赋予模型材料属性,包括材料的弹性模量E、泊松比NU、密度RHO等。此模型共使用了10种材料,材料的种类和相应的参数如表1所示。

Figure 3. Fem model of external control system
图3. 外操纵系统有限元模型图

Table 1. Material name and parameter list
表1. 材料名称及相应参数列表
对于模型的边界条件,RBE2是典型的刚性单元,用于模拟两个零件成为一体的情况,可用在没有相对运动的两个装配体之间的零件。本分析模型中,在配重块和拉索、拉索接头和拉索、拉索护管和选换挡支架之间等多处可添加RBE2单元。
模态分析与模型有效性验证
在仿真过程中,将已经建立好的外操纵系统有限元模型导入MSC.NASTRAN中,求解特征值。自由模态要求外操纵系统在自由状态下,即不受任何边界条件约束,分析频率设置为0至1000Hz,提交NASTRAN进行求解计算。仿真结果显示,其前六阶模态的值接近于0,为刚体模态,不是我们关注的重点。因此,从NASTRAN计算结果第7阶开始提取前9阶模态。
在模态试验中,采用力锤敲击来模拟激励,主要试验设备有BBM-PAK测试系统PCB-DEPEW.NY力锤、PCB-356A16加速度传感器和LMS Test. Lab分析软件。自由模态试验前,用刚度较小的弹性绳将整个外操纵系统吊在测试台上,保证变速器外操纵系统平稳,以最接近自由状态,忽略弹性绳的影响。模态试验采用多输入多输出(MIMO)法。本试验选择改变激励点的方法,选取10个激励点和3个响应点。如图4为测试点的选取位置。对比自由模态仿真结果与试验结果,如表2所示。

Figure 4. Select the location of the test points
图4. 测试点的选取位置

Table 2. Comparative analysis of free modal simulation and experimental results
表2. 自由模态仿真与试验结果对比分析
以上表格数据表明,仿真结果与试验结果的相对误差保持在10%以内,符合工程设计要求。有限元仿真获得的模态与试验结果总体比较吻合,验证了仿真模型的有效性。
4. 频率响应分析
在拉索接头处X轴方向加载单位载荷,频率范围为0 Hz~1000 Hz,如图5所示。分别观察换挡杆端部、换挡拉索配重块、换挡拉索支架处的响应,进行频率响应分析。
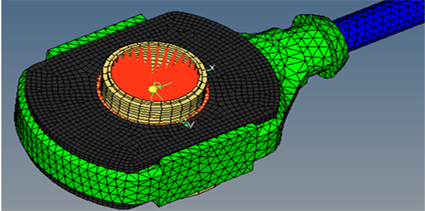
Figure 5. The position where dynamic loads are applied
图5. 施加动态载荷的位置
4.1. 系统阻尼系数对振动响应的影响
研究不同阻尼系数c下,换挡杆端部、配重块处、换挡拉索支架处的响应,如图6所示。将系统阻尼系数分别设定为0.01、0.03、0.06、0.09、0.12,观察共振频率处峰值的改变情况。
 (a)
(a)  (b)
(b) (c)
(c)
Figure 6. Response of corresponding position under different damping coefficients. (a) End of the rod; (b) Balancing weight; (c) Shift stay
图6. 不同阻尼系数下相应部位的响应。(a) 换挡杆端部;(b) 配重块;(c)换挡拉索支架处
换挡杆端部的响应如图6(a)所示,共振峰出现的频率分别是700 Hz和900 Hz,随着阻尼系数的增大,共振峰的幅值大幅降低,但阻尼系数增加到0.03后,幅值降幅不明显;配重块处的响应如图6(b)所示,共振峰出现的频率分别是260 Hz、420 Hz、620 Hz,随着阻尼系数的增大,共振峰的幅值大幅降低,但降幅逐渐减小;换挡拉索支架处的响应如图6(c)所示,共振峰出现的频率分别为420 Hz、620 Hz、920 Hz,随着阻尼系数的增大,共振峰的幅值大幅下降,但阻尼系数到0.03后,降幅不明显。
阻尼能有效抑制共振频率下的振动峰值,减小二次冲击造成的振动影响,同时减少振动沿外操作机构的传送,提高舒适感,降低噪声。在拉索支架安装座处添加橡胶垫,提高系统的阻尼系数,降低二次冲击峰值。但系统阻尼不是越大越好,增加到一定程度时,整个系统成刚性连接,反而起不到减振缓冲的效果。
4.2. 拉索支架刚度对振动响应的影响
研究不同拉索支架刚度下,换挡杆端部、配重块处、换挡拉索支架处的响应,如图7所示。将换挡拉索支架厚度T分别设定为8 mm、7 mm、6 mm、5 mm、4 mm,观察共振频率处峰值的改变情况。
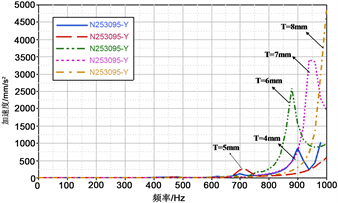
换挡杆端部的响应如图7(a)所示,随着拉索支架的厚度增加,刚度变大,共振峰向右移动,共振频率提高;低频段内,幅值有所降低,高频段内,幅值增大。配重块处的响应如图7(b)所示,随着拉索支架的厚度增加,刚度变大,共振峰向右移动,共振频率提高;低频段内,幅值有所降低,高频段内,幅值增大。换挡拉索支架处响应如图7(c)所示,随着刚度的增加,共振峰右移,共振频率提高。
 (a)
(a) 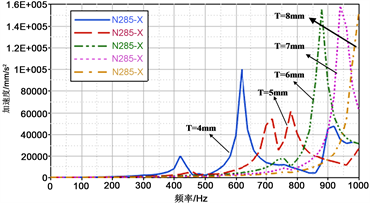 (b)
(b) 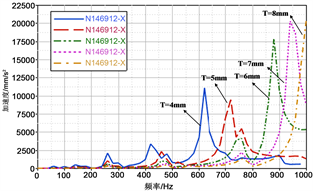 (c)
(c)
Figure 7. Response of the corresponding position under different stiffness of the cable supports. (a) End of the rod; (b) Balancing weight; (c) Shift stay
图7. 不同拉索支架刚度下相应部位的响应。(a) 换挡杆端部;(b) 配重块;(c)换挡拉索支架处
根据公式
,当质量m固定不变时,固有频率
与刚度k成正比关系。换挡拉索支架厚度T增大时,系统刚度k增大,各响应点的共振频率向右移动,即提高共振频率,避免产生共振,从而减小二次冲击,提高换挡舒适性;在低频段,随着厚度T的增大,二次冲击的峰值降低。增加拉索支架的厚度、改变拉索支架加强筋的结构等方法都可增加系统的刚度。但拉索支架厚度过大,将不利于整车的减重,应综合各因素选取合适的拉索支架厚度。
5. 结论
1) 在合适的范围内尽量增加整个系统的阻尼,有利于减小二次冲击的峰值。可考虑在拉索支架安装座处添加阻尼橡胶垫。
2) 增加换挡拉索支架的刚度,有利于减小产生的低频成分的二次冲击的峰值,同时提高产生共振的固有频率。可考虑适当增加拉索支架的厚度;改变拉索支架加强筋的结构,以增大刚度。
3) 适当减小换挡拉索接头刚度,有利于增大变形,吸收更多的二次冲击能量。可考虑对换挡拉索接头橡胶进行镂空设计。
致谢
感谢上汽通用五菱汽车股份有限公司CN200平台项目基金,感谢广西高校中青年教师科研基础项目(2019KY1550)。
NOTES
*通讯作者。