对称正定矩阵的分解

Decomposition of Symmetric Positive Definite Matrices

摘要: 基于对称正定矩阵的特殊性质，利用谱分解、拉格朗日插值、矩阵的交换性三种不同的思想将对称正定矩阵的分解进行延拓，并将其运用于解决更多的数学问题。

Abstract: Based on the special properties of symmetric positive definite matrix, the decomposition of symmetric positive definite matrix is extended by using three different ideas: spectral decomposi-tion, Lagrange interpolation and commutativity of matrix, and it is applied to solve more mathe-matical problems.

1. 引言

在高等代数中，对称正定矩阵是一类特殊矩阵。

设 $A\in R^{n\times n}$ ，若

$A=A^{\text{T}}$

对任意的

$0\ne X\in R^n$

都有

$X^{\text{T}}AX>0$

则称A为对称正定矩阵。

在具体应用中我们经常对其进行拆分使用。

实对称矩阵A正定当且仅当A与单位阵合同，即存在实可逆矩阵C，使

(1)

下面通过一个例子，简单说明，利用对称正定矩阵分解可证明相关矩阵的特征值的性质。

例 [1] ：设A，B都是n阶实对称矩阵，证明：

1) 若A正定或B正定，则AB的特征值全是实数；

2) 若A正定，则B正定的充要条件是AB的特征值全是正实数；

3) 若A，B都半正定，则AB的特征值都是非负实数。

这道题中，出现了正定矩阵以及与之相关的矩阵之间特征值的关系。事实上两个矩阵间的特征值的关联一般通过相似矩阵的特征值不变性建立的，所以这里需要考虑对对称正定矩阵A进行(*1)分解。

先考虑第一问，由于A为正定矩阵，必合同于单位矩阵 $E_n$。

由(1)，不妨设存在可逆矩阵C，使得

$A=C^{\prime }C$.

所以

. (2)

注意到 $C^{\prime },C$ 在B的同一侧，想要利用类似相似的结构则在 $C^{\prime }CB$ 两侧同时左乘 ${\left(C^{\prime }\right)}^{-1}$ 与右乘 $C^{\prime }$。得到

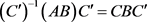. (3)

这说明，AB相似于 $CB{C}^{\prime }$。注意到仍为实对称阵，所以其特征值全为实数，所以AB的特征值也全是实数。

(2)与(3)用于与(1)类似的思想解决，唯一不同的是(3)中的半正定矩阵矩阵只能分解为两个实矩阵的乘积，但不能确保是可逆矩阵，但是对任意正实数t， $A+t{E}_n$ 是正定矩阵，所以利用多项式对t的连续性，则可以较容易得到结论。∎

受上例中矩阵分解的启发，我们先考虑对称正定矩阵是否能分解两个相同对称正定矩阵的乘积。更进一步，思考对称正定矩阵能否表示为某个对称正定矩阵的乘幂形式。

2. 命题的证明与推广

命题1：一个实对称正定阵可以分解为两个相同实对称正定矩阵的乘积。

证明：设A为正定矩阵，则由内积空间的理论存在正交矩阵T，使得

$T^{\prime }AT=\left(\begin{array}{cccc}{\lambda }_1& & & \\ & {\lambda }_2& & \\ & & \ddots & \\ & & & {\lambda }_n\end{array}\right)$

其中 ${\lambda }_i,i=1,\cdots ,n$ 是矩阵A的n个特征值。

由于A为正定矩阵，所以

${\lambda }_i>0,i=1,\cdots ,n$.

即：

$A=T\left(\begin{array}{cccc}{\lambda }_1& & & \\ & {\lambda }_2& & \\ & & \ddots & \\ & & & {\lambda }_n\end{array}\right)T^{\prime }=T\left(\begin{array}{cccc}\sqrt{{\lambda }_1}& & & \\ & \sqrt{{\lambda }_2}& & \\ & & \ddots & \\ & & & \sqrt{{\lambda }_n}\end{array}\right)T^{\prime }T\left(\begin{array}{cccc}\sqrt{{\lambda }_1}& & & \\ & \sqrt{{\lambda }_2}& & \\ & & \ddots & \\ & & & \sqrt{{\lambda }_n}\end{array}\right)T^{\prime }$ ,

取

$C=T\left(\begin{array}{cccc}\sqrt{{\lambda }_1}& & & \\ & \sqrt{{\lambda }_2}& & \\ & & \ddots & \\ & & & \sqrt{{\lambda }_n}\end{array}\right)T^{\prime }$

则，且C是一个对称正定矩阵。

下面我们将命题1进行推广。

命题2：设A是n阶正定实对称矩阵，则对任意的正整数 $k>1$ ，必存在唯一的n阶正定实对称矩阵B，使 $A=B^k$ ，这样的正定矩阵B称为正定阵A的k次方根，记为 $B=A^{\frac{1}{k}}$。

证明1 [2] ：利用谱分解思想

设V是有限维空间， $\phi$ 是V上的线性算子，当V是酉空间时， $\phi$ 为正规算子；当V是欧式空间时， $\phi$ 为自伴随算子。

${\lambda }_1,{\lambda }_2,\cdots ,{\lambda }_k$ 是 $\phi$ 的全体不同的特征值， $W_i$ 为 $\phi$ 属于 ${\lambda }_i$ 的特征子空间，则V是 $W_i\left(i=1,\cdots ,k\right)$ 的正交直和。

设 $E_i$ 是V到 $W_i$ 上的正交投影，则 $\phi$ 有下列分解式：

$\phi ={\lambda }_1{E}_1+{\lambda }_2{E}_2+\cdots +{\lambda }_m{E}_m$

由正交投影的性质

不难得到：

${\phi }^k={\lambda }_1^k{E}_1+{\lambda }_2^k{E}_2+\cdots +{\lambda }_m^k{E}_m$

鉴于 $\phi$ 和 ${\phi }^k$ 结构上极为相似并且巧妙地把特征值的幂次方和算子的幂次方结合起来，所以我们的第一种证法从谱分解入手证明。

我们可以将A看作欧氏空间R上正定自伴随算子 $\phi$ 在某一组标准正交基下的表示矩阵；设 ${\lambda }_i\left(i=1,2,3,\cdots ,m\right)$ 为 $\phi$ 全体不同的特征值， $W_i\left(i=1,2,3,\cdots ,m\right)$ 为 $\phi$ 属于 ${\lambda }_i$ 的特征子空间，则V为 $W_i\left(i=1,2,3,\cdots ,m\right)$ 的正交直和。

这时若设 $E_i$ 为V到 $W_i$ 上的正交投影，则 $\phi$ 有下列分解式：

$\phi ={\lambda }_1{E}_1+{\lambda }_2{E}_2+\cdots +{\lambda }_m{E}_m$

令

$d_i={\lambda }_i^{1/k}\left(i=1,2,3,\cdots ,m\right)$

则

$\psi =d_1{E}_1+d_2{E}_2+\cdots +d_m{E}_m$

适合且 $\psi$ 也为正交自伴随算子。

若存在 $\theta$ 为R上的正定自伴随算子

且

${\theta }^k=\phi$

令

$\theta =b_1{F}_1+b_2{F}_2+\cdots +b_r{F}_r$

为 $\theta$ 的谱分解式，其中 $F_i$ 为正交投影算子，且 $b_i$ 为正实数。

由

${\theta }^k=\phi$ ， $\phi ={\displaystyle {\sum }_{i=1}^r{b}_i^K{F}_i}$

故由 $b_i^K$ 为 $\phi$ 的特征值且 $b_i$ 互不相同，可以得到

$r=m$ ， $b_i=d_i$

这里允许差一个次序。 而 $E_i\left(R\right)$ ， $F_i\left(R\right)$ 都是 $\phi$ 关于特征值 ${\lambda }_i$ 的特征子空间，则

$F_i=E_i$ ， $\psi =\theta$ ∎

证明2：利用拉格朗日插值法的思想

在证明一般情形时，我们发现A与 $A^k$ 的关系最后转化到了特征值的幂次方，如果我们换一个角度看待 ${\lambda }_i^k$ ，我们可以将其看作是由

${\lambda }_i^k\left(i=1,\cdots ,m\right)$

唯一确定的多项式，所以我们借助Lagrange插值多项式分两步进行证明。

Step 1

设A为正定矩阵，则存在正交矩阵r，使得

$A=P\left(\begin{array}{cccc}{\lambda }_1& & & \\ & \ddots & & \\ & & \ddots & \\ & & & {\lambda }_n\end{array}\right)P^{\prime }$(*)

我们先给出一个命题 [3] ：设A为n阶正定阵， ${\lambda }_1,{\lambda }_2,\cdots ,{\lambda }_n$ 为A的所有特征值，则对任何满足(*)的正交矩阵P，恒有

$P\left(\begin{array}{cccc}{\lambda }_1^{\frac{1}{k}}& & & \\ & \ddots & & \\ & & \ddots & \\ & & & {\lambda }_n^{\frac{1}{k}}\end{array}\right)P^{\prime }=f(A)$

证明：简便起见，不妨设 ${\lambda }_1,{\lambda }_2,\cdots ,{\lambda }_s$ 为A的所有不同特征值，则 ${\lambda }_1^{\frac{1}{k}},{\lambda }_2^{\frac{1}{k}},\cdots ,{\lambda }_n^{\frac{1}{k}}$ 中有且仅有s个不同的特征值，且 ${\lambda }_i$ 与 ${\lambda }_i^{\frac{1}{k}}$ 重数也相同( $i=1,\cdots ,s$ )，做拉格朗日插值多项式：

则 $f\left(\lambda \right)$ 是 $s-1$ 次多项式，且 ${\lambda }_i^{\frac{1}{k}}=f\left({\lambda }_i\right)$ ；( $i=1,\cdots ,s$ )，故得：

$\left(\begin{array}{cccc}{\lambda }_1^{\frac{1}{k}}& & & \\ & \ddots & & \\ & & \ddots & \\ & & & {\lambda }_n^{\frac{1}{k}}\end{array}\right)=\left(\begin{array}{cccc}f\left({\lambda }_1\right)& & & \\ & \ddots & & \\ & & \ddots & \\ & & & f\left({\lambda }_n\right)\end{array}\right)=f\left(\left(\begin{array}{cccc}{\lambda }_1& & & \\ & \ddots & & \\ & & \ddots & \\ & & & {\lambda }_n\end{array}\right)\right)$

于是对任何满足(*)的正交阵P，恒有

$P\left(\begin{array}{cccc}{\lambda }_1^{\frac{1}{k}}& & & \\ & \ddots & & \\ & & \ddots & \\ & & & {\lambda }_n^{\frac{1}{k}}\end{array}\right)P^{\prime }=Pf\left(\left(\begin{array}{cccc}{\lambda }_1& & & \\ & \ddots & & \\ & & \ddots & \\ & & & {\lambda }_n\end{array}\right)\right)P^{\prime }=f\left(P\left(\begin{array}{cccc}{\lambda }_1& & & \\ & \ddots & & \\ & & \ddots & \\ & & & {\lambda }_n\end{array}\right)P^{\prime }\right)=f\left(A\right)$ ∎

Step 2

由和一般情况一致的方法，题目要求的正定阵的存在性是显然的。

下对唯一性进行证明。设B是满足 $B^k=A$ 的n阶正定阵，且 ${\mu }_1,\cdots ,{\mu }_n$ 是B的特征值，则 ${\mu }_1^k,\cdots ,{\mu }_n^k$ 就是 $B^k=A$ 的全部特征值，但假设 ${\lambda }_1,{\lambda }_2,\cdots ,{\lambda }_n$ 为A的所有特征值，故不妨设 ${\lambda }_i={\mu }_i^k$ ，于是 ${\lambda }_i^{\frac{1}{k}}={\mu }_i$ ( $i=1,\cdots ,n$ )。因为B正定，所以存在正交阵P，使成立

$B=P\left(\begin{array}{cccc}{\lambda }_1^{\frac{1}{k}}& & & \\ & \ddots & & \\ & & \ddots & \\ & & & {\lambda }_n^{\frac{1}{k}}\end{array}\right)P^{\prime }$

而由假设 $B^k=A$ ，故得到

应用Step 1，则有 $B=f\left(A\right)$ ，这就证明了，满足 $B^k=A$ 的任何正定阵B都等于 $f\left(A\right)$ ，所以B是唯一的。∎

证明3：利用矩阵的交换性

注意到了实对称矩阵的正交相似标准型优美的分块对角结构，尝试利用矩阵的交换性进行唯一性的证明。

不妨设 $A=B^k=C^k$ ，设A不同的特征值为，其重数分别为 $r_1,r_2,\cdots ,r_t$ ，则 ${\lambda }_1^{\frac{1}{k}},\cdots ,{\lambda }_t^{\frac{1}{k}}$ 为B，C的公共特征值，则存在正交矩阵 $P_1,P_2$ ，使得

${P^{\prime }}_{1}B{P}_1=\left(\begin{array}{cccc}{\lambda }_1^{\frac{1}{k}}{E}_{r_1}& & & \\ & \ddots & & \\ & & \ddots & \\ & & & {\lambda }_t^{\frac{1}{k}}{E}_{r_t}\end{array}\right)$ , ${P^{\prime }}_{2}C{P}_2=\left(\begin{array}{cccc}{\lambda }_1^{\frac{1}{k}}{E}_{r_1}& & & \\ & \ddots & & \\ & & \ddots & \\ & & & {\lambda }_t^{\frac{1}{k}}{E}_{r_t}\end{array}\right)$

又 $B^k=C^k$ ，且

$B^k=P_1\left(\begin{array}{cccc}{\lambda }_1{E}_{r_1}& & & \\ & \ddots & & \\ & & \ddots & \\ & & & {\lambda }_t{E}_{r_t}\end{array}\right){P^{\prime }}_1$ , $C^k=P_2\left(\begin{array}{cccc}{\lambda }_1{E}_{r_1}& & & \\ & \ddots & & \\ & & \ddots & \\ & & & {\lambda }_t{E}_{r_t}\end{array}\right){P^{\prime }}_2$

所以

${P^{\prime }}_2{P}_1\left(\begin{array}{cccc}{\lambda }_1{E}_{r_1}& & & \\ & \ddots & & \\ & & \ddots & \\ & & & {\lambda }_t{E}_{r_t}\end{array}\right)=\left(\begin{array}{cccc}{\lambda }_1{E}_{r_1}& & & \\ & \ddots & & \\ & & \ddots & \\ & & & {\lambda }_t{E}_{r_t}\end{array}\right){P^{\prime }}_2{P}_1$

即

$\left(\begin{array}{cccc}{\lambda }_1{E}_{r_1}& & & \\ & \ddots & & \\ & & \ddots & \\ & & & {\lambda }_t{E}_{r_t}\end{array}\right)$

可交换，所以 ${P^{\prime }}_2{P}_1$ 必为分块对角矩阵，则不妨设

${P^{\prime }}_2{P}_1=\left(\begin{array}{cccc}{B}_1& & & \\ & \ddots & & \\ & & \ddots & \\ & & & B_t\end{array}\right)$

$B_i$ 为分块对角矩阵， $i=1,2,\cdots ,t$ ，则 ${P^{\prime }}_2{P}_1$ 与分块对角矩阵 $\left(\begin{array}{cccc}{\lambda }_1^{\frac{1}{k}}{E}_{r_1}& & & \\ & \ddots & & \\ & & \ddots & \\ & & & {\lambda }_t^{\frac{1}{k}}{E}_{r_t}\end{array}\right)$ 也可交换。

即：

${P^{\prime }}_2{P}_1\left(\begin{array}{cccc}{\lambda }_1^{\frac{1}{k}}{E}_{r_1}& & & \\ & \ddots & & \\ & & \ddots & \\ & & & {\lambda }_t^{\frac{1}{k}}{E}_{r_t}\end{array}\right)=\left(\begin{array}{cccc}{\lambda }_1^{\frac{1}{k}}{E}_{r_1}& & & \\ & \ddots & & \\ & & \ddots & \\ & & & {\lambda }_t^{\frac{1}{k}}{E}_{r_t}\end{array}\right){P^{\prime }}_2{P}_1$

$P_1\left(\begin{array}{cccc}{\lambda }_1^{\frac{1}{k}}{E}_{r_1}& & & \\ & \ddots & & \\ & & \ddots & \\ & & & {\lambda }_t^{\frac{1}{k}}{E}_{r_t}\end{array}\right){P^{\prime }}_1=P_2\left(\begin{array}{cccc}{\lambda }_1^{\frac{1}{k}}{E}_{r_1}& & & \\ & \ddots & & \\ & & \ddots & \\ & & & {\lambda }_t^{\frac{1}{k}}{E}_{r_t}\end{array}\right){P^{\prime }}_2$

即 $B=C$。∎

3. 命题的应用

首先我们介绍求解线性方程组的Jacobi迭代法 [4] 。

设线性方程组

$Ax=b$

其中 $A\in M^{n\times n}$ ， $b\in I{R}^n$ ，A非奇异，且主对角元素 $a_{ii}$ 满足

$a_{ii}\ne 0,i=1,2,\cdots ,n$.

将A分解为

$A=D-L-U$

其中

$D=\left(\begin{array}{ccccc}{a}_{11}& & & & \\ & a_{22}& & & \\ & & \ddots & & \\ & & & a_{n-1n-1}& \\ & & & & a_{nn}\end{array}\right)$

$L=\left(\begin{array}{ccccc}0& & & & \\ -a_{21}& 0& & & \\ -a_{31}& -a_{32}& \ddots & & \\ ⋮& ⋮& ⋮& 0& \\ -a_{n1}& -a_{n2}& \cdots & -a_{n,n-1}& 0\end{array}\right)$

$U=\left(\begin{array}{ccccc}0& -a_{12}& -a_{13}& \cdots & -a_{21}\\ & 0& -a_{23}& \cdots & -a_{21}\\ & & 0& \cdots & ⋮\\ & & & \ddots & -a_{n-1,n}\\ & & & & 0\end{array}\right)$

则线性方程等价于

$DX=\left(L+U\right)X+b$

由假设可知 $D=diag\left(A\right)$ 非奇异。若记

$J=D^{-1}\left(L+U\right)$ , $f=D^{-1}b$

则可得

$x^{\left(k+1\right)}=J{x}^{\left(k\right)}+f,k=0,1,\cdots$

称之为Jacobi迭代格式，矩阵J称为Jacobi矩阵。

例1、设矩阵A对称正定

$D=diag\left(a_{11},a_{22},\cdots ,a_{nn}\right)$

试证明，若 $2D-A$ 正定，则Jacobi迭代法求解线性方程组

$AX=b$ (其中 $A\in M^{n\times n}$ ， $b\in I{R}^n$ )

必收敛。

证明：因为

又A为正定阵

$a_{ii}>0$

所以 $\forall x\ne 0$ ，有

$D^{-1/2}x\ne 0$

所以

${\left(D^{-1/2}x\right)}^{\text{T}}A\left(D^{-1/2}x\right)>0,x^{\text{T}}{\left(D^{-1/2}\right)}^{\text{T}}A{D}^{-1/2}x>0$

则 $D^{-1/2}A{D}^{-1/2}$ 为正定阵，所以 $E_n-D^{-1/2}A{D}^{-1/2}$ 特征值均小于1。

如果 $2D-A$ 也为正定矩阵，则 $D^{-1/2}\left(2D-A\right)D^{-1/2}$ 正定，即

$E_n-D^{-1/2}\left(2D-A\right)D^{-1/2}=-\left(E_n-D^{-1/2}A{D}^{-1/2}\right)$

特征值均小于1， $E_n-D^{-1/2}A{D}^{-1/2}$ 特征值均大于−1。因为J与 $E_n-D^{-1/2}A{D}^{-1/2}$ 相似，所以

$\left|\rho \left(J\right)\right|<1$

则线性方程组 $AX=b$ (其中 $A\in M^{n\times n}$ ， $b\in I{R}^n$ )必收敛。

事实上，在解决以上与对称正定阵有关的迭代法收敛证明问题中，采用了与常规应用正定阵性质，即 ${\alpha }^{\prime }A\alpha >0$ 不同的做法。其核心为将对角元大于零的对角矩阵D分解为 $D^{-1/2}{D}^{-1/2}$ 从而将J的特征值转化为 $E_n-D^{-1/2}A{D}^{-1/2}$ 的特征值，接下来论证 $E_n-D^{-1/2}A{D}^{-1/2}$ 的特征值即可。∎

例2、若存在对称正定矩阵P，使

$B=P-H^{\text{T}}PH$

为对称正定矩阵，试证明下列迭代格式收敛

$x^{\left(k+1\right)}=H{x}^{\left(k\right)}+b,k=0,1,\cdots$.

证明：

因为任意对称正定矩阵P可以拆分成两个相同对称正定矩阵的乘积，所以

$P=L^{1/2}{L}^{1/2}$ ,

得：

$\begin{array}{c}{L}^{-1/2}B{L}^{-1/2}=L^{-1/2}\left(P-H^{\text{T}}PH\right)L^{-1/2}\\ =E_n-L^{-1/2}{H}^{\text{T}}PH{L}^{-1/2}\\ =E_n-L^{-1/2}{H}^{\text{T}}{L}^{1/2}{L}^{1/2}H{L}^{-1/2}\end{array}$

因为B为对称正定矩阵，所以 $$ 正定。令

$C=L^{-1/2}{H}^{\text{T}}{L}^{1/2}$

则

$C^{\text{T}}={\left(L^{1/2}\right)}^{\text{T}}H{\left(L^{-1/2}\right)}^{\text{T}}$

因为 $L^{1/2}$ 为对称矩阵，则

$C^{\text{T}}=C$

则 $E_n-C{C}^{\text{T}}$ 的特征值均大于0，即C特征值的平方小于1，迭代格式收敛。∎

例3 [5] 、设A为实正规矩阵(即A满足 $A{A}^{\prime }=A^{\prime }A$ )，B也是实正规矩阵，P为非异阵，且 $B=P^{-1}AP$ ，证明：

${\left(P{P}^{\prime }\right)}^{\frac{1}{2}}A=A{\left(P{P}^{\prime }\right)}^{\frac{1}{2}}$.

证明：

首先我们注意到A和B相似，则它们的特征值也相同，且A，B均为实正规矩阵。由于实正规矩阵的特征值为正交相似关系的全系不变量，所以A，B正交相似。即∃正交矩阵 $P_1$ ，使得

${P^{\prime }}_{1}B{P}_1=A$.

由引理 [6] ：设V为n维欧式空间， $\phi$ 为V上的线性变换，则 $\phi$ 为正规算子的充要条件是存在某个实系数多项式 $g\left(x\right)$ ，使得

${\phi }^{*}=g(\phi )$

我们可以把矩阵B看作V上某正规算子 $\phi$ 在一组标准正交基下的矩阵，且在欧式空间中， ${\phi }^{*}$ 对应的表示矩阵就是 $B^{\prime }$。所以，存在实系数多项式 $f\left(x\right)$ ，使得 $B^{\prime }=f\left(B\right)$。自然猜想， $A^{\prime }$ 是否等于 $f\left(A\right)$。因为

$f\left(A\right)=f\left({P^{\prime }}_{1}B{P}_1\right)={P^{\prime }}_{1}f\left(B\right)P_1={P^{\prime }}_1{B}^{\prime }{P}_1={\left(P_{1}B{P^{\prime }}_1\right)}^{\prime }=A^{\prime }$

所以得到

$A^{\prime }=f\left(A\right)$.

又P为非异阵，所以 $P{P}^{\prime }$ 为正定矩阵， $\left(P{P^{\prime }}^{\frac{1}{2}}\right)$ 也为正定矩阵。

由命题的推广证法2中的步骤我们知道存在 $g\left(x\right)$ ，使得

$\left(P{P^{\prime }}^{\frac{1}{2}}\right)=g\left(P{P}^{\prime }\right)$

所要证明的式子变为

$g\left(P{P}^{\prime }\right)A=Ag\left(P{P}^{\prime }\right)$

则若能证明

$P{P}^{\prime }A=AP{P}^{\prime }$

那么

${\left(P{P}^{\prime }\right)}^{\frac{1}{2}}A=A{\left(P{P}^{\prime }\right)}^{\frac{1}{2}}$

于是我们继续分析：

要证

$P{P}^{\prime }A=AP{P}^{\prime }$

即证

$P{P}^{\prime }{A}^{\prime }=A^{\prime }P{P}^{\prime }$

即证

$P{P}^{\prime }f\left(A\right)=f\left(A\right)P{P}^{\prime }$

而：

$P^{-1}f\left(A\right)P=f\left(P^{-1}AP\right)=f\left(B\right)=B^{\prime }=P^{\prime }{A}^{\prime }{\left(P^{-1}\right)}^{\prime }=P^{\prime }f(A){\left(P^{-1}\right)}^{\prime }$

也就是

$P^{-1}f\left(A\right)P=P^{\prime }f\left(A\right){\left(P^{-1}\right)}^{\prime }$

即：

$P{P}^{\prime }f\left(A\right)=f\left(A\right)P{P}^{\prime }$

再由之前的讨论，题目得证。∎

4. 结语

对称正定矩阵的分解思想在许多领域有广泛的运用，本文受对称正定矩阵 $A=C^{\prime }C$ (其中C为实可逆阵)的启发，研究了更一般的分解 $A=CC$ 和它的推广 $A=C^k$ ，并给出了一些应用的例子，如在求解线性方程组的迭代法时，利用迭代矩阵的分解思想讨论迭代格式的敛散性等。希望我们能够在更多的数学领域中更好地应用对称正定矩阵分解的思想。

NOTES

^*并列第一作者。