1. 引言
车间调度是生产加工的关键环节,基本任务之一是合理安排各机器上的待加工工件的顺序,使得最大完工时间最短。轨道式导引小车(Rail-Guided Vehicle, RGV)由于其经济、容量大和灵活的特点,被广泛应用于车间调度 [1] [2] 。
现有的研究多采用启发式算法解决车间作业的调度问题,然而启发式算法容易陷入局部最优解的困境,不具有优良的全局寻优能力。本文在提出一种基于动态规划策略的RGV调度来解决直线往复式轨道装配调度问题,主要采用了分治算法的思想,将整体的大问题分而化之,成为若干个小问题,通过将小问题实现最优解以达到整体的优解 [3] [4] [5] 。
2. RGV调度问题描述
智能加工系统由M台计算机数控机床CNC、N道工序、1辆轨道式自动引导车RGV、1条RGV直线轨道、1条上料传送带、1条下料传送带等附属设备组成。不同的物料处理时间,移动时间,清洗时间均不同,同一物料不同工序的处理时间不同且不能用同一台CNC处理,RGV两边的CNC上下料时间也是不同的(具体如下图1),CNC在工作过程中有一定的概率发生故障,需要人工排除。已知各个步骤的相应时间,求一个比较好的动态调度模型。

Figure 1. Schematic diagram of intelligent machining system
图1. 智能加工系统示意图
2.1. 工序过程
1) 智能加工系统通电启动后,RGV在CNC1#和CNC2#正中间的初始位置,所有CNC都处于空闲状态。
2) 在工作正常情况下,如果某CNC处于空闲状态,则向RGV发出上料需求信号;否则,CNC处于加工作业状态,在加工作业完成即刻向RGV发出需求信号。
3) RGV在收到某CNC的需求信号后,它会自行确定该CNC的上下料作业次序,并依次按顺序为其上下料作业,若此时完成作业,已加工出熟料,则进行清洗作业。
4) RGV在完成一项作业任务后,立即判别执行下一个作业指令。此时,如果没有接到其他的作业指令,则RGV就在原地等待直到下一个作业指令。
某CNC完成一个物料的加工作业任务后,即刻向RGV发出需求信号。如果RGV没能即刻到达为其上下料,该CNC就会出现等待。
5) 系统周而复始地重复3)至4),直到系统停止作业,RGV回到初始位置。
3. 约束条件
3.1. 变量描述
首先假设调度队列为
,其中n表示需要加工的工件数。为了加工出最大的工件数,使机器效率最大化,我们应使n尽可能的大,即在一定的时间内RGV的调度时间尽可能的小 [6] [7] [8] 。
为了方便说明,在此对相关变量进行属性描述,设第i台机器的调度时间为l,RGV移动时间为m,上下料时间为t,清洗时间为
,离CNC工作结束还需
(包括物料工作或修理工作),物料需加工时间为
,物料已加工时间为
,此刻时间为T,上料开始时间为
,下料开始时间为
,故障开始时间为r,故障结束时间为
,人工修理时间为
,下一个物料上料开始时间为
,下一个物料的RGV移动时间为
,上下料时间为
,清洗时间为
。
接下来,设置两个决策变量:
1) 决策变量x
(1)
2) 决策变量y
(2)
3.2. 约束模型的建立
可建立约束模型如下:
(3)
根据上述约束,严格执行求得最优解。
4. 基于动态优先级算法的模型求解
4.1. 模型算法的建立
该模型算法,建立于多道工序,且需故障排除的情形下。在初始化时用一个数组记录各个步骤的相应时间,同时利用随机函数初始化故障开始时间,需要修理的时间,以及物料号,具体可以阐述为:在处理第i个物料时的t时刻起,机床CNC开始故障,需要人工修理时间为r。对于此类问题我们可以增设一个标志位,判断故障与否,当物料处理过程中发生故障,立刻停止处理,开始故障排除,排除故障后复位机床CNC状态位,以示RGV可以开始工作。在机器的工作时间下:
1.若CNC空闲
1-1若机器故障
a.物料数减1,不删除数据
1-2若CNC上无物料
a.更新上料开始时间,即总时间;
b.更新总时间:总时间+=上料开始时间;
c. CNC状态置位加工,有物料;
1-3若CNC有物料,则根据CNC物料工序道数:
a.更新总时间:总时间+=清洗时间;此时总时间即为下料开始时间;
b.更新此台CNC生产总时间:生产总时间+=需生产加工时间
c.若为最后一道工序,则生产物料总数加1
d.更新新物料上料开始时间,即总时间;
e.更新总时间:总时间+=需生产加工时间;
2.计算各CNC剩余加工时间
遍历CNC:
2-1若CNC故障
故障结束时间 = 故障开始时间 + 人工修理时间;
a.若总时间 < 故障结束时间
则剩余时间 = 故障结束时间 − 总时间;
b.否则,剩余时间 = 0,CNC状态复位;
2-2若CNC空闲,则剩余时间为0;
2-3若CNC工作
计算已加工时间:已加工时间 = 总时间 − 上料开始时间 − 上下料时间;
a.若已加工时间 < 生产加工时间
则剩余时间 = 需生产加工时间 − 已加工时间;
b.否则,剩余时间 = 0,CNC状态复位;
3.动态调度,计算最优选择
遍历CNC:
3-1若CNC无物料
a.若CNC正常
调度时间 = 路径时间 + 上料时间;
b.若CNC故障
调度时间 = 路径时间 + 上料时间 + 剩余加工时间;
3-2若CNC有物料
调度时间 = 路径时间 + 上料时间 + 清洗时间 + 剩余加工时间;
4.求出最短调度时间及索引位置;
5. RGV到索引位置等待,更新时间,若此时总时间大于机床故障开始时间,则置位该机床的故障标志位,回到步骤1;
该算法综合了就近原则、最短等待时间原则、最短上料时间原则,得出最短调度时间,通过此算法,可以得出较为良好的模型解。
4.2. 模型算法的验证
在进行验证说明前,为了方便,首先设置以下变量:在第n台机床CNC加工第i个物料的第j道工序的上料开始时间为
、上料结束时间为
、下料开始时间为
、下料结束时间为
、故障开始时间为
、故障结束时间为
、RGV移动时间长度为
,接下来,建立模型约束条件如下:
(4)
除了以上公式用于验证,还有逻辑衔接部分,即第n台机床CNC加工完成第i个物料的第j道工序时(同时上料),RGV移动至第
台机床CNC加工完成第i个物料的第
道工序(同时下料),此时若下料的物料已完成作业,则进行清洗熟料,然后开始在新的机床CNC开始加工第
块物料的第一道工序。在机床CNC进行这些操作步骤过程中,应该是连续衔接的。
5. 自适应遗传算法
为了对比分析本文算法的有效性,我们引入了自适应遗传算法。
自适应算法采用自适应的交叉变异参数,当个体差异大时,缩小差距,是优秀个体充分发挥,同时给次等个体一定机会进行进化。当个体差异大时,它则会扩大差距。自适应遗传算法在一定程度上缓解了陷入局部最优解的困境 [1] [9] 。
6. 实例分析
以2018年全国数学建模比赛为例,其中故障率为1%,故障排除时间介于10~20分钟之间,故障排除后即刻加入作业序列,其他基本数据如表1:
将算法转化为程序,经过MATLAB仿真可得出结果,如表2:
在8小时内,机器作业效率结果如表3:

Table 3. Results of operational efficiency (unit time: seconds)
表3. 作业效率结果(单位时间:秒)
根据表3可看到此题实例的部分结果,其中,在第一次加工物料9时,机床1在第470 s时发生故障,经人工修理了13分钟(1250 s)。经过验证,可知实例结果为正确无误的。通过表3可看出,此模型算法的作业效率。
为了验证本模型的良好性,采用了自适应遗传算法,通过多次循环求得局部最优解,得出了RGV运送物料以及CNC加工物料的顺序,为了方便说明,特意将第9块物料加工时设为故障,如表4。

Table 4. Optimal solution based on genetic algorithm
表4. 基于遗传算法最优解
为了更直观的说明,做出了甘特图以及两种算法对比图,如图2,图3。其中图3中,横坐标表示代码执行次数,纵坐标代表算法效率。可知自适应遗传算法所求局部最优解,往往需要多次执行算法以求得最优解。这不仅仅说明了本模型的解是最优解,具有良好性以及相对较高的作业效率,还说明了本算法的直接,简便。不需要多次执行就可以求得一个比较稳定的优解。

Figure 2. Gantt diagram of genetic algorithm
图2. 遗传算法甘特图
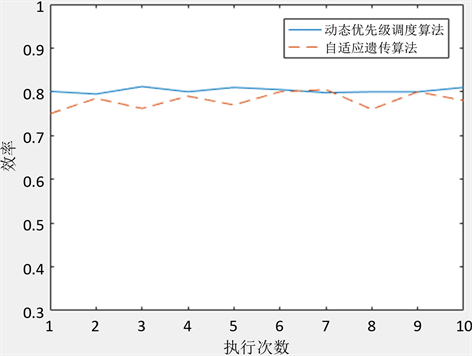
Figure 3. Efficiency comparison of the two algorithms
图3. 两种算法效率对比图
7. 模型的评价
7.1. 优点
1) 本文通过动态调度、分治算法的方式,使RGV在每执行完一个步骤之后,计算下一个最优步骤,可达到全局处于最优的状态,计算出最优调度模型,得到一个比较好的模型解。
2) 本模型考虑了多道工序的复杂情况,借鉴性强。
3) 本文所阐述的模型逻辑严谨,工序之间状况良好,具有较高的作业效率,且与实际关联密切,为实际生产提供了一个良好的可借鉴模型。
4) 本模型可用MATLAB软件加以验证,使我们的模型具有较高的可信度。
7.2. 缺点
1) 本模型参数与变量较多,算法较为繁琐。
2) 本模型算法偏向于暴力解决方式,对于大型工厂有较高的平台要求。