Allee效应对第一个种群具有避难所的偏害系统的动力学行为影响

The Influence of the Allee Effect on the Dynamic Behavior of Two Species Amensalism System with a Refuge for the First Species

摘要: 本文考虑了第一个种群内禀增长率具有Allee效应的第一个种群具有避难所的偏害系统，探讨了系统平衡点的存在性及其稳定性。研究表明：在考虑了第一个种群内禀增长率的Allee效应后，随着参数的变化，系统平衡点的个数和稳定性会发生变化，进而产生鞍结分支。

Abstract: In this paper, the Allee effect on the intrinsic growth rate is incorporate to the first species of two species amensalism model with a refuge for the first species. The existence and stability of the equilibria of the system are discussed. The study shows that after considering the Allee effect of the intrinsic growth rate of population, the number and the stability of equilibria of the system change with the change of the parameter and then the saddle-node bifurcation are generated.

1. 引言

偏利偏害是两个种群共存的一种生存模式。偏害是指在两个种群之间，一个种群会对另外一个种群产生不利的影响，但是这个种群却不会受到另一个种群的影响。近些年来，许多学者研究了偏害系统的动力学行为( [1] - [9] [13] )。

2016年，Xie，Chen和He在文 [4] 提出了对第一个种群加入避难所以保护其免受第二个种群的破坏的偏害系统：

$\{\begin{array}{l}\frac{\text{d}x}{\text{d}t}=a_{1}x\left(t\right)-b_1{x}^2\left(t\right)-c_1(1-k)x\left(t\right)y\left(t\right),\\ \frac{\text{d}y}{\text{d}t}=a_{2}x\left(t\right)-b_2{y}^2\left(t\right).\end{array}$ (1.1)

其中， $a_i,b_i,i=1,2,c_1,k$ 都是正常数。k是第一个种群的避难所，且 $0<k<1$。该系统存在三个边界平衡点

$E_0\left(0,0\right)$， $E_1\left(\frac{a_1}{b_1},0\right)$ 和 $E_2\left(0,\frac{a_2}{b_2}\right)$，系统还可能存在的平衡点是 $E_3\left(\frac{a_1{b}_2-a_2{c}_1\left(1-k\right)}{b_1{b}_2},\frac{a_2}{b_2}\right)$。作者探讨了这四个平衡点的稳定性， $E_0\left(0,0\right)$， $E_1\left(\frac{a_1}{b_1},0\right)$ 均不稳定，若 $0<k<1-\frac{a_1{b}_2}{a_2{c}_1}$，则 $E_2\left(0,\frac{a_2}{b_2}\right)$ 全局稳定；若 $1-\frac{a_1{b}_2}{a_2{c}_1}<k<1$，则 $E_3$ 是唯一全局稳定的正平衡点。这一结果表明对于两种群偏害系统，如果避难所的容量足够大，使得第一个种群受到第二个种群的影响是有限的，则两个种群能稳定共存。反之，如果避难

所非常小，则第一个种群仍然可能最终走向绝灭。

经典的Logistic系统：

$\frac{\text{d}N}{\text{d}t}=rN\left(1-\frac{N}{K}\right).$ (1.2)

(其中N是种群在t时刻的密度，r是内禀增长率，K是环境容纳量)只有唯一一个全局稳定的正平衡点 $N=K$，这个现象意味着种群能够长久生存下去。但是，随着人类对自然界的过度开发，越来越多的生物濒临灭绝，随着生物数量的减少，它们在择偶，抵御天敌，捕食等方面出现了极大的困难，所以，进一步降低了生物的出生率，这一现象在上个世纪30年代引起了学者Allee [18] 的关注。后来，学者们( [10] - [18] )先后建立并研究了各种各样描述这种现象的生物系统，我们称之为具有Allee效应的种群系统。

2005年，Zhou，Liu和Wang在文 [14] 中提出了食饵种群的内禀增长率具有Allee效应的捕食–食饵模型：

$\{\begin{array}{l}\frac{\text{d}N}{\text{d}t}=r_{1}N\left(\frac{N}{N+A_1}\right)-\epsilon PN,\\ \frac{\text{d}P}{\text{d}t}=-r_{2}P+\theta PN.\end{array}$ (1.3)

其中 $\frac{N}{N+A_1}$ 分别表示捕食者和食饵种群的Allee效应。作者的研究显示Allee效应可能会破坏捕食–食饵

系统的稳定性，系统的平衡点可能会从稳定变成不稳定，即使一个系统是稳定的，它也需要花更长的时间达到稳定状态。

2016年，刘志广，张丰盘和尤春晓在文 [16] 中提出了下面食饵种群具有弱Allee效应的捕食–食饵模型：

$\{\begin{array}{l}\frac{\text{d}N}{\text{d}t}=N\left(\frac{rN}{A+N}-aN\right)-bNP,\\ \frac{\text{d}P}{\text{d}t}=cNP-dP.\end{array}$ (1.4)

其中， $\frac{N}{A+N}$ 表示Allee效应。这里作者假设食饵种群的内禀增长率具有Allee效应。作者研讨了系统(1.4)

平衡点的局部稳定性，Allee效应会导致系统产生稳定的极限环，还会破坏共存平衡点的稳定性，使得原本简单的系统变得更加复杂，从而产生了超临界Hopf分支。

受文 [14] [16] 启发，注意到至今为止，尚未有学者探讨Allee效应对偏害种群模型的动力学行为影响，这启发我们在系统(1.1)的基础上提出如下第一种群内禀增长率具有Allee效应的偏害种群系统：

$\{\begin{array}{l}\stackrel{\dot{}}{x}=\frac{a_{1}x}{\beta +x}x-b_1{x}^2-c_1\left(1-k\right)xy,\\ \stackrel{\dot{}}{y}=a_{2}y-b_2{y}^2.\end{array}$ (1.5)

其中 $a_i\left(i=1,2\right),b_i\left(i=1,2\right)$ 分别表示第i个种群的自然增长率和密度制约即种内作用系数，k表示第一个种

群的避难所， $\frac{x}{\beta +x}$ 表示Allee效应， $\beta$ 表示Allee常数。 $a_i\left(i=1,2\right),b_i\left(i=1,2\right),c_1,\beta$ 都是正常数， $0<k<1$。显然，当 $x\to 0$ 时，有 $\frac{x}{\beta +x}\to 0$。也就是说种群数量很少时，种群的出生率也趋于0。而随着x的增大，当 $x\to \infty$ 时，有 $\frac{x}{\beta +x}\to 1$，也就是说随着种群数量的增加，Allee效应逐步减弱，最终当种群数量足够

大后，Allee效应就不会影响种群生长了。

我们将在下一节探讨中探讨系统(1.5)平衡点的存在性；第三节探讨(1.5)平衡点的稳定性；第四节探讨(1.5)的分支现象；第五节对(1.5)进行数值模拟加以验证。

2. 系统(1.5)平衡点的存在

定理2.1不论系统(1.5)的参数如何变化，系统(1.5)总存在两个边界平衡点： $E_0\left(0,0\right)$， $E_1\left(0,\frac{a_2}{b_2}\right)$。当 $a_1\ge b_1\beta$ 时，边界平衡点 $E_2\left(\frac{a_1}{b_1}-\beta ,0\right)$ 存在。系统(1.5)满足下列条件时可能存在正平衡点:

1) 当 $a_1<a^{\ast }$ 时，系统(1.5)没有正平衡点；

2) 当 $a_1=a^{\ast }$ 时，系统(1.5)只有唯一一个正平衡点 $E^{*}\left(x^{*},y^{*}\right)$ ；

3) 当 $a_1>a^{\ast }$ 时，系统(1.5)有两个正平衡点 $E_1^{*}\left(x_1^{*},y_1^{*}\right)$， $E_2^{*}\left(x_2^{*},y_2^{*}\right)$。

其中

$a^{*}=\frac{{\left(\sqrt{b_1{b}_2\beta }+\sqrt{a_2{c}_1(1-k)}\right)}^2}{b_2},$

$x^{*}=\sqrt{\frac{a_2{c}_1\beta \left(1-k\right)}{b_1{b}_2}},y^{*}=y_1^{*}=y_2^{*}=\frac{a_2}{b_2},$ (2.1)

$x_1^{*}=\frac{a_1{b}_2-b_1{b}_2\beta -a_2{c}_1\left(1-k\right)-\sqrt{{\left[b_1{b}_2\beta +a_2{c}_1\left(1-k\right)-a_1{b}_2\right]}^2-4a_2{b}_1{b}_2{c}_1\beta \left(1-k\right)}}{2b_1{b}_2},$ (2.2)

$x_2^{*}=\frac{a_1{b}_2-b_1{b}_2\beta -a_2{c}_1\left(1-k\right)+\sqrt{{\left[b_1{b}_2\beta +a_2{c}_1\left(1-k\right)-a_1{b}_2\right]}^2-4a_2{b}_1{b}_2{c}_1\beta \left(1-k\right)}}{2b_1{b}_2},$ (2.3)

$x_1^{*}<x^{*}<x_2^{*}.$

证明：系统(1.5)的正平衡点满足下面方程组

$\{\begin{array}{l}\frac{a_1{x}^2}{\beta +x}-b_1{x}^2-c_1\left(1-k\right)xy=0,\\ a_{2}y-b_2{y}^2=0.\end{array}$ (2.4)

由(2.4)的第二个方程可以解得 $y=\frac{a_2}{b_2}$，将其代入(2.4)的第一个方程中得到

$\frac{a_{1}x}{\beta +x}x-b_1{x}^2-c_1\left(1-k\right)\frac{a_2}{b_2}x=0.$ (2.5)

化简(2.5)得

$b_1{b}_2{x}^2+\left[b_1{b}_2\beta +a_2{c}_1\left(1-k\right)-a_1{b}_2\right]x+a_2{c}_1\beta \left(1-k\right)=0,$ (2.6)

(2.6)的判别式是

$\Delta ={\left[b_1{b}_2\beta +a_2{c}_1\left(1-k\right)-a_1{b}_2\right]}^2-4a_2{b}_1{b}_2{c}_1\beta \left(1-k\right)$。

为了后面讨论的方便，我们将(2.6)简记为

$A{x}^2+Bx+C=0.$ (2.7)

其中

$A=b_1{b}_2>0,B=b_1{b}_2\beta +a_2{c}_1\left(1-k\right)-a_1{b}_2,C=a_2{c}_1\beta \left(1-k\right)>0.$

下面分情况讨论：

1) 当 $\Delta <0$，此时通过计算得到 $a^{**}<a_1<a^{*}$，其中 $a^{**}=\frac{{\left(\sqrt{b_1{b}_2\beta }-\sqrt{a_2{c}_1\left(1-k\right)}\right)}^2}{b_2}$，

$a^{*}=\frac{{\left(\sqrt{b_1{b}_2\beta }+\sqrt{a_2{c}_1\left(1-k\right)}\right)}^2}{b_2}$。则(2.6)没有实数根，即系统(1.5)没有正平衡点。

2) 当 $\Delta =0$，此时 $a_1=a^{**}$ 或者 $a_1=a^{*}$，则(2.6)有唯一一个实数根 $x^{*}$。

a) 若 $a_1=a^{**}$，则(2.6)化为

${\left(\sqrt{b_1{b}_2}{x}^{*}+\sqrt{a_2{c}_1\beta \left(1-k\right)}\right)}^2=0,$

解得

$x^{*}=-\sqrt{\frac{a_2{c}_1\beta \left(1-k\right)}{b_1{b}_2}}<0.$

所以(2.6)没有正实数根，系统(1.5)没有正平衡点。

b) 若 $a_1=a^{*}$，(2.6)化为

${\left(\sqrt{b_1{b}_2}{x}^{*}-\sqrt{a_2{c}_1\beta \left(1-k\right)}\right)}^2=0,$

解得

$x^{*}=\sqrt{\frac{a_2{c}_1\beta \left(1-k\right)}{b_1{b}_2}}>0.$

所以(2.6)有唯一一个正实数根，系统(1.5)有唯一一个正平衡点 $E^{*}\left(x^{*},y^{*}\right)$，其中 $x^{*},y^{*}$ 见(2.1)。

3) 当 $\Delta >0$，计算得 $a>a^{*}$ 或者 $a<a^{**}$，此时(2.6)有两个不同的实数根 $x_1^{*},x_2^{*}$。

a) 若 $a>a^{*}$，此时 $B<0$，结合(2.7)，由韦达定理得到

$\begin{array}{l}{x}_1^{*}+x_2^{*}=-\frac{B}{A}>0,\\ x_1^{*}{x}_2^{*}=\frac{C}{A}>0.\end{array}$

所以可以得到 $x_1^{*}>0,x_2^{*}>0$。(2.6)有两个不同的正实数根，系统(1.5)有两个正平衡点 $E_1^{*}\left(x_1^{*},y_1^{*}\right)$， $E_2^{*}\left(x_2^{*},y_2^{*}\right)$，其中 $x_1^{*},x_2^{*},y_1^{*},y_2^{*}$ 见(2.2)，(2.3)，(2.1)。

由于下一节讨论正平衡点 $E^{*}\left(x^{*},y^{*}\right),E_1^{*}\left(x_1^{*},y_1^{*}\right),E_2^{*}\left(x_2^{*},y_2^{*}\right)$ 的局部稳定性会涉及到 $x_1^{*},x_2^{*},x^{*}$ 之间的大小关系，所以我们现比较它们的大小。

由(2.3)和 $a_1>a^{*}$ 通过适当的放大得到

$x_2^{*}>\frac{a_1{b}_2-b_1{b}_2\beta -a_2{c}_1\left(1-k\right)}{2b_1{b}_2}>\sqrt{\frac{a_2{c}_1\beta \left(1-k\right)}{b_1{b}_2}}=x^{*}.$

又由韦达定理

$x_1^{*}{x}_2^{*}=\frac{C}{A}=\frac{a_2{c}_1\beta \left(1-k\right)}{b_1{b}_2},$

因此

$x_1^{*}=\frac{a_2{c}_1\beta \left(1-k\right)}{b_1{b}_2}\frac{1}{x_2^{*}}<\sqrt{\frac{a_2{c}_1\beta \left(1-k\right)}{b_1{b}_2}}=x^{*}.$

所以 $x_1^{*}<x^{*}<x_2^{*}$。

b) 若 $a_1<a^{**}$，这时候 $B>0$，根据(2.6)和韦达定理

$\begin{array}{l}{x}_1^{*}+x_2^{*}=-\frac{B}{A}<0,\\ x_1^{*}{x}_2^{*}=\frac{C}{A}>0.\end{array}$

因此 $x_1^{*}<0,x_2^{*}<0$。所以(2.6)没有正实数根，系统(1.5)没有正平衡点。

综上所述得到定理2.1。

定理2.1得证。

3. 系统(1.5)平衡点的稳定性

系统(1.5)的雅克比矩阵为

$J\left(x,y\right)=\left(\begin{array}{cc}\frac{a_{1}x\left(x+2\beta \right)}{{\left(x+\beta \right)}^2}-2b_{1}x-c_1\left(1-k\right)y& -c_1\left(1-k\right)x\\ 0& a_2-2b_{2}y\end{array}\right)$。(3.1)

由(3.1)知系统(1.5)在 $E_0\left(0,0\right)$ 处的雅克比矩阵为 $J\left(E_0\right)=\left(\begin{array}{cc}0& 0\\ 0& a_2\end{array}\right)$，此时其两个特征值分别是 ${\lambda }_1=0$，

${\lambda }_2=a_2$。所以 $E_0$ 是非双曲的，不能直接判断其稳定性。接下来我们利用文 [19] 定理7.1来讨论其稳定性。

首先，我们在 $E_0$ 处作五阶幂级数展开得到

$\begin{array}{l}\frac{\text{d}x}{\text{d}t}=-c_1\left(1-k\right)xy+\left(\frac{a_1}{\beta }-b_1\right)x^2-\frac{a_1}{{\beta }^2}{x}^3+\frac{a_1}{{\beta }^3}{x}^4-\frac{a_1}{{\beta }^4}{x}^5+P_1\left(x,y\right),\\ \frac{\text{d}y}{\text{d}t}=a_{2}y-b_2{y}^2.\end{array}$ (3.2)

其中 $P_1\left(x,y\right)$ 是包含项 $x^i{y}^j\left(i+j\ge 6\right)$ 的幂级数。

然后，再作时间变换 $\text{d}\tau =a_2\text{d}t$ 得到

$\begin{array}{l}\frac{\text{d}x}{\text{d}\tau }=-\frac{c_1\left(1-k\right)}{a_2}xy+\frac{1}{a{}_2}\left(\frac{a_1}{\beta }-b_1\right)x^2-\frac{a_1}{a_2{\beta }^2}{x}^3+\frac{a_1}{a_2{\beta }^3}{x}^4-\frac{a_1}{a_2{\beta }^4}{x}^5+P_2\left(x,y\right),\\ \frac{\text{d}y}{\text{d}\tau }=y-\frac{b_2}{a_2}{y}^2.\end{array}$ (3.3)

其中 $P_2\left(x,y\right)$ 是包含项 $x^i{y}^j\left(i+j\ge 6\right)$ 的幂级数。

根据隐函数定理，在点 $\left(0,0\right)$ 的充分小领域内可由 $y-\frac{b_2}{a_2}{y}^2=0$ 解出 $y=\phi \left(x\right)=0$，从而得到

$\frac{\text{d}x}{\text{d}\tau }=\frac{1}{a_2}\left(\frac{a_1}{\beta }-b_1\right)x^2-\frac{a_1}{a_2{\beta }^2}{x}^3+\frac{a_1}{a_2{\beta }^3}{x}^4-\cdots .$ (3.4)

若 $\frac{a_1}{\beta }-b_1\ne 0$ 时，则 $m=2$， $a_m=\frac{1}{a_2}\left(\frac{a_1}{\beta }-b_1\right)\ne 0$。根据 [19] 定理7.1可知， $E_0\left(0,0\right)$ 是鞍结点。

若 $\frac{a_1}{\beta }-b_1=0$ 时，则 $m=3$， $a_m=-\frac{a_1}{a_2{\beta }^2}<0$。根据 [19] 定理7.1可知， $E_0\left(0,0\right)$ 是鞍点。

系统(1.5)在 $E_1\left(0,\frac{a_2}{b_2}\right)$ 处的雅克比矩阵为

$J\left(E_1\right)=\left(\begin{array}{cc}-c_1\left(1-k\right)\frac{a_2}{b_2}& 0\\ 0& -a_2\end{array}\right),$

此时，有两个特征值分别为 ${\lambda }_1=-c_1\left(1-k\right)\frac{a_2}{b_2}<0$， ${\lambda }_2=-a_2<0$，所以 $E_1$ 是稳定的结点。

若 $E_2$ 存在，则系统(1.5)在 $E_2$ 处的雅克比矩阵为

$J\left(E_2\right)=\left(\begin{array}{cc}-\frac{{\left(a_1-b_1\beta \right)}^2}{a_1}& -c_1\left(1-k\right)\left(\frac{a_1}{b_1}-\beta \right)\\ 0& a_2\end{array}\right),$

若 $a_1-b_1\beta >0$，则此时有两个特征值分别是 ${\lambda }_1=-\frac{{\left(a_1-b_1\beta \right)}^2}{a_1}<0$， ${\lambda }_2=a_2>0$，所以 $E_2$ 是鞍点。若 $a_1-b_1\beta =0$，则 $\frac{a_1}{b_1}-\beta =0$，此时 $E_2$ 与 $E_0$ 重合，所以 $E_2$ 仍然是鞍点。

下面我们探讨系统(1.5)正平衡点的稳定性。

系统(1.5)的雅克比矩阵为

$J\left(x,y\right)=\left(\begin{array}{cc}{F}_1& -c_1\left(1-k\right)x\\ 0& -a_2\end{array}\right),$

其中， $F_1=\frac{a_{1}x\left(x+2\beta \right)}{{\left(x+\beta \right)}^2}-2b_{1}x-c_1\left(1-k\right)y$。

则系统(1.5)在正平衡点处的特征值为 ${\lambda }_1=-a_2<0$， ${\lambda }_2=F_1$，所以正平衡点的稳定性是由 $F_1$ 决定的。

$\begin{array}{c}{F}_1=\frac{a_{1}x\left(x+2\beta \right)}{{\left(x+\beta \right)}^2}-2b_{1}x-c_1\left(1-k\right)y\\ =\frac{a_{1}x}{\beta +x}-b_{1}x-c_1\left(1-k\right)y+\frac{a_1\beta x}{{\left(\beta +x\right)}^2}-b_{1}x\\ =\frac{a_1\beta x}{{\left(\beta +x\right)}^2}-b_{1}x\\ =x\left[\frac{a_1\beta }{{\left(\beta +x\right)}^2}-b_1\right].\end{array}$

我们令 $g\left(x\right)=\frac{a_1\beta }{{\left(\beta +x\right)}^2}-b_1$，则正平衡点的稳定性由 $g\left(x\right)$ 决定。

因为 $g^{\prime }\left(x\right)=-\frac{2a_1\beta }{{\left(\beta +x\right)}^3}<0$，所以 $g\left(x\right)$ 在 $\left(0,+\infty \right)$ 上严格单调递减且 $g\left(\sqrt{\frac{a_1\beta }{b_1}}-\beta \right)=0$，下面比较 $x^{*}=\sqrt{\frac{a_2{c}_1\beta \left(1-k\right)}{b_1{b}_2}}$ 与 $\sqrt{\frac{a_1\beta }{b_1}}-\beta$ 的大小。

$\begin{array}{l}\left(\sqrt{\frac{a_1\beta }{b_1}}-\beta \right)-\sqrt{\frac{a_2{c}_1\beta \left(1-k\right)}{b_1{b}_2}}=\sqrt{\frac{a_1{b}_2\beta }{b_1{b}_2}}-\sqrt{\frac{b_1{b}_2{\beta }^2}{b_1{b}_2}}-\sqrt{\frac{a_2{c}_1\beta \left(1-k\right)}{b_1{b}_2}}\\ =\sqrt{\frac{b_1{b}_2{\beta }^2}{b_1{b}_2}+\frac{a_2{c}_1\beta \left(1-k\right)}{b_1{b}_2}+\frac{2\beta \sqrt{a_2{b}_1{b}_2{c}_1\beta \left(1-k\right)}}{b_1{b}_2}}-\sqrt{\frac{b_1{b}_2{\beta }^2}{b_1{b}_2}}-\sqrt{\frac{a_2{c}_1\beta \left(1-k\right)}{b_1{b}_2}}\\ =0.\end{array}$

所以 $x^{*}\text{=}\sqrt{\frac{a_1\beta }{b_1}}-\beta$，此时有 $g\left(x^{*}\right)=g\left(\sqrt{\frac{a_1\beta }{b_1}}-\beta \right)=0$。

因为 $x_1^{*}<x^{*}<x_2^{*}$，所以 $g\left(x_1^{*}\right)>g\left(x^{*}\right)=0$， $g\left(x_2^{*}\right)<g\left(x^{*}\right)=0$。

因此 $F_1\left(x_1^{*}\right)=x_1^{*}g\left(x_1^{*}\right)>0$， $F_1\left(x_2^{*}\right)=x_2^{*}g\left(x_2^{*}\right)<0$，所以 $E_1^{*}$ 是鞍点， $E_2^{*}$ 是稳定的结点。

而 $F_1\left(x^{*}\right)=x^{*}g\left(x^{*}\right)=0$，所以 $E^{*}$ 是非双曲的奇点，无法直接判断其稳定性。接下来我们利用文 [19] 中的定理7.1来判断其稳定性。

首先，我们先作变换 $X=x-x^{*}$， $Y=y-y^{*}$，将其平移到原点，并作五阶幂级数展开：

$\begin{array}{l}\frac{\text{d}X}{\text{d}t}=d_{01}Y+d_{02}{X}^2+d_{03}XY+d_{04}{X}^3+d_{05}{X}^4+d_{06}{X}^5+Q_1\left(X,Y\right),\\ \frac{\text{d}Y}{\text{d}t}=-a_{2}Y-b_2{Y}^2.\end{array}$ (3.5)

其中， $d_{01}=-c_1\left(1-k\right)x^{*}$， $d_{02}=\frac{a_1{\beta }^2}{{\left(\beta +x^{*}\right)}^3}-b_1$， $d_{03}=-c_1\left(1-k\right)$， $d_{04}=-\frac{a_1{\beta }^2}{{\left(\beta +x^{*}\right)}^4}$， $d_{05}=\frac{a_1{\beta }^2}{{\left(\beta +x^{*}\right)}^5}$， $d_{06}=-\frac{a_1{\beta }^2}{{\left(\beta +x^{*}\right)}^6}$。且 $Q_1\left(X,Y\right)$ 是包含项 $X^i{Y}^j\left(i+j\ge 6\right)$ 的幂级数。

接着，我们再作变换 $\left(\begin{array}{c}u\\ v\end{array}\right)=\left(\begin{array}{cc}1& \frac{d_{01}}{a_2}\\ 0& 1\end{array}\right)\left(\begin{array}{c}X\\ Y\end{array}\right)$ 得到：

$\begin{array}{l}\frac{\text{d}u}{\text{d}t}=d_{02}{\left(u-\frac{d_{01}}{a_2}v\right)}^2+d_{03}\left(u-\frac{d_{01}}{a_2}v\right)v-\frac{d_{01}{b}_2}{a_2}{v}^2+d_{04}{\left(u-\frac{d_{01}}{a_2}v\right)}^3\\ +d_{05}{\left(u-\frac{d_{01}}{a_2}v\right)}^4+d_{06}{\left(u-\frac{d_{01}}{a_2}v\right)}^5+Q_2\left(u,v\right),\\ \frac{\text{d}v}{\text{d}t}=-a_{2}v-b_2{v}^2.\end{array}$ (3.6)

其中 $Q_2\left(u,v\right)$ 是包含项 $u^i{v}^j\left(u+v\ge 6\right)$ 的幂级数。

最后，我们作时间变换 $\text{d}\tau =-a_2\text{d}t$ 得到：

$\begin{array}{l}\frac{\text{d}u}{\text{d}\tau }=-\frac{d_{02}}{a_2}{\left(u-\frac{d_{01}}{a_2}v\right)}^2-\frac{d_{03}}{a_2}\left(u-\frac{d_{01}}{a_2}v\right)v+\frac{d_{01}{b}_2}{a_2^2}{v}^2-\frac{d_{04}}{a_2}{\left(u-\frac{d_{01}}{a_2}v\right)}^3\\ -\frac{d_{05}}{a_2}{\left(u-\frac{d_{01}}{a_2}v\right)}^4-\frac{d_{06}}{a_2}{\left(u-\frac{d_{01}}{a_2}v\right)}^5+Q_3\left(u,v\right),\\ \frac{\text{d}v}{\text{d}\tau }=v+\frac{b_2}{a_2}{v}^2.\end{array}$ (3.7)

其中 $Q_3\left(u,v\right)$ 是包含项 $u^i{v}^j\left(u+v\ge 6\right)$ 的幂级数。

由 $v+\frac{b_2}{a_2}{v}^2=0$ 解得隐函数 $v=\phi \left(u\right)=0$，从而得到

$\frac{\text{d}u}{\text{d}\tau }=-\frac{d_{02}}{a_2}{u}^2-\frac{d_{04}}{a_2}{u}^3-\cdots ,$

因为 $m=2$， $a_m=-\frac{1}{a_2}\left[\frac{a_1{\beta }^2}{{\left(\beta +x^{*}\right)}^3}-b_1\right]\ne 0$，根据 [19] 定理7.1知， $E^{*}$ 是鞍结点。

定理3.1 当 $k<1-\frac{a_1{b}_2}{a_2{c}_1}$ 时， $E_1\left(0,\frac{a_2}{b_2}\right)$ 全局稳定。

证明：因为 $k<1-\frac{a_1{b}_2}{a_2{c}_1}$，所以 $a_1-c_1\left(1-k\right)\frac{a_2}{b_2}<0$，因此我们可以找到一个充分小的正数 $\epsilon >0$，使得 $a_1-c_1\left(1-k\right)\left(\frac{a_2}{b_2}-\epsilon \right)<0$。根据文 [20] 中的引理1.1.4知，对于上述的 $\epsilon$，存在一个正数 $T>0$，当 $t>T$ 时，有 $\left|y\left(t\right)-\frac{a_2}{b_2}\right|<\epsilon$ 成立，即 $\frac{a_2}{b_2}-\epsilon <y\left(t\right)<\frac{a_2}{b_2}+\epsilon$。

我们构造一个函数 $V\left(x,y\right)=x+y-y^{*}-y^{*}\ln \frac{y}{y^{*}}$，其中 $y^{*}=\frac{a_2}{b_2}$。 $V\left(x,y\right)$ 是一个正定函数。而 $V\left(x,y\right)$

沿着系统(1.5)的导数为

$\begin{array}{c}\stackrel{\dot{}}{V}=\stackrel{\dot{}}{x}+\left(y-y^{*}\right)\frac{\stackrel{\dot{}}{y}}{y}\\ =\frac{a_1{x}^2}{\beta +x}-b_1{x}^2-c_1\left(1-k\right)xy+\left(y-\frac{a_2}{b_2}\right)\left(a_2-b_{2}y\right)\\ =\left[\frac{a_{1}x}{\beta +x}-c_1\left(1-k\right)y\right]x-b_1{x}^2-\frac{1}{b_2}{\left(a_2-b_{2}y\right)}^2\\ \le \left[\frac{a_{1}x}{\beta +x}-c_1\left(1-k\right)\left(\frac{a_2}{b_2}-\epsilon \right)\right]x-b_1{x}^2-\frac{1}{b_2}{\left(a_2-b_{2}y\right)}^2\\ =\left\{\frac{\left[a_1-c_1\left(1-k\right)\left(\frac{a_2}{b_2}-\epsilon \right)\right]x-c_1\beta \left(1-k\right)\left(\frac{a_2}{b_2}-\epsilon \right)}{\beta +x}\right\}x-b_1{x}^2-\frac{1}{b_2}{\left(a_2-b_{2}y\right)}^2.\end{array}$

因为对所有的 $x>0$， $y>0$，都有 $\stackrel{\dot{}}{V}<0$， $\stackrel{\dot{}}{V}=0$ 当且仅当 $x=0$， $y=\frac{a_2}{b_2}$。因此 $\stackrel{\dot{}}{V}\left(x,y\right)$ 负定。所以 $E_1\left(0,\frac{a_2}{b_2}\right)$ 全局稳定。

4. 系统(1.5)的分支现象

在这一节中，我们将讨论系统(1.5)平衡点所出现的分支，前面定理2.1给出了正平衡点存在的充分条

件，观察可以得到当 $a_1>\frac{{\left(\sqrt{b_1{b}_2\beta }+\sqrt{a_2{c}_1\left(1-k\right)}\right)}^2}{b_2}$ 时，系统(1.5)有两个不同的正平衡点 $E_1^{*}\left(x_1^{*},y_1^{*}\right)$， $E_2^{*}\left(x_2^{*},y_2^{*}\right)$ ；当 $a_1=\frac{{\left(\sqrt{b_1{b}_2\beta }+\sqrt{a_2{c}_1\left(1-k\right)}\right)}^2}{b_2}$ 时，两个正平衡点重合为一个正平衡点 $E^{*}\left(x^{*},y^{*}\right)$ ；当 $a_1<\frac{{\left(\sqrt{b_1{b}_2\beta }+\sqrt{a_2{c}_1\left(1-k\right)}\right)}^2}{b_2}$ 时，系统(1.5)没有正平衡点。上述现象表明在正平衡点 $E^{*}\left(x^{*},y^{*}\right)$ 处可能存在一个鞍结分支。下面进行证明。

定理4.1系统参数满足临界条件

$a_1=a_{SN}=\frac{{\left(\sqrt{b_1{b}_2\beta }+\sqrt{a_2{c}_1\left(1-k\right)}\right)}^2}{b_2},$ (4.1)

时，系统(1.5)存在一个鞍结分支，此时 $a_1\equiv a_{SN}=\frac{{\left(\sqrt{b_1{b}_2\beta }+\sqrt{a_2{c}_1\left(1-k\right)}\right)}^2}{b_2}$，且 $a_1$ 作为分支参数。

证明：系统(1.5)在平衡点 $E^{*}\left(x^{*},y^{*}\right)$ 处的雅可比矩阵为

$J\left(E^{*},a_{SN}\right)=\left(\begin{array}{cc}0& -c_1\left(1-k\right)x^{*}\\ 0& -a_2\end{array}\right).$

因为 $\left|J\left(E^{*},a_{SN}\right)\right|=0$，所以 $J\left(E^{*},a_{SN}\right)$ 有一个零特征值，不妨记为 $\lambda$。

令V和W分别为矩阵 $J\left(E^{*},a_{SN}\right)$ 和 $J{\left(E^{*},a_{SN}\right)}^{\text{T}}$ 的属于特征值 $\lambda$ 的特征向量，计算得

$V=\left(\begin{array}{c}{V}_1\\ V_2\end{array}\right)=\left(\begin{array}{c}1\\ 0\end{array}\right),$ (4.2)

$W=\left(\begin{array}{c}{W}_1\\ W_2\end{array}\right)=\left(\begin{array}{c}1\\ -\frac{c_1\left(1-k\right)x^{*}}{a_2}\end{array}\right).$ (4.3)

而

$F_{a_1}\left(E^{*};a_{SN}\right)={\left(\begin{array}{c}\frac{x^2}{\beta +x}\\ 0\end{array}\right)}_{x=x^{*}}=\left(\begin{array}{c}\frac{x^{*2}}{\beta +x^{*}}\\ 0\end{array}\right),$ (4.4)

$\begin{array}{c}{D}^{2}F\left(E^{*};a_{SN}\right)\left(V,V\right)={\left(\begin{array}{c}\frac{{\partial }^2{F}_1}{\partial x^2}{V}_1^2+2\frac{{\partial }^2{F}_1}{\partial x\partial y}{V}_1{V}_2+\frac{{\partial }^2{F}_1}{\partial y^2}{V}_2^2\\ \frac{{\partial }^2{F}_2}{\partial x^2}{V}_1^2+2\frac{{\partial }^2{F}_2}{\partial x\partial y}{V}_1{V}_2+\frac{{\partial }^2{F}_2}{\partial y^2}{V}_2^2\end{array}\right)}_{\left(E^{*},a_{SN}\right)}\\ =\left(\begin{array}{c}\frac{2a_1{\beta }^2}{{\left(\beta +x^{*}\right)}^3}-2b_1\\ 0\end{array}\right).\end{array}$ (4.5)

所以

$W^{\text{T}}{F}_{a_1}\left(E^{*};a_{SN}\right)=\frac{x^{*2}}{\beta +x^{*}}\ne 0,$ (4.6)

$W^{\text{T}}\left[D^{2}F\left(E^{*};a_{SN}\right)\left(V,V\right)\right]=\frac{2a_1{\beta }^2}{{\left(\beta +x^{*}\right)}^3}-2b_1\ne 0.$ (4.7)

结合(4.6)和(4.7)，由 [21] 中的Sotomayor’s定理知系统(1.5)在 $E^{*}$ 处有一个鞍结分支。

定理4.1证明完毕。

5. 系统(1.5)数值模拟

1) a) 我们取值 $a_1=a_2=b_1=b_2=1$， $\beta =c_1=k=\frac{1}{2}$，此时 $\frac{a_1}{\beta }-b_1=1>0$，由前面分析知 $E_0\left(0,0\right)$ 是鞍结点， $E_1\left(0,1\right)$ 是稳定的结点， $E_2\left(\frac{1}{2},0\right)$ 是鞍点。图1所示。b) 取值 $a_1=a_2=b_1=b_2=\beta =1$， $c_1=k=\frac{1}{2}$，此时 $\frac{a_1}{\beta }-b_1=0$。则 $E_0\left(0,0\right)$ 是鞍点， $E_1\left(0,1\right)$ 是稳定的结点，此时 $E_2$ 与 $E_0$ 重合。图2所示。

Figure 1. Dynamics behaviors of the system (1.5), the parameters $\left(a_1,a_2,b_1,b_2,c_1,k,\beta \right)=\left(1,1,1,1,\frac{1}{2},\frac{1}{2},1\right)$

图1. 系统(1.5)的参数 $\left(a_1,a_2,b_1,b_2,c_1,k,\beta \right)=\left(1,1,1,1,\frac{1}{2},\frac{1}{2},1\right)$ 解的动力学行为

Figure 2. Dynamics behaviors of the system (1.5), the parameters $\left(a_1,a_2,b_1,b_2,c_1,k,\beta \right)=\left(1,1,1,1,\frac{1}{2},\frac{1}{2},\frac{1}{2}\right)$

图2. 系统(1.5)的参数 $\left(a_1,a_2,b_1,b_2,c_1,k,\beta \right)=\left(1,1,1,1,\frac{1}{2},\frac{1}{2},\frac{1}{2}\right)$ 解的动力学行为

2) a) 我们取值 $a_1=a_2=b_1=b_2=1$， $\beta =\frac{1}{4}$， $c_1=k=\frac{1}{2}$，此时 $\frac{{\left(\sqrt{b_1{b}_2\beta }+\sqrt{a_2{c}_1\left(1-k\right)}\right)}^2}{b_2}=1=a_1$，由定理2.1知，系统(1.5)只有唯一一个正平衡点 $E^{*}\left(\frac{1}{4},1\right)$，且该点是鞍结点。图3所示。b) 我们取值 $a_1=2$ , $a_2=b_1=b_2=1$， $\beta =\frac{1}{4}$， $c_1=k=\frac{1}{2}$，此时 $\frac{{\left(\sqrt{b_1{b}_2\beta }+\sqrt{a_2{c}_1\left(1-k\right)}\right)}^2}{b_2}=1<a_1=2$，由定理2.1知，系统(1.5)有两个正平衡点 $E_1^{*}\left(\frac{3-2\sqrt{2}}{4},1\right)$， $E_2^{*}\left(\frac{3+2\sqrt{2}}{4},1\right)$，其中 $E_1^{*}$ 是鞍点， $E_2^{*}$ 是稳定的结点。图4所示。

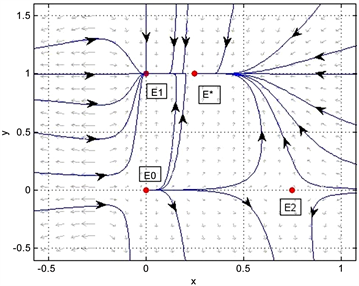
Figure 3. Dynamics behaviors of the system (1.5), the parameters $\left(a_1,a_2,b_1,b_2,c_1,k,\beta \right)=\left(1,1,1,1,\frac{1}{2},\frac{1}{2},\frac{1}{4}\right)$

图3. 系统(1.5)的参数 $\left(a_1,a_2,b_1,b_2,c_1,k,\beta \right)=\left(1,1,1,1,\frac{1}{2},\frac{1}{2},\frac{1}{4}\right)$ 解的动力学行为

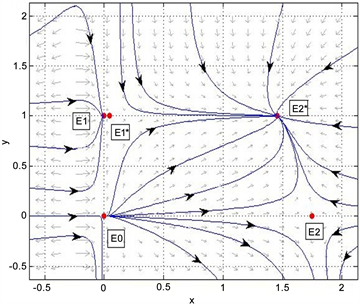
Figure 4. Dynamics behaviors of the system (1.5), the parameters $\left(a_1,a_2,b_1,b_2,c_1,k,\beta \right)=\left(2,1,1,1,\frac{1}{2},\frac{1}{2},\frac{1}{4}\right)$

图4. 系统(1.5)的参数 $\left(a_1,a_2,b_1,b_2,c_1,k,\beta \right)=\left(2,1,1,1,\frac{1}{2},\frac{1}{2},\frac{1}{4}\right)$ 解的动力学行为

3) 我们取值 $a_1=a_2=b_1=b_2=\beta =1$， $c_1=2$， $k=\frac{1}{4}$，此时有 $1-\frac{a_1{b}_2}{a_2{c}_1}=\frac{1}{2}>k=\frac{1}{4}$，由定理3.1知， $E_1\left(0,1\right)$ 全局稳定。图5所示，红黄蓝绿色线条分别取初值 $\left(2.8,1\right)$， $\left(0.5,0.7\right)$， $\left(1.3,2.5\right)$ 和 $\left(0.2,1.6\right)$。

Figure 5. $E_1$ is globally stable when the parameters $\left(\beta ,k\right)=\left(1,\frac{1}{4}\right)$ of the system (1.5)

图5. 系统(1.5)的参数 $\left(\beta ,k\right)=\left(1,\frac{1}{4}\right)$ 时 $E_1$ 的全局稳定

4) 我们取值 $a_1=a_2=b_1=b_2=1$， $c_1=2$， $k=\frac{1}{4}$，现在取一组固定初值 $\left(1.3,2.5\right)$，红蓝绿色线条分别取 $\beta =0.02,1.8,4.2$，则此时 $E_1\left(0,1\right)$ 是全局稳定，图6所示。我们发现Allee常数对系统(1.5)的第二个种群无明显影响。

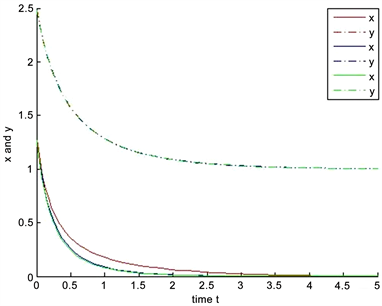
Figure 6. The influence of the parameters $\beta =\left(0.02,1.8,4.2\right)$ of the system (1.5) on the speed at solution tends to $\left(0,1\right)$

图6. 系统(1.5)的参数 $\beta =\left(0.02,1.8,4.2\right)$ 对解趋于 $\left(0,1\right)$ 速度的影响

6. 小结

Allee效应使得偏害系统的平衡点个数增加，并且平衡点的稳定性比较复杂(表1)：

Table 1. The existence and stability of the equilibrium point of the system (1.5)

表1. 系统(1.5)平衡点的存在性及其稳定性

7. 讨论

本文提出了第一个种群具有避难所，自然增长率具有Allee效应的两种群偏害系统。Xie，Chen和He在文 [4] 中探讨了第一个种群具有避难所的两种群偏害系统可能平衡点的局部稳定性和全局稳定性。通过对比，我们可以发现关于系统(1.5)的一些有趣的现象：

1) 系统(1.5)存在六个平衡点(包括三个边界平衡点和三个正平衡点)，而系统(1.1)只有四个平衡点(包括三个边界平衡点和一个正平衡点)。这是因为我们在第一个种群的内禀增长率上考虑了Allee效应，使得系统的平衡点个数增加。

2) 随着平衡点个数的增加，系统(1.5)的动力学行为变得更加复杂，例如：产生了鞍结分支。

3) 在第一个种群的内禀增长率上考虑了Allee效应，使得第一个种群满足一定条件下最终会趋于绝灭，并通过数值模拟发现在相同初值的情况下，随着Allee效应的增大，第一个种群绝灭的速度越快。说明了Allee效应不利于种群的生长，这是因为Allee效应会降低种群的出生率。

基金项目

福建省自然科学基金(No. 2017J01400)资助项目。