时变波动率模型下到期区间理财产品定价问题

Pricing of Financial Products in Maturity Interval under Time-Varying Volatility Model

摘要: 本文在时变波动率Black-Scholes模型下，研究了到期区间理财产品的定价问题。首先，利用偏微分方程方法得到了金融理财产品的定价公式。接着，利用二次变差方法提取积分波动率，再选取四种理财产品进行实证分析，并对其选择给出建议。最后，为投资者选择金融理财产品提供了一系列的参考建议。

Abstract: In this paper, we study the pricing of maturity interval financial products under the Black-Scholes model of time-varying volatility. First, the pricing formula of financial wealth management products is obtained by using the partial differential equation method. Then, the quadratic variation method is used to extract the integral volatility, and then four wealth management products are selected for empirical analysis, and suggestions are given for their selection. Finally, it provides a series of reference suggestions for investors to choose financial wealth management products.

1. 引言

随着时代的发展，我国个人财富以及个人理财有了较大增长。为了抵补资本在时间上的损失，人们常常将流动资产用于投资。同时，银行为了吸纳闲散资金，推出了各种理财产品，到期区间理财产品就是其中一种。

理财产品的核心问题是定价，一个理财产品是否成功，关键在于定价是否合理，是否能让发行单位和投资人实现双赢。金融理财产品的定价源自于欧式期权定价。目前，相关期权定价方法的理论研究日趋成熟。文献 [1] 以零息票为计价单位，研究了利率服从HJM模型下的欧式期权定价问题。为了刻画欧式期权价格估值的不确定性和投资者的犹豫程度，文献 [2] 用三角直觉模糊数表示风险资产的变化因子，构建了三角直觉模糊数的二叉树模型，进而研究了欧式期权定价问题。文献 [3] [4] 采用了摄动方法研究了非线性Black-Scholes模型下的欧式障碍期权定价问题。在一定的假设条件下，用Green函数分析了近似结论的误差估计。之后文献 [5] 采用单参数方法分别研究了修正的欧式期权定价问题，并且采用了Feymann-Kac公式分析了相应结论的误差问题。

关于期权定价方法的研究国内外有很多，但具体到银行理财产品定价问题的文献却不多见。考虑理财产品的价值是投资人选择理财产品的重要指标之一，同时，理财产品的定价对理财产品的投资活动具有指导意义。基于此，本文研究了挂钩于沪深300指数的到期区间理财产品定价问题。

2. 金融市场数学模型

表1收集了四款挂钩于沪深300指数的到期区间理财产品。在进行理财产品价值分析之前，先对沪深300指数适合的随机模型进行识别和参数估计。本节选取了2018年5月16日至8月14日的沪深300指数数据，时间间隔为1天，共计63个数据(见表2)。

Table 1. Agricultural bank of China financial services products

表1. 中国农业银行金融理财产品

Table 2. The csi 300 index data

表2. 沪深300指数数据

首先，将数据录入Eviews软件，取对数并一次差分后进行ADF检验，输出结果见表3，由结果可知t统计量为−8.333832，比三个临界值都要小，说明处理之后的数据不存在单位根，即通过单位根检验，故我们认定数据平稳。

Table 3. The csi 300 index opening price: the logarithmic difference the stationarity of data

表3. 沪深300指数开盘价格：对数差分数据的平稳性

其次，由数据的自相关性(见图1)，数据的自相关系数全部位于虚线内并且对应的P值均大于0.05，这表明数据之间不相关，符合白噪声序列的条件之一。

Figure 1. The csi 300 index opening price: logarithmic difference data correlation

图1. 沪深300指数开盘价格：对数差分数据的相关性

最后，由描述统计数据(见图2)，均值为−0.000204，中位数为−0.000641，最大值为0.034319，最小值为−0.038160，标准差为0.014282，偏度系数为0.035154，表明数据无偏，峰度系数为3.407955，表明数据的分布比标准正态分布略尖。计算得到的JB统计量的值为0.435568，对应的P值为0.804299，不能拒绝对数数据的一次差分是正态的。由表4也不能拒绝沪深300指数对数一次差分数据之间是独立的，从而我们可以认定沪深300指数对数一次差分为正态白噪声序列。

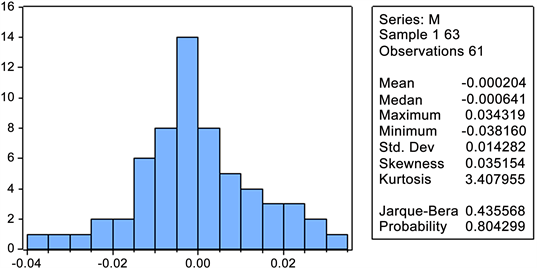
Figure 2. The csi 300 index opening price: statistical description of the log data of a difference

图2. 沪深300指数开盘价格：对数数据一次差分的统计描述

Table 4. The csi 300 index opening price: the independence of the log data of a difference

表4. 沪深300指数开盘价格：对数数据一次差分的独立性

基于以上分析，本文采用如下修正的几何Brown运动模型来描述进行对数一次差分处理后的沪深300指数

$\text{d}{S}_t=\mu \left(t\right)S_t\text{d}t+\sigma \left(t\right)S_t\text{d}{\omega }_t$ (1)

其中 ${\omega }_t$ 表示定义在完备概率空间 $\left(\Omega ,\mathcal{F},{\rm P}\right)$ 上的布朗运动，波动率 $\sigma \left(t\right)$ ，无风险收益率 $r\left(t\right)$ 和股票期望收益率 $\mu \left(t\right)$ 都是时间的函数。

在接下来的章节中，将用公式(1)刻画沪深300指数，并用其研究挂钩于沪深300指数的到期区间理财产品定价问题。

3. 区间金融理财产品的定价公式

根据到期区间理财产品的收益说明(见表1)，其到期之后的收益可以表示为

$\left(1+r_{1}T\right)I_{\left\{S\left(T\right)\in \left[K_1,K_2\right]\right\}}+\left(1+r_{2}T\right)I_{\left\{S\left(T\right)\notin \left[K_1,K_2\right]\right\}}$ (2)

其中 $S\left(T\right)$ 表示在到期日T时刻黄金的价格， $r_1$ 表示起始日的利率， $r_2$ 表示到期日的利率，[K₁, K₂]表示约定的执行区间。根据金融市场的自融资策略 [6] ，投入一个单位的本金、并且损益公式为公式(2)的金融理财产品的价格满足抛物偏微分方程。

$\{\begin{array}{l}LC=0,\left(t,S\right)\in \left(0,T\right]\times R_{+}\\ C\left(T,S\right)=\left(1+r_{1}T\right)I_{\left\{S\in \left[K_1,K_2\right]\right\}}+\left(1+r_{2}T\right)I{}_{\left\{S\notin \left[K_1,K_2\right]\right\}},S\in R_{+}\end{array}$ (3)

其中

$LC={\partial }_{t}C+\frac{1}{2}{\sigma }^2\left(t\right)S^2\left(t\right)S^2{\partial }_{ss}C+r\left(t\right)S{\partial }_{s}C-r\left(t\right)C$

下面我们考察公式(3)的解。令

$x=\ln S+{\displaystyle {\int }_t^{T}r\left(z\right)\text{d}z}-s,s=\frac{1}{2}{\displaystyle {\int }_t^T{\sigma }^2\left(s\right)\text{d}s}$ (4)

并定义

$C\left(t,S\right)=\exp \{-{\displaystyle {\int }_t^{T}r\left(z\right)\text{d}z}\}U\left(s,x\right)$ (5)

则

$\frac{\partial C}{\partial t}=\exp \{-{\displaystyle {\int }_t^{T}r\left(z\right)\text{d}z}\}\left[r\left(t\right)U-\frac{1}{2}{\sigma }^2\left(t\right)\frac{\partial U}{\partial s}+\left(-r\left(t\right)+\frac{1}{2}{\sigma }^2\left(t\right)\right)\frac{\partial U}{\partial x}\right]$

$\frac{\partial C}{\partial S}=\frac{1}{S}\exp \left\{-{\displaystyle {\int }_t^{T}r\left(z\right)\text{d}z}\right\}\frac{\partial U}{\partial x}$

$\frac{{\partial }^{2}C}{\partial S^2}=\frac{1}{S^2}\exp \left\{-{\displaystyle {\int }_t^{T}r\left(z\right)\text{d}z}\right\}\left[\frac{{\partial }^{2}U}{\partial x^2}-\frac{\partial U}{\partial x}\right]$

将上述结果代入公式(3)得

$\frac{\partial U}{\partial s}=\frac{{\partial }^{2}U}{\partial x^2},\left(s,x\right)\in \left[0,T\right]\times R$

由公式(4)和公式(5)可知，当 $t=T$ ， $U\left(0,x\right)=C\left(T,S\right)$ 时

$U\left(0,x\right)=\left(1+r_{1}T\right)I_{\left\{e^x\in \left[K_1,K_2\right]\right\}}+\left(1+r_{2}T\right)I_{\left\{e^x\notin \left[K_1,K_2\right]\right\}}$ (6)

根据热传导方程的经典解理论，其唯一强解可表示为

$U\left(s,x\right)=\frac{1}{2\sqrt{\pi s}}{\displaystyle {\int }_R{u}_0\left(z\right)\exp \left\{-\frac{{\left(z-x\right)}^2}{4s}\right\}\text{d}z}=I_1+I_2$ (7)

其中

$I_1=\left(1+r_{1}T\right)\frac{1}{2\sqrt{\pi s}}{\displaystyle {\int }_R{I}_{\left\{e^x\in \left[K_1,K_2\right]\right\}}\exp \left\{-\frac{{\left(z-x\right)}^2}{4s}\right\}\text{d}z}$

$I_2=\left(1+r_{2}T\right)\frac{1}{2\sqrt{\pi s}}{\displaystyle {\int }_R{I}_{\left\{e^x\notin \left[K_1,K_2\right]\right\}}\exp \left\{-\frac{{\left(z-x\right)}^2}{4s}\right\}\text{d}z}$

利用公式(7)可得本文的主要结论。

定理1 [7] 损益为公式(2)的金融理财产品在t时刻的价格为

$\begin{array}{c}C\left(t,S\right)=\left(1+r_{1}T\right)\exp \{-{\displaystyle {\int }_t^{T}r\left(z\right)\text{d}z}\}\Phi \left(d_1\right)-\left(1+r_{1}T\right)\exp \{-{\displaystyle {\int }_t^{T}r\left(z\right)\text{d}z}\}\Phi \left(d_2\right)\\ +\left(1+r_{2}T\right)\exp \{-{\displaystyle {\int }_t^{T}r\left(z\right)\text{d}z}\}\Phi \left(-d_1\right)+\left(1+r_{2}T\right)\exp \{-{\displaystyle {\int }_t^{T}r\left(z\right)\text{d}z}\}\Phi \left(d_2\right)\end{array}$ (8)

其中

$d_1=\frac{\ln S-\ln K_1+{\displaystyle {\int }_t^{T}r\left(z\right)\text{d}z}-\frac{1}{2}{\displaystyle {\int }_t^T{\sigma }^2\left(s\right)\text{d}s}}{\sqrt{{\displaystyle {\int }_t^T{\sigma }^2\left(s\right)\text{d}s}}}$

$d_2=\frac{\ln S-\ln K_2+{\displaystyle {\int }_t^{T}r\left(z\right)\text{d}z}-\frac{1}{2}{\displaystyle {\int }_t^T{\sigma }^2\left(s\right)\text{d}s}}{\sqrt{{\displaystyle {\int }_t^T{\sigma }^2\left(s\right)\text{d}s}}}$

证明：*首先计算 $I_1$ ，利用积分换元，我们有

$\begin{array}{c}{I}_1=\left(1+r_{1}T\right)\frac{1}{2\sqrt{\pi s}}{\displaystyle {\int }_{\ln K_1}^{\ln K_2}\exp \left\{-\frac{{\left(z-x\right)}^2}{4s}\right\}\text{d}z}\\ =\left(1+r_{1}T\right)\frac{1}{\sqrt{2\pi }}{\displaystyle {\int }_{\frac{\ln K_1-x}{\sqrt{2\pi }}}^{\frac{\ln K_2-x}{\sqrt{2\pi }}}\exp \left\{-\frac{y^2}{2}\right\}\text{d}y}\end{array}$

从而

$I_1=\left(1+r_{1}T\right)\Phi \left(\frac{x-\ln K_1}{\sqrt{2s}}\right)-\left(1+r_{1}T\right)\Phi \left(\frac{x-\ln K_2}{\sqrt{2s}}\right)$ (9)

同理

$I_2=\left(1+r_{2}T\right)\Phi \left(\frac{\ln K_1-x}{\sqrt{2s}}\right)+\left(1+r_{2}T\right)\Phi \left(\frac{x-\ln K_1}{\sqrt{2s}}\right)$ (10)

将公式(9)和公式(10)代入公式(7)，可得结论成立。*

证毕。

4. 实证分析

下面我们用文中所得的结论研究表1所述的几种人民币金融理财产品。由于金融理财产品需要投资者初始时刻就必须决定是否购买，且不允许转让。从而只需考虑这些金融理财产品在0时刻的价值，既 $t=0$。

另外，在使用公式(10)之前，也必须事先确定近期沪深300指数的波动率函数 $\sigma \left(t\right)$ 的分别在区间 $\left[0,90/365\right]$ 和 $\left[0,62/365\right]$ 上的积分值。这样一来，问题就转化成了积分波动率 ${\displaystyle {\int }_0^{90/365}{\sigma }^2\left(s\right)\text{d}s}$ 和 ${\displaystyle {\int }_0^{62/365}{\sigma }^2\left(s\right)\text{d}s}$ 的估计问

题。受开盘制度的限制(周末、节假日不开盘)，使得表(1)中相邻数据之间的时间间隔并不统一，下面构造一种新的积分波动率估计方法。

对公式(1)利用Ito公式 [8] ，易得

$\text{d}\ln S\left(t\right)=\left[r\left(t\right)-\frac{1}{2}{\sigma }^2\left(t\right)\right]\text{d}t+\sigma \left(t\right)\text{d}{\omega }_t$

对任意的固定时间T，假定在有限的时间区间[0, T]上有n + 1个观测值， $S\left(t_0\right),S\left(t_1\right),\cdots ,S\left(t_n\right)$ 其中 $0=t_0<t_1<\cdots <t_n=T$ 是区间[0, T]的任一分割。令 ${\Delta }_n=\underset{n}{\max }\left(t_i-t_{i-1}\right)$ ，则由二次变差过程的定义可知

$\left[\ln S,\ln S\right]\left(T\right)\stackrel{P}{=}\underset{{\Delta }_n\to 0}{\lim }{\displaystyle \underset{0<t_i\le T}{\sum }{\left(\ln S\left(t_i\right)-\ln S\left(t_{i-1}\right)\right)}^2}={\displaystyle {\int }_0^T{\sigma }^2\left(s\right)\text{d}s}$ (11)

这表明 ${\displaystyle \underset{0<t_i\le T}{\sum }{\left(\ln S\left(t_i\right)-\ln S\left(t_{i-1}\right)\right)}^2}$ 是积分波动率 ${\displaystyle {\int }_0^T{\sigma }_s^2\text{d}s}$ 的渐进无偏估计。此外，Banrndorff和Shepherd还证明了 ${\displaystyle \underset{0<t_i\le T}{\sum }{\left(\ln S\left(t_i\right)-\ln S\left(t_{i-1}\right)\right)}^2}$ 是积分波动率 ${\displaystyle {\int }_0^T{\sigma }_s^2\text{d}s}$ 的一致估计量 [9] [10] ，并且

$\frac{1}{\sqrt{{\Delta }_n}}{\left[{\displaystyle \underset{0<t_i\le T}{\sum }{\left(\ln S\left(t_i\right)-\ln S\left(t_{i-1}\right)\right)}^2-{\displaystyle {\int }_0^T{\sigma }_s^2\text{d}s}}\right]}^2\stackrel{P}{\to }N\left(0,{\displaystyle {\int }_0^T{\sigma }^4\left(s\right)\text{d}s}\right)$ (12)

其中 $\stackrel{P}{\to }$ 表示依概率收敛。至此，我们可以采用 ${\displaystyle \underset{0<t_i\le T}{\sum }{\left(\ln S\left(t_i\right)-\ln S\left(t_{i-1}\right)\right)}^2}$ 来估计积分波动率 ${\displaystyle {\int }_0^T{\sigma }^2\left(s\right)\text{d}s}$ ，

数据处理过程见表5，其中 $\ln s_i$ 是表1中沪深300指数的对数数据， $i=1,2,\cdots ,63$。

$x_j=\ln S_{j+1}-\ln S_j,j=1,2,\cdots ,62$

Table 5. The extraction of the csi 300 index integral volatility

表5. 沪深300指数积分波动率的提取

注意表1所列数据时间起点为2016年5月16日，终点为2016年8月12日，恰好90天，从而依据

公式(11)和(12)，可得90天的积分波动率 ${\displaystyle {\int }_0^{90/365}{\sigma }_s^2\text{d}s}$ 估计

${\displaystyle {\int }_0^{90/365}{\sigma }_s^2\text{d}s}={\displaystyle \underset{j=1}{\overset{90}{\sum }}{x}_j^2=\text{0}\text{.00570789}}$ (13)

由于表1中前两款区间金融理财产品其理财期限为62天，从而我们还需要积分波动率 ${\displaystyle {\int }_0^{62/365}{\sigma }_s^2\text{d}s}$。

选取2016年8月12日的数据(共计45个)，重复上面的分析，我们有62天的积分波动率

${\displaystyle {\int }_0^{62/365}{\sigma }_s^2\text{d}s}={\displaystyle \underset{j=1}{\overset{62}{\sum }}{x}_j^2=0.00411275}$ (14)

注意人民币金融理财产品的投资年限不长，见表1，同时又因为我国人民币贷款利率短期内不会发生变化，从而我们以六个月以内的商业贷款利率为无风险利率，即

$r=1.1\%$ (15)

将公式(13)公式(14)以及公式(15)确定的各参数数值代入公式(8)可得各种到期区间金融理财产品的价格，见表6。

Table 6. Hook in the csi 300 index range due to price of financial products

表6. 挂钩于沪深300指数的到期区间金融理财产品的价格

由表6可以看出如果投资期限是62天，金钥匙·如意组合2016年第283期沪深300指数到期窄幅波动人民币金融理财产品价格高；如果投资期限是90天，金钥匙·如意组合2016年第284期沪深300指数到期宽幅波动人民币金融理财产品价值更高。

基金项目

贵州省科学技术基金项目(No.黔科合J字[2015]2076)，贵州省教育厅青年科技人才成长项目(No.黔教KY字[2016]168)。