方孔蜂窝蓄热体内复杂传热的三维CFD研究

3D CFD Study on Complex Heat Transfer in Honeycomb Regenerator with Square Openings

摘要: 采用ANSYS Fluent软件建立了方孔蜂窝陶瓷蓄热体内非稳态流固耦合传热的单元流道模型；以低热值燃料蓄热式燃烧为背景，对蓄热体内烟气、空气与骨架间复杂传热进行了三维数值模拟；预测了各种蓄热体长度下空气预热温度、蓄热体效能和压力损失等热流体性能，并据此进行结构优化；在此基础上研究蓄热体变流量条件下的传热和流动特性。此外，借助温度云图对蓄热式传热机理进行了分析。

Abstract: The unit channel model of square opening ceramic honeycomb regenerator is constructed with ANSYS Fluent for the unsteady conjugate heat transfer. The three-dimensional simulation on the complex heat transfer between the hot flue gas or cool air and solid skeleton in regenerators is made for the application of regenerative burners with low-caloric fuels. The thermal and hydraulic performances such as the preheated air temperature, regenerator effectiveness and flow re-sistances are predicted and the regenerator length is optimized. Besides, the performance char-acteristics at various flow rates are researched on the optimal regenerator. Moreover, the regen-erative heat transfer mechanism is analyzed with temperature contours.

1. 引言

蓄热式燃烧是一项节能环保技术，在各种工业窑炉中得到了广泛应用 [1] [2] [3] [4] [5] 。蓄热式换热器是这种先进燃烧装置的关键部件之一，工作时高温烟气与常温空气以逆流形式周期性依次流过蓄热骨架，传热过程比较复杂 [5] 。与陶瓷小球相比，蜂窝陶瓷作为蓄热骨架能在保证传热性能基础上大幅度减小流动阻力 [6] 。除了实验以外 [7] [8] [9] [10] ，国内外学者对蜂窝蓄热体内部流动传热性能进行了数值模拟研究，比如，陈维汉和罗海兵从圆孔蜂窝中抽取单元结构，建立了二维轴对称的非稳态传热数值模型 [11] 。Rafidi和Blasiak采用钢玉和堇青石制作复合方孔蜂窝蓄热体，并在假定流动充分发展进而具有理论抛物线形速度场的基础上建立了二维数值模型 [12] 。Doh等借助商业软件CFX进行了整机数值模拟研究 [13] ，他们采用不到3万网格模拟1/4的蓄热体，计算结果与实验值相差比较大。值得指出，上述蓄热体研究都是针对高温空气燃烧开展的。在另一方面，工业生产产生大量低热值燃料，借助蓄热式技术，用烟气余热加热助燃空气，可以使这些燃料的燃烧变得稳定和充分。与高温空气燃烧相比，低热值燃料燃烧的空气过剩系数通常较大，其排烟温度较低且受到凝酸的限制，需要进行专门研究。当前商业CFD软件广泛用于各种换热器的数值模拟研究 [14] [15] [16] [17] [18] ，但蓄热式换热器由于存在冷热流体周期性切换，使用CFD软件模拟的研究报道不多。为此，本文拟在对ANSYS Fluent二次开发的基础上，建立方孔蜂窝蓄热体复杂传热的数值模型，并针对低热值燃料蓄热式燃烧应用开展三维数值模拟，分析蓄热体内烟气、空气与固体骨架间的非稳态耦合传热，研究蓄热体长度等参数对传热和流动性能的影响，并在结构优化的基础上研究蓄热体变流量条件的工作特性。

2. 数值模型

2.1. 物理模型

本次数值研究采用高效堇青石方孔蜂窝蓄热体，方孔边长2.07 mm，壁厚0.43 mm。鉴于低热值燃料燃烧温度较低，烟气和空气进口温度分别为673 K和285 K [12] ，两者切换时间为30 s或60 s；空气进口速度为1.95 m/s，对应烟气进口速度5.53 m/s。考虑到增加蓄热体长度，排烟温度下降，可能低于酸露点温度，为此作者在100 mm到200 mm间选择5种长度进行研究。

2.2. 控制方程

蓄热体内部为典型的非稳态流固耦合传热。由于方孔尺寸小，内部流动为层流；由于烟气温度不高，忽略辐射换热；由于流体速度不大，忽略动能和粘性耗散的影响；蓄热体长度适中，烟气凝酸影响不计。基于上述假设，蓄热体内工作流体和固体骨架的能量守恒方程分别表示为：

${\rho }_{f}C{p}_f\frac{\partial T_f}{\partial t}+{\rho }_{f}C{p}_f\left(u\cdot \nabla \right)T_f=\nabla \cdot \left(k_f\nabla T_f\right)$ (1)

$\frac{\partial \left({\rho }_{s}C{p}_s{T}_s\right)}{\partial t}=\nabla \cdot \left(k_s\nabla T_s\right)$ (2)

其中t和T分别代表时间和温度；ρ，k和Cp分别表示密度、热导率和定压比热；下标f和s分别代表流体和固体；u指流体速度，由Navier-Stokes方程组确定，即

${\rho }_f\frac{\partial u}{\partial t}+{\rho }_f\left(u\cdot \nabla \right)u=-\nabla p+\nabla \cdot \left[{\mu }_f\left(\nabla u+\nabla u^{\text{T}}-\frac{2}{3}\nabla \cdot uI\right)\right]$ (3)

$\frac{\partial {\rho }_f}{\partial t}+\nabla \cdot \left({\rho }_{f}u\right)=0$ (4)

其中，p和μ_f分别代表流体压力和动力粘度。

2.3. 数值方案和后处理

考虑到新型蜂窝蓄热体方孔通道均匀布置，本文采用一个截取的对称单元结构来代表整个蓄热体，以减少数值计算工作量。对称单元结构由方孔通道和周围骨架组成，如图1所示。

Figure 1. Cell channel structure and computation grids of honeycomb regenerator with square openings

图1. 方孔蜂窝蓄热体单元通道与计算网格

单元结构的热端为质量流量边界，冷端则采用压力出口边界；流体和固体界面为耦合传热面。控制微分方程组采用ANSYS Fluent数值求解。烟气和空气均为不可压缩理想流体，通过用户自定义函数来描述其热导率、粘度与温度的函数关系，以及两种流体的切换。迭代计算收敛判据是质量和动量方程相对残差小于1e-04，能量方程小于1e-07。通过4套网格验证网格无关性，经过综合评估计算负荷和预测精度，最终模型约14万网格，时间步长为1 s。

3. 热流体性能

蜂窝蓄热体工作足够长时间后，其内部传热和流动将达到周期性稳态，空气预热温度就等于此阶段空气预热周期离开蓄热体的平均温度，即

${\bar{T}}_{ao}={\displaystyle {\int }_{\tau }^{2\tau }\text{d}t}{\displaystyle {\int }_0^A{\left(\rho u_{z}T\right)|}_{z=0}\text{d}S}/{\displaystyle {\int }_{\tau }^{2\tau }\text{d}t}{\displaystyle {\int }_0^A{\left(\rho u_z\right)|}_{z=0}\text{d}S}$ (5)

其中t = τ表示空气预热周期初始时刻；A代表热端(z = 0)的横截面积；u_z为流体轴向速度。

蓄热体效能(ε)等于其实际传热量(Q)与最大可能传热量(Q_max)之比 [12] ，即

$\epsilon =\frac{Q}{Q_{\max }}=\frac{h_{ao}-h_{ai}}{h_a\left(T=T_{gi}\right)-h_{ai}}$ (6)

其中h表示流体比焓；下标g和a分别代表烟气和空气，i和o则分别代表进口和出口。

能量回收率(ERR)表示蓄热体实际回收能量值与最多可能利用能量值之比，即

$ERR=\frac{{\rho }_a{q}_{Va}\left(h_{ao}-h_{ai}\right)}{{\rho }_g{q}_{Vg}\left[h_{gi}-h_g\left(T=T_{ai}\right)\right]}$ (7)

其中q_V代表体积流量。

蓄热体流阻性能由烟气周期平均压力损失和空气周期平均压力损失两部分组成，即 $\overline{\Delta p_g}$ 和 $\overline{\Delta p_a}$ 。

4. 模型验证

为了评价上述CFD模型的预测精度，本文对Rafidi和Blasiak的蓄热体 [12] 进行三维数值模拟，并将典型工况性能的计算值与文献中的实验值和模拟值进行比较，见表1所示。从表1可以看出，切换时间(τ)等于30 s或60 s时，本文模型预测的温度效率( ${\eta }_T=\left({\bar{T}}_{ao}-T_{ai}\right)/\left(T_{gi}-T_{ai}\right)$ )均与实验值非常接近，相对偏差比文献 [12] 模型预测的小。另外，作者监测了蓄热体工作时冷端和热端的流体温度，发现它们均以2 τ为周期不断变化，具体数值与文献 [12] 一致。通过上述比较，可以认为本文CFD模型计算可靠，且有足够精度。

Table 1. The comparison between the predicted values and the literature values

表1. 本文模型预测值与文献值的比较

5. 计算结果及分析

5.1. 蓄热式换热分析

为便于分析烟气通过蓄热骨架向空气传热的物理机制，我们提取蓄热体周期性稳定后不同时刻的温度云图来进行讨论。图2(a)~图2(f)分别描绘了蓄热体(含工作流体)在t = 5 s、15 s、25 s、35 s、45 s、55 s时刻的温度分布情况，其中，空气–烟气切换时间等于30 s，t = 0 s则指烟气周期初始时刻。

从图2(a)，图2(b)和图2(c)可以看到，在烟气周期，随着高温烟气不断进入，蓄热体内流体和骨架温度不断升高，且前者温度总高于后者。这表明烟气将部分热量转移到骨架。另外，随着骨架温度上升，烟气放热速率减慢，出口温度上升。空气预热周期温度场见图2(d)，图2(e)和图2(f)，其变化规律与烟气周期相反，即随着空气不断进入蓄热体，流体和骨架温度都在下降，且前者温度总低于后者，这表明骨架将烟气周期蓄存的热量转移到空气中。另外，随着骨架温度降低，空气得热速率减慢，出口温度降低。

5.2. 蓄热体长度对热流体性能的影响

本文对100 mm和200 mm间5个不同长度(L)的蓄热体在30 s和60 s两个切换时间(τ)下进行了三维

Figure 2. Temperature contours of symmetry plane at various moments

图2. 蓄热体对称面不同时刻温度云图

数值模拟，其中空气进口温度285 K，进口速度(u_a) 1.95 m/s；烟气进口温度673 K，进口速度5.53 m/s。数值计算得到了蓄热体的传热和流动阻力性能，其中不同长度的蓄热体的空气预热温度( ${\bar{T}}_{ao}$ )，以及在经过一定长度的蓄热体后的烟气出口温度( ${\bar{T}}_{go}$ )见图3(a)所示。从图3(a)可以看出， ${\bar{T}}_{ao}$ 随着L的增加而增加， ${\bar{T}}_{go}$ 的变化趋势相反；延长τ， ${\bar{T}}_{ao}$ 下降， ${\bar{T}}_{go}$ 则上升，且τ的影响随L增加而变弱。图3(b)给出了上述5种蓄热体的效能(ε)和能量回收率(ERR)。对比图3(a)和图3(b)，可以看出，ε和ERR的变化规律与 ${\bar{T}}_{ao}$ 相同，即随L的增加而增加，随着τ的增加而减小。当τ = 30 s时，随着L从100 mm增加到200 mm，ε和ERR分别从~76.7%，61.8%增加到~86.0%和69.3%；蓄热体长200 mm时，将τ延长到60 s，ε和ERR分别减少了~1.3%和1.04%，但在L = 100 mm时，两参数减少值分别为~16.15%和13.01%。

上图曲线变化趋势可用蓄热体非稳态传热来解释。随着长度L增加，相同时间内烟气传递给骨架的热量增多，空气也因此从骨架获得更多热量。另一方面，随着流体(烟气或空气)不断流过蓄热体，流体与骨架的温差逐渐减少，这导致热流量随切换时间(τ)的延长而减少。因此，增加L，或者减小τ， ${\bar{T}}_{ao}$ 会升高， ${\bar{T}}_{go}$ 则降低，与图3(a)相一致。鉴于流体温度越高，比焓越大，由式(6)和(7)可知，L越长，或τ越小，蓄热体ε和ERR越大，与图3(b)中曲线一致。

图3(c)给出了烟气和空气压力损失( $\overline{\Delta p_g}$ 和 $\overline{\Delta p_a}$ )随蓄热体长度(L)的变化情况。可以看出，切换时间(τ) = 30 s时，随着L从100 mm增加到200 mm， $\overline{\Delta p_g}$ 和 $\overline{\Delta p_a}$ 分别近乎线性地从83.9 Pa和59.9 Pa增加到155.7 Pa和125.3 Pa，显然，压力损失的这种线性增长是符合粘性流体层流流动的一般规律 [19] 。另一方面，压力损失与τ的关系较复杂，将τ从30 s延长到60 s， $\overline{\Delta p_g}$ 增加了3.6%，而 $\overline{\Delta p_a}$ 减少了7.9%。这种变化规律可以解释如下：

(a) 空气预热温度( ${\bar{T}}_{ao}$ )和烟气出口温度( ${\bar{T}}_{go}$ ) (b) 效能(ε)和能量回收率(ERR)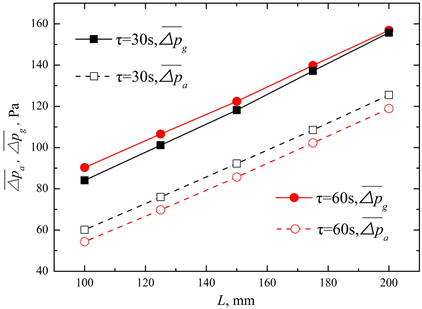(c) 烟气和空气压力损失( $\overline{\Delta p_g}$ 和 $\overline{\Delta p_a}$ )

Figure 3. Effect of regenerator length (L) on heat transfer and flow resistance

图3. 蓄热体长度(L)对传热及流阻性能的影响

延长τ，相同时间切换次数越少，流体换向的局部损失越少，这将使压力损失减小。另一方面，根据图3(a)，τ变大后，烟气出口温度上升，流体速度变大，这可能导致 $\overline{\Delta p_g}$ 增大，所以 $\overline{\Delta p_g}$ 随τ的变化取决于上述两种因素的综合效果；空气预热温度随τ增加而降低，因而 $\overline{\Delta p_a}$ 随τ的增加单调减小。

5.3. 结构优化与变流量特性

增加蓄热体长度，有助于提高余热回收的效率，但烟气出口温度( ${\bar{T}}_{go}$ )降低。 ${\bar{T}}_{go}$ 下降到限制温度时，蓄热体出口容易出现凝酸腐蚀。金属管式空气预热器的 ${\bar{T}}_{go}$ 一般不低于140℃~150℃ [20] 。本文采用的是耐高温热腐蚀的陶瓷材料， ${\bar{T}}_{go}$ 不低于120℃。考虑到蓄热体工作流量偏离额定值后，实际 ${\bar{T}}_{go}$ 可能进一步降低，为此，作者优选长度150 mm的蜂窝蓄热体，并据此针对不同空气流速(烟气流速相应变化)开展变流量特性研究。

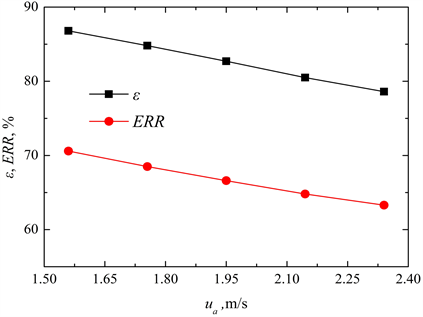
图4(a)示出切换时间30s条件下空气预热温度( ${\bar{T}}_{ao}$ )和烟气出口温度( ${\bar{T}}_{go}$ )随空气进口速度(u_a = 1.56~2.34 m/s，对应80%~120%额定流量)的变化情况。从图中曲线可以看出，随着u_a从额定值的80%增加到120%， ${\bar{T}}_{ao}$ 从622.7 K降低到590.7 K， ${\bar{T}}_{go}$ 则从396.9上升到424.5 K，高于前面定义的 ${\bar{T}}_{go}$ 下限(120℃或393.15 K)。与 ${\bar{T}}_{ao}$ 相似，蓄热体效能(ε)和能量回收率(ERR)随u_a的增加而减少，见图4(b)。就本文所研究的变工况条件，蓄热体ε和ERR的相对变化均小于~9.5%。蓄热体烟气和空气压力损失随工作流量的变化情况见图4(c)所示。从图中曲线可以看到，随着u_a从额定值的80%增加到120%，两流体压力损失分别增加了53%和46%。

(a) 空气预热温度( ${\bar{T}}_{ao}$)和烟气出口温度( ${\bar{T}}_{go}$ ) (b) 效能(ε)和能量回收率(ERR)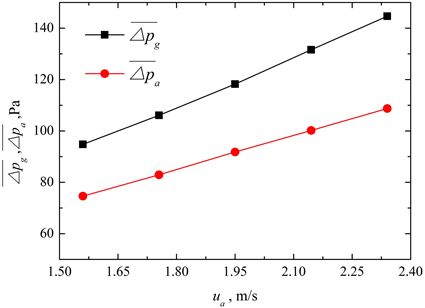(c) 烟气和空气压力损失( $\overline{\Delta p_g}$ 和 $\overline{\Delta p_a}$ )

Figure 4. Regenerator performances of heat transfer and flow resistance under various flow rates (air velocity u_a)

图4. 蓄热体变流量(空气速度u_a)条件下传热和流动性能

6. 总结和结论

本文以低热值燃料蓄热式燃烧应用为背景，通过对CFD软件ANSYS Fluent二次开发，建立方孔蜂窝陶瓷蓄热体复杂传热的单元流道模型，并开展相关三维数值模拟研究，结果表明：

1) 随着蓄热体长度(L)的增加，空气预热温度( ${\bar{T}}_{ao}$ )、蓄热体效能(ε)和能量回收率(ERR)均增大，烟气和空气压力损失也相应增加；减小切换时间， ${\bar{T}}_{ao}$ 、ε和ERR升高，L越小，变化越显著。

2) 烟气出口温度( ${\bar{T}}_{go}$ )随L的增加而减小。在防止出口结露酸腐的前提下，150 mm蓄热体传热和流动综合性能最佳，此时 ${\bar{T}}_{ao}$ 、ε和ERR分别为606.1 K、82.7%和66.6%，而烟气 ${\bar{T}}_{go}$ 和压力损失分别为411.2 K和117.9 Pa。

3) 在偏离额定流量~20%条件下， ${\bar{T}}_{go}$ 较额定值降低~14.5 K，ε和ERR则分别增加了~4.2%和3.4%。