基于靶场高速摄影光学系统畸变分析的三次拟合校正研究

Research on Cubic Fitting Correction Based on Distortion Analysis of Optical System in High Speed Range Photography

摘要: 针对靶场高速电视测量系统短焦距大视场的特点，分析了畸变对测量精度的影响；考虑到靶场短焦距光学系统畸变难以克服的问题，采用实验法和图像矫正法，利用视场标校数据、基于最小二乘原理，建立了三次方程拟合的数学模型，对光学系统全视场进行了畸变校正。实验结果表明，该方法能够有效提高短焦距大视场光学系统靶场测量的精度，简便实用，可操作性强。

Abstract: Aiming at the characteristical of short focal length and large view field of high-speed TV mea-surement system in shooting range, the influence of optical system distortion on measurement accuracy is analyzed. Considering that the optical distortion is difficult to overcome, the mathe-matical model of cubic equation fitting is established by experiment and image correction, using field of view calibration data and least square principle, and the distortion correction of optical full field of view is carried out. The results show that this method can effectively improve the optical measurement accuracy of short focal length and large field of view in shooting range, which is simple, practical and operable.

1. 引言

根据航天工程任务的需要，用于跟踪测量箭体垂直起飞段的高速电视测量仪(经纬仪)设备必须具有尽可能大的像方视场，以保证目标完整和清晰成像，一般采用大视场、短焦距的跟踪方式设计理念 [1] [2] 。而这种设计不可避免的存在光学畸变 [3] ：采用高斯成像公式而存在的非线性误差；由于工艺水平限制，光学系统在加工时可能会带来形变；探测器本身排列就不规则等等。所有这些都会造成图像畸变，其经典表现为图像中的物体扭曲、远近比例不协调等失真问题。这些畸变，必将影响光学系统的测角精度 [4] ，进而影响火箭垂直段飞行状态的评估。所以，必须形成有效的修正方法消除畸变。

国内一些科研院所，很早已经对光学镜头畸变校正展开了大量的研究。针对各种光学镜头畸变，已经有相应的畸变校正数学模型 [5] ，在图像畸变处理上也方法各异。文献 [6] 采用了分区处理的思想，将成像靶面分为多个区，对每一个区域进行线性最小二乘法处理得到所需要的参数，文献 [7] 提出了一种分区修正靶面畸变的算法，文献 [8] 根据畸变与焦距、成像高度之间对应的变化规律提出了一种改进的半球形畸变校正模型，文献 [9] 采用了最小二乘法和分型插值曲面法。这些方法不外乎实验法和基于图像的数字校正方法两种。本文同时采用实验法和图像校正法，根据畸变检测装置的标定，测出不同畸变处的真实视场，利用成像关系修正图像的像素坐标误差，进行三次方程拟合建立整个视场的校正数学模型，使用方便，校正精度高。

2. 畸变对测量精度的影响

由于火箭在垂直起飞段的漂移量处理精度要求较高，对跟踪误差的修正一般采用如下模型。

$A^{\prime }=A+\arctan \left(\frac{x}{f\cdot \cos E-y\cdot \sin E}\right)$ (1)

$E^{\prime }=\arcsin \left(\frac{f\cdot \sin E+y\cdot \cos E}{\sqrt{f^2+x^2+y^2}}\right)$ (2)

$f=\frac{180\times 3600\times l}{\text{π}\times K}$ (3)

式中：A'、E'为跟踪误差修正后的方位角、俯仰角，A、E为经纬仪转台方位角、俯仰角，x、y为目标相对于图像原点的脱靶量，f为摄影焦距，K为角分辨率，l为对应角分辨率像元尺寸。

可以看出，在测角精度一定、目标脱靶量提取精度一定的条件下，目标测角值仅受像元角分辨率的影响。

针对一实际的短焦光学系统，f在25 mm、35 mm、50 mm处固定使用。后端相机的分辨率为1280 × 1024，将x和y坐标为(640, 512)处设为坐标原点。在焦距f = 50 mm时测定其不同区域的像元角分辨率。以坐标原点为中心，范围为50 × 50的正方形区域内，其单个像素的平均角分辨率为41，而在视场最边缘的左上、右上、左下、右下，同样对范围为50 × 50的区域，其平均角分辨率分别为38.0，38.3，37.8，38.1，可见视场的中心区域平均角分辨率比视场边缘大将近2，考虑到此设备老化，像素不高、光学系统分辨率一般，目标在视场最边缘时，若不进行角分辨率校正，其角度测量误差最大可达1280 × (38.3 − 37.8) = 640，即10.7'。由此可见，畸变带来的角分辨率误差对最终的测量精度影响非常大，对于短焦光学系统，其带来的误差甚至占所有系统误差的绝大部分。

3. 数据处理及校正方法

3.1. 数据基础处理

Figure 1. Field-of-view coordinates schematic diagram

图1. 视场坐标示意图

以某台的畸变数据为例进行分析。检测中心给出真值坐标表，简图如上图1所示：A和B方向表示方位，C和D方向代表俯仰。分别测量AB轴和CD轴上的位置坐标，得到原始坐标数据。

下面以方位方向为例进行说明，如图2所示。

图2表格中(959.5, 538)是中心点位置，A列和B列是方位原始数据从大到小的排序，C列是各个坐标与方位中心点坐标值(959.5)的差值。D列是检测中心测定的对应坐标点的角度真值(单位为度˚)。E列对D列求逆(当坐标值为正时，不需要求逆)。F列利用成像几何公式 $\tan \left(x\ast pi/180\right)\ast 25.78/0.01$ 求出真值对应的坐标位置，其中25.78 mm为摄像系统焦距，0.01 mm为探测器像元尺寸。

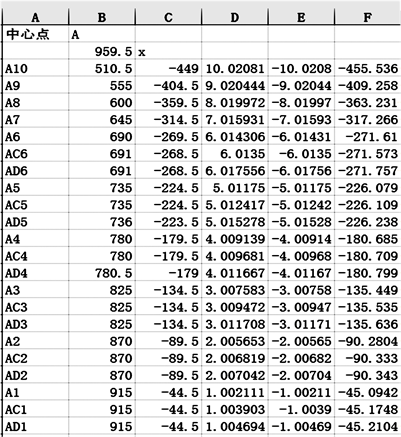
Figure 2. Coordinates and calibration data

图2. 坐标及标定数据

3.2. 三次拟合方程确定

将镜头的各种轴对称像差、非轴对称像差和摄像机感光面的误差考虑在内，从成像角度出发，通过多阶次及多类拟合模型的平稳性评估，最终建立三次多项式摄像系统畸变修正模型。虽然多项式的阶数越高，方程与实际数据拟合程度越高，但阶数越高，计算过程中舍入误差的积累也越大，当阶数n过高时，方程的精度反而会降低，甚至得不到合理的结果。故一般取n = 3∼4 [10] 。

$\{\begin{array}{l}{x}_c=a_3{x}^3+a_2{x}^2+a_{1}x+a_0\\ y_c=b_3{y}^3+b_2{y}^2+b_{1}y+b_0\end{array}$ (4)

式中 $\left(x,y\right),\left(x_c,y_c\right)$ 分别为目标判读点在畸变修正前和修正后的像面坐标； $a_o,a_1,a_2,a_3$ 及 $b_o,b_1,b_2,b_3$ 为修正系数。

$Y={\left\{\begin{array}{c}x{}_{c1}\\ x_{c2}\\ ⋮\\ x_{cn}\end{array}\right\}}_{n\times 1}$ , $X={\left\{\begin{array}{cccc}1& x_{11}& x_{12}^2& x_{13}^3\\ 1& x_{21}& x_{22}^2& x_{23}^3\\ ⋮& ⋮& ⋮& ⋮\\ 1& x_{n1}& x_{n2}^2& x_{n3}^3\end{array}\right\}}_{n\times 4}$ , $a={\left\{\begin{array}{c}a{}_0\\ a_1\\ a_2\\ a_3\end{array}\right\}}_{4\times 1}$

$a=\left\{\begin{array}{c}a{}_0\\ a_1\\ a_2\\ a_3\end{array}\right\}={\left(X^{\text{T}}X\right)}^{-1}{X}^{\text{T}}Y$ (5)

G列求出真值对应坐标和实际坐标的差值dx。以C列为x坐标，F列为y坐标，利用公式(5)得到计算修正系数，H列为由公式(4)得到每个点的拟合值。将拟合结果与实际坐标值相加得到拟合坐标值I列。再利用成像几何公式求解拟合坐标值的对应角度，如J列所示。K列为拟合角度值与真值之间的误差值，单位为秒，单位为度的误差值如L列所示。数据如图3所示。

Figure 3. Processed data

图3. 处理后的数据

俯仰方向的计算方法同方位。

4. 应用效果分析

以某次试验数据为例，对图像成像中的测量点的判读结果进行畸变修正处理。图4(a)、图4(b)分别为像平面上两个坐标方向的数据拟合效果图。

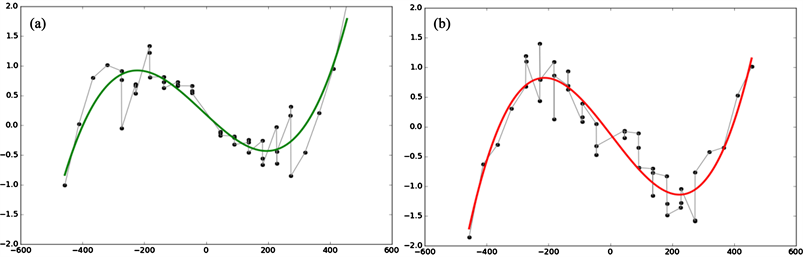
Figure 4. (a) X-direction fitting effect map; (b) Y-direction fitting effect map

图4. (a) X方向拟合效果图；(b) Y方向拟合效果图

通过建立x方向拟 $x_c=0.0000000475x^3-0.0000007507x^2-0.0067576714x-0.1227351960$ ，y方向拟合 $y_c=0.0000000371y^3+0.0000015221y^2-0.0048417881y+0.1792150459$ ，避免了数据大幅度摆动，使得数据更加平稳。

图5(a)~(d)为判读数据畸变修正前后反映到测角数据的比对图。其中图5(a)和图5(b)分别为修正前的角度数据，图5(c)和图5(d)分别为修正后的角度数据。

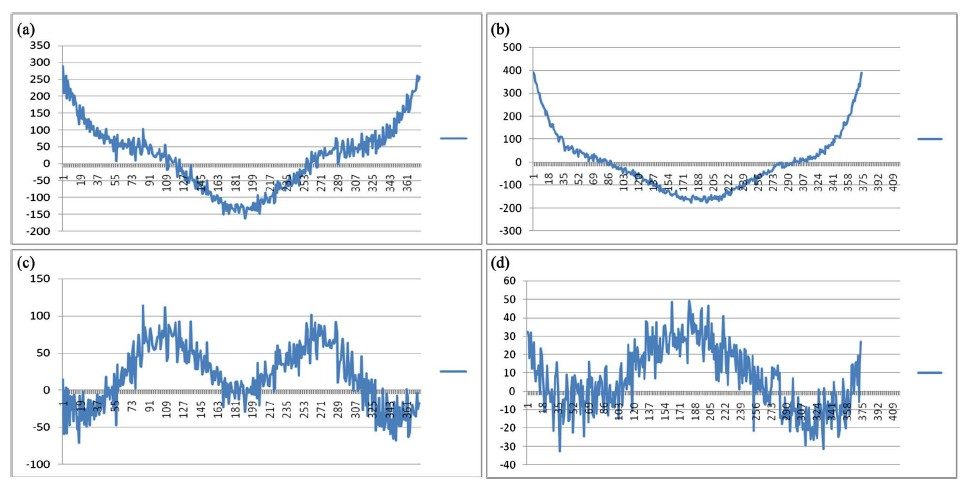
Figure 5. (a) Before distortion correction azimuth error data diagram; (b) Before distortion correction angle of pitch error data diagram; (c) After distortion correction azimuth error data diagram; (d) After distortion correction angle of pitch error data diagram

图5. (a) 畸变修正前方位角误差数据图；(b) 畸变修正前俯仰角误差数据图；(c) 畸变修正后方位角误差数据图；(d) 畸变修正后方位角误差数据图

从图5中可以直观地看出。其中图5(a)的精度为49.63479秒，其中图5(b)的精度为125.8795秒，其中图5(c)的精度为26.36305秒，其中图5(d)的精度为18.65386秒，定性地验证了畸变修正的有效性。

5. 结束语

本文针对目前靶场短焦距大视场光学系统畸变带来测量误差的问题，通过实验数据对光学系统的整个视场进行标定，利用最小二乘原理建立了视场畸变校正的三次方程拟合，对成像的图像像素进行方位和俯仰方向的补偿校正，有效地改善了靶场光学系统测量的精度。该方法原理清晰、过程简洁、简便实用，但在视场标定上，本文还只选取了水平和垂直方向上的测量数据，不同的选取方法可能会对畸变校正有较大的影响，还有待进一步研究。

基金项目

“973”国家重点基础科学研究计划(2011CB302000)；国家自然科学基金重点项目(51232009, 51202299, 61473222, 91646108)；全军重点军事科研计划项目资助。

NOTES

^*通讯作者。