基于PLSR回归模型的黄土区土壤有机质高光谱反演

Inverting Soil Organic Matter from Hyperspectra in Loss Area Soil Based on PLSR Regression Model

摘要: 利用ASD FieldSpec Pro高光谱仪在室内条件下测定了风干土壤样品的可见–近红外光谱，分析了不同土壤深度以及不同植被覆盖下土壤光谱反射率曲线形状变化和土壤有机质含量的变化特点，并针对黄土台塬地区的土壤光谱反射率进行一阶导数、倒数的导数、对数的导数、倒数的对数的导数和对数的倒数的导数的变换，并与土壤有机质含量进行多元逐步回归分析，偏最小二乘回归分析(PLSR)，根据特征光谱段建立多元逐步回归模型以及偏最小二乘回归模型，并验证。综合分析得出，偏最小二乘法在土壤有机质含量高光谱预测研究中更具优势。

Abstract: The visible-near-infrared spectra of air-dried soil samples were determined by ASD FieldSpec Pro hyperspectral spectrometer under indoor conditions. The changes of soil spectral reflectance curve shape and soil organic matter content under different soil depths and different vegetation cover were analyzed, and the loess was analyzed. The spectral reflectance of the soil in the Taihu area is transformed by the first derivative, the derivative of the reciprocal, the derivative of the logarithm, the derivative of the logarithm of the reciprocal and the derivative of the reciprocal of the logarithm, and the multivariate stepwise regression analysis with the soil organic matter content. Least Squares Regression Analysis (PLSR) was established based on the characteristic spectral segments to establish a multivariate stepwise regression model and a partial least squares regression model. The comprehensive analysis shows that the partial least squares method has more advantages in the study of soil organic matter content hyperspectral prediction.

1. 引言

全球碳循环是由很多单一系统组成的，其中陆地生态系统循环是其重要的组成部分，土壤是陆地系统最大的组成元素，土壤独立碳库是陆地系统的最大碳储存库 [1] [2] [3] 。地表附着的植被碳库仅占土壤碳库的1/3，而大气组成的碳库占土壤碳库的1/2 [4] 。同时土壤有机碳库是全球碳库中最活跃的部分之一，又是人类活动可以影响的最大生物圈碳库，任何微小的扰动变化都会影响到土壤与大气碳库之间的碳平衡 [5] [6] [7] 。因此，区域土壤有机碳储量的估算及其动态变化研究具有重要意义。

高光谱数据是现代土壤评价和物理化学性质监测的高效快捷的工具，其具有特征明显的短波红外光谱，并且该技术已得到广泛的应用和推广，比如土壤矿物质元素的定量监测、土壤化学元素含量进行预测反演等 [8] - [15] 。Hanks和Bowers [16] 在1965年研究得出，土壤表面的粗糙度、质地、含水率等都可影响土壤反射率，而且有些物质使通过影响土壤色调进而影响了土壤表面的反射率，如腐殖质。

诸多国内外学者针对土壤光谱与其有机质含量之间的关系进行了大量研究。如Al-bbas等研究发现土壤光谱的反射率与有机质含量之间呈现负相关关系并且关系达到显著 [17] 。Glvos等通过在室内研究土壤光谱与有机质含量的关系，得出土壤反射光谱在550~700 nm处的吸收峰主要是由土壤有机质含量引起的，这一波段时期的敏感特征波段，并且利用AVIRIS高光谱影像资料分析了两者间关系，取得了一些进展 [18] 。

在比利时南部农业区土壤有机质含量的监测中，Toure S、Tychon B利用航空高光谱数据，并且利用建立了有机质与土壤光谱之间良好的逐步回归方程，明确了两者之间的关系，并且取得了满意的反演结果。诸多研究过程都广泛地应用了土壤反射光谱特性，所建立的有机质方程模型具有显著的相关性 [19] 。

最早在20世纪80年代，我国土壤光谱和有机质之间的研究就开始了，主要是将资源卫星光谱图像和统计方法结合，从而得到土壤表层有机质含量的光谱图像四个波段的辐射值函数，对光谱的研究有深远意义 [20] 。谢伯承 [21] 、王静 [22] 、郑立华 [23] 、贺军亮等 [24] 、武彦清 [25] 、杨萍 [26] 、陈红艳 [27] 、李曦 [28] 结合土壤光谱解译和分析，构建估算有机质含量的最佳方程模型，取得长足进展。

目前对于土壤高光谱特性的研究，从国内研究现状来看，针对东北黑土、红壤等的报道较多，而有关黄土台塬地区的研究较少，其高光谱特性有待进一步研究和探明。为了剔除其他因素对光谱响应特征的影响，本文将采集土壤样品进行预处理后，与实验室内测定其光谱数据，通过分析不同光谱变换模式与土壤有机质含量之间的关系，建立多种土壤有机质高光谱反演模型，旨在提高土壤有机质模型精度和稳定性。

2. 材料与方法

2.1. 土样制备

试验土壤于2017年6月采自陕西省永寿县(E 107˚58', N 34˚31')。永寿县地处关中西北部，位于咸阳地区西部，属于暖温带大陆季风气候，冬季长而干燥，夏季短而温和，年均气温10.8℃，极端最高气温38.9℃，平均降雨量601.6 mm，常年主导风向为东南风、西北风。植被属于暖温带落叶阔叶林地带，研究区共分8个土类，即黄土性土、红土、黑垆土、娄土、褐土、石渣土、潮土、淤土。本实验采集的是黄绵土和少量褐土。

供试土壤共有15个采样点，采集土壤深度为0~30 cm。并且实地记载了采样点的形态特征和成土环境条件，同时对各个土层采集土样标本并分析样本。样品在实验室内经过自然风干，使用木棒压磨后去除沙砾和植物残体，然后过2 mm尼龙筛并对其均匀混合，共制备成75个土样共两份。

2.2. 光谱测定

用ASD FieldSpec4高光谱仪(波长范围为350~2500 nm光谱采样间隔约1.5 nm，光谱分辨率为3.5 nm。波长可以精确到1 nm，光纤探头视场角度分别为1˚、7.5˚和10˚。数据处理与常见的TM传感器的波段范围TM1~TM4相结合，分别代表450~520 nm，520~600 nm，630~690 nm，760~900 nm。

是在室内75 W卤素灯光照条件下，采用7.5˚视场角探头，距土壤样品垂直高度为45 cm处采集光谱数据，光源角度为30˚，测量时间范围为上午11:00~12:00。光谱采样每10个为一组，得到土壤反射光谱曲线，进行均值处理。为减小因环境因素造成的误差，在每组测量前后都及时进行了标准白板校正。

2.3. 回归方法

多元线性逐步回归分析主要是对于全部的自变量，按照其对所有因变量的影响或者贡献大小来进行对比分析，并且利用F检验法，选择运用回归的平方和显著的变量进入回归方程，但是每一步回归只需引入1个变量，从而可建立起一个偏回归方程。当变量被引入之后，依次检验各变量的偏回归平方和。当引入新变量后是原来方程中的变量改变为不显著的时候，则将其从偏回归方程中剔除。引入变量超过2个时，开始考虑是否有需要剔除的变量。当方程中所有自变量对所存在的因变量有显著影响的时候则不需要剔除时，再进一步考虑从未引入方程的自变量中挑选具有显著影响的新得变量进入方程。引入和剔除都可作为一步。不断的重复这一过程，直到无法剔除已引入的变量，原自变量也已引入结束，逐步回归方程结束，从而得出逐步回归方程的方程公式为：

$\text{SOM}=a_0+{\displaystyle \underset{i=1}{\overset{N}{\sum }}{a}_i}{R}_{{\lambda }_i}$

其中，SOM为有机质含量， $a_0$ ， $a_i=1$ ，N为回归系数，N为用于建模的波段数， ${\lambda }_i$ 为第i个建模波段的波长， $R_{{\lambda }_i}$ 为波长 ${\lambda }_i$ 处的反射率值。

偏最小二乘回归(partial least squares regression, PLSR)是考虑p个因变量与m个自变量的建模问题，基本做法是首先在自变量集中提取第1成分x₁，同时在因变量集中提取第1成分u₁，要求x₁和u₁相关程度达到最大。然后建立因变量与x₁的回归，如果回归方程已达到满意的精度，则算法终止。否则继续对第2对成分的提取，直到达到满意的精度为止。若最终对自变量集提取n个成分 $x_1,x_2,\cdots ,x_n$ ，偏最小二乘回归将建立因变量与 $x_1,x_2,\cdots ,x_n$ 的回归式，然后再表示为因变量与原自变量的回归方程式，即偏最小二乘回归方程式。

2.4. 模型检验方法

用于模型校准的评价参数主要有：决定系数(R²)、均方根误差(RMSE)、标准校准误差(Standard Error of Calibration, SEC)、标准预测误差(Standard Error of Prediction, SEP)、预测偏差(Bias)、观测值标准偏差(SD)、相对误差(RE)与标准预测误差的比值RPD等。本文研究主要用到决定系数(R²)、均方根误差(RMSE)。

1) 决定系数(R²)

$R^2=\frac{{\displaystyle \underset{i=1}{\overset{N}{\sum }}{\left({\hat{Y}}_i-\bar{Y}\right)}^2}}{{\displaystyle \underset{i=1}{\overset{N}{\sum }}{\left(Y_i-\bar{Y}\right)}^2}}$

其中， $Y_i$ 为实测值， $\bar{Y}$ 为实测值的平均值， ${\hat{Y}}_i$ 为预测值，N为样本数。

2) 均方根误差(RMSE)

$RMSE=\sqrt{\frac{1}{N}{\displaystyle \underset{i=1}{\overset{N}{\sum }}{\left({\hat{Y}}_i-Y_i\right)}^2}}$

其中， $Y_i$ 为实测值， ${\hat{Y}}_i$ 为预测值，N为样本数。

对不同的建模集和验证集分别进行验证。建模集均方根误差(RMSE)越小，决定系数(R²)越大，说明模型越稳定，模型精度越好；而验证集均方根误差(RMSE)越小，决定系数(R²)说明预测效果越好。另外从模型的预测能力来看，对于建模精度较好的模型并不一定同时具有较好的有机质含量预测能力。

3. 数据分析

数据预处理

不同的光谱波段对于能量的响应特征存在差异性，光谱曲线存在一些受水汽等影响而产生的噪声，为剔除噪声对数据处理结果的影响，本研究将利用9点加权移动平均方法实现对原始数据的去噪平滑处理。本研究的光谱曲线给出了N个波长的序列( $Ri,i=400,401,402,\cdots ,1000$ )，此时，i的值取为包括前后各4个的加权平均值，即i的新值Ri'用包括这个波长对应反射率在内的9个波长对应的反射率的加权平均值所替代，称为平滑值(图1)。

$Ri\text{'}=0.04R_i-4+0.08R_{i-3}+0.12R_{i-2}+0.16R_{i-1}+0.20R_i+0.16R_i$ $+1+0.12R_{i+2}+0.08R_{i+3}+0.04R_{i+4}$

对测量获取的土壤反射率数据进行初步选择，去除异常数据，选定75条光谱数据，其中随机抽取50条数据用于模型的回归分析，其余25条用于模型验证。

对原数据进行一阶求导、对数的导数、倒数的导数、平方根的导数，通过比较分析原反射率以及其不同的变换方式下(图2)的多元逐步回归模型和偏最小二乘回归模型的建模精度和预测能力。

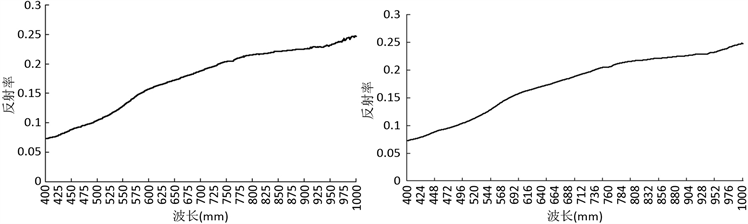平滑前 平滑后

Figure 1. Comparison before and after smoothing

图1. 平滑前后比较

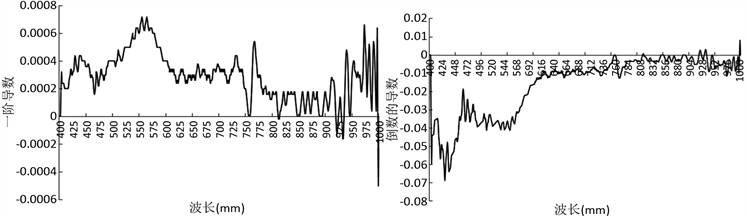
Figure 2. The form of the spectral curve under four transformations

图2. 四种变换下的光谱曲线形式

4. 模型的建立与分析

4.1. 基于多元逐步回归的估测模型

将经平滑去噪后的反射率及其四种的变换后的结果作为输入光谱，采用多元逐步回归分析筛选土壤有机质的显著波段。由表1可知：参与拟合的波段则主要集中在近红外区域。光谱预处理方式不同，显著波段的位置及数量都不一样，进而参与到模型拟合的波段不同。在显著水平设定为0.05的条件下，R、(lgR)'、(1/R)'、R'、(R^1/2)'筛选出的显著波段个数均逐渐的增加，由1个依次增加到10个，且相互有少数的交叉集中波段。各个光谱段的最大方差膨胀因子都小于10，所以光谱段间不存在多重共线性，由以上说明基于原反射率的一阶导数变换所获取的特征波段有助于回归分析，建立模型。

分别将原反射率和4种变换下的特征波普段作为自变量，土壤有机质含量的实测值作为因变量，进行逐步回归分析。设定变量方差贡献显著水平0.05作为选入和剔除变量的标准，建立有机质含量的多元逐步回归估测模型。再通过检验数据对模型进行检验，分析检验模型的拟合优度(R²)和均方根误差(RMSE)确定模型的稳定性以及预测能力。

Table 1. Significant bands of organic matter screened by multiple stepwise regression analysis

表1. 经多元逐步回归分析筛选出的有机质显著波段

表2中表示的是对土壤有机质含量与原始光谱及其数学变换形式进行多元线性逐步回归分析得到的分析结果。5组模型中，基于(R^1/2)'和R'的预测模型的R²最低，基本上无拟合性，说明模型的精度很差；其他四种变换的预测R²处于0.4以上，其中基于(1/R)'的预测R²最高。但基于R'、(1/R)'、(R^1/2)'变换的模型的预测均方根误差(RMSE)都非常的大，稳定性不如(lgR)'、R两种模型。虽然基于(lgR)'的模型其建模的拟合度和模型稳定性都不是最好的，但是综合分析看基于(lgR)'检验模型中其拟合度和稳定性在相对于其他模型是优秀的，可能原因是光谱进行了对数一阶求导后，最大效果的扩大了样本光谱特征之间的差异所致。图3为采用多元线性逐步回归方建模并结合4种不同光谱预处理方法得到土壤有机质含量预测结果图。

Table 2. Results of multiple stepwise regression analysis of soil organic matter content under different transformation forms

表2. 不同变换形式下土壤有机质含量的多元逐步回归分析结果

采用多元线性逐步回归分析法建立的模型中，拟合效果最好的模型其光谱预处理方法为对数的导数((lgR)')变换，所得模型的拟合优度为0.825，均方根误差为2.909，检验决定系数为0.45，检验均方根误差为7.221。该最佳模型中共引入7个波段。

4.2. 基于偏最小二乘回归的估测模型

对五种光谱变换形式进行偏最小二乘回归模型的建立，本次操作使用SIMCA-P统计分析软件。如表3，结果表明，偏最小二乘回归分析得到的PLSR因子数不同，R'、(lgR)'、(R^1/2)'变换下的PLSR因子数为3，(1/R)'的因子数为2。因为原反射率在进行偏最小二乘回归中未提取到主成分因子进行分析，所以

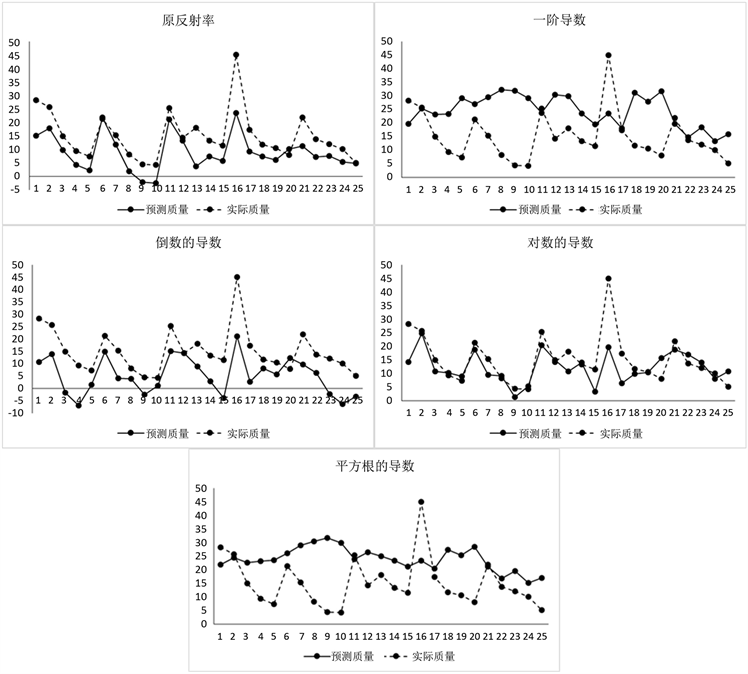
Figure 3. Comparison of predicted and measured organic matter content

图3. 有机质含量预测值与实测值比较

无法建立偏最小二乘回归模型。其余4组偏最小二乘法回归模型中，除基于(1/R)'变换的模型的R²仅为0.58外，另外三种模型R'、(lgR)'、(R^1/2)'的R²都达到了0.74以上，具有比较好的建模解释能力，同时三种模型也具有较好的稳定性，均方根误差RMSE在3.1与3.4之间。在模型检验中，(lgR)'的稳定性变的最差，R²仅为0.45。另外基于R'的模型的检验稳定性相对于(R^1/2)'的模型检验稳定性较差。

偏最小二乘回归法所建立最优模型为反射率的平方根求导变换，选择PLSR因子数为3。该模型的校正决定系数为0.78，均方根误差为3.15；模型的验证决定系数为0.87，均方根误差为1.59。

Table 3. Results of partial least squares regression analysis of different derivative transformation forms and soil organic matter content

表3. 不同导数变换形式与土壤有机质含量的偏最小二乘回归分析结果

注：—表示偏最小二乘回归分析未统计出结果。

用偏最小二乘法进行土壤有机质含量高光谱模型研究结果表明，采用不同的光谱预处理方法，运用PLSR建模方法所得模型的预测效果均较好，说明采用该方法具有稳定性和可靠性(图4)，适用于一定地理区域内土壤有机质含量的高光谱反演。

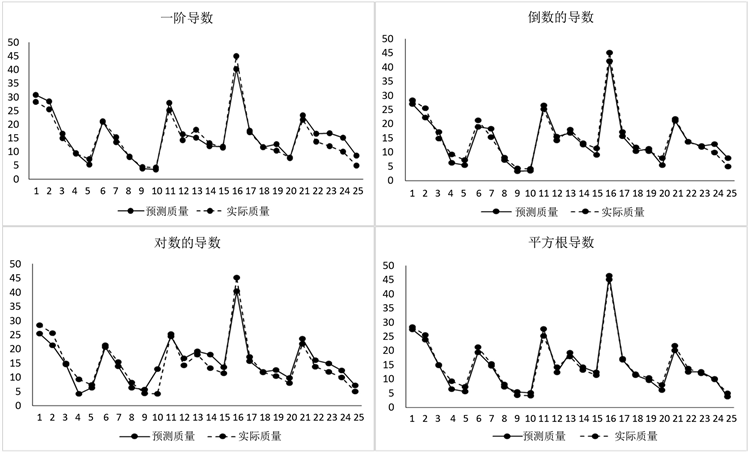
Figure 4. Comparison of predicted and measured organic matter content

图4. 有机质含量预测值与实测值比较

5. 结论

利用多元线性回归分析和偏最小二乘回归建立的有机质高光谱模型预测结果均有效达到了有机质含量的预测精度要求，对比表2和表3可得出，利用多元线性逐步回归对数的导数变换分析得到的优选模型精度高于偏最小二乘回归平方根求导变换模型，且预测效果优良。其中，利用偏最小二乘回归建立的模型，其预测效果对光谱预处理方式的敏感度较小，实现了预测模型精度和稳定较稳定，表现为对于不同方法得到的模型，其RMSE处在4附近徘徊，其变化范围比SMLR法得到的结果(最小值为7.22，最大值14.79)小。这说明偏最小二乘回归在预测黄土台塬地区的典型类型土壤的有机质含量时更具稳定性，可满足应用需求。

黄土台塬地区典型土壤类型的内部结构和理化性质差异较大，同时，土壤光谱受外界环境因素和土壤内部营养元素影响较大，因此，选用合适的光谱前处理方法及稳定的有机质含量预测方法具有至关重要的作用。诸多学者利用高光谱对土壤有机质进行反演和预测时，遴选的敏感波段主要是基于光谱数据与有机质含量之间的相关性分析，依据推算及研究分析，相关性较大的波段多为多元回归分析的自变量。也有一部分学者采用主成分回归分析方法建立有机质含量预测模型，且效果良好。本文选用的偏最小二乘法是在普通多元回归的基础上融入主成分分析，并且结合典型相关分析的思路，基本上解决了自变量间多重共线性问题，最大程度的提取包含自变量更多信息的元素成分，从而保证筛选并提取成分元素与因变量间最大的相关性。综合分析研究表明，偏最小二乘法在土壤有机质含量高光谱预测研究中优势明显。当样本数较少，波段数较多且自相关性强时，偏最小二乘法显示更多的优势，利用该方法可获取更可靠的预测结果。