1. 引言
有限群论是数学的一个分支,是代数学的基础组成部分。迄今为止,有限群论已经日渐完善,但仍有越来越多的问题尚待解决。近几十年,群论中的大多数公开问题及其进展都收集在The Kourovka Notebook系列丛书中,目前已经到第19版,详见 [1] 。在有限群论研究中,一个非常本质的课题是如何理解共轭类,其中Burnside、Poland、Ito等数学家特别从数量角度研究共轭类长对于群结构的影响。关于这方面研究,有一个老而著名的问题,现被称为S3-猜想,见( [1] , 16.3):
S3-猜想:若有限群G的共轭类长度各不相同,则
。
1994年,我国著名有限群论专家张继平教授 [2] 证明了可解情形下S3-猜想。1995年Knörr,Lempken 以及Thielcke [3] 也独立证明了这一情形。要特别提到的是,1994年,Arad,Muzychuk,Oliver [4] 应用特征标理论证明了如果G是S3-猜想的极小反例,那么G的非交换底柱(socle)要么平凡要么同构于下列群之一:
,
,其中
,
。根据单群分类定理以及有限单群的共轭类长,本文主要证明下述定理:
定理1:任一非交换有限单群至少有两个长度相同的共轭类。因此,若非交换有限群G的共轭类长度各不相同,则G非单。
2. 预备知识
为了方便起见,本文用到的已知结论均以引理的形式给出。除特别指出,所用的记号都是标准的,参见 [5] 。
引理2.1:若
,则
,其中
为欧拉函数。
引理2.2:令
,则
,除非
为下列形式:
。
证明:这是( [6] ,引理2)。 □
引理2.3:令
,其中
,则
,除非
下列形式:
。
证明:这是( [6] ,引理3)。 □
引理2.4:令q为素数方幂,l为正整数,则
,除非
为下列形式:
1)
;2)
;3)
;4)
。
证明:这是( [6] ,引理6)。 □
引理2.5:设
或
,则G有一个半单元素,阶为
,并且至多分别共轭
个半单元素的幂。
证明:这是( [7] ,推论3.4)。 □
引理2.6:设
,
是
中所有与
有相同类型置换的集合,考虑
在
中的中心化子
,则:① 当
含有一个奇置换时,
是
的一个共轭类;② 当
不含有奇置换时,
在
中分裂为以下两个长度相同的共轭类:
;
证明:这是( [10] ,定理2.7.6)。 □
3. 有限单群共轭类长
根据单群分类定理,有限非交换单群为以下群之一:离散单群、交错群、李型单群以及Tits单群,详见 [8] 。
3.1. 离散单群与Tits单群
命题3.1:设S为离散单群或Tits单群,则S至少有两个长度相同的共轭类。
证明:根据GAP [9] 直接验证可得,具体如表1。 □
3.2. 交错群共轭类长
命题3.2:对于任意的
,交错群
至少有两个长度相同的共轭类。
证明:当n为奇数时,令
,则
,从而
中不含有奇置换。根据引理2.6,
在
中分裂为长度相同的两个共轭类;当n为偶数时,令
则
,此时
也有两个长度相同的共轭类
与
。命题得证。 □

Table 1. Conjugate class lengths of discrete singletons and Tits singletons with multiplicities of at least 2
表1. 离散单群与Tits单群重数至少为2的共轭类长
3.3. 李型单群的共轭类长
本节我们考察李型单群的共轭类长。李型单群共有16族,其中典型单群为
其中
且
,
其中
且
,
其中
、
其中
、
其中
、
其中
;
例外单群为
其中
,
,
,
,
,
,
,
其中
,
其中
,
其中
。
引理3.3.1:设
,其中
,
是素数p的方幂,则S至少有两个长度相同的共轭类。
证明:注意到
。根据( [6] ,引理17),令
,其中f为正整数。记
是有
个元素的有限域,
为
的乘法群。由有限域的乘法群为循环群,记
为
的生成元,则
,
。令
为
的代数闭包。令G为域
上的
型单的单连通代数群,F为G中Frobenius自同态,并记
为F作用下的有限不动点群,
。记
为
的对偶,则
。
令
,
,其中
,则
。
令
且
为自然同态,即
,
则
,
。已知
,则
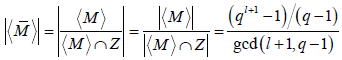 ,
,
即得
。
又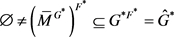 ,那么
在
及
共轭类相交非空。在它们交集中选取半单元素s,
且
,则s最多共轭于
个在
的s的幂,因此对于在
中s的本原方幂至少有
个共轭类,又
,则
。而
,故
。
,那么
在
及
共轭类相交非空。在它们交集中选取半单元素s,
且
,则s最多共轭于
个在
的s的幂,因此对于在
中s的本原方幂至少有
个共轭类,又
,则
。而
,故
。
要证S至少有两个长度相同的共轭类,即要证
而这等价于证明
记
,由引理2.1,2.2可知
。易知
,故S至少有两个长度相同的共轭类,除了下列情况:
及
为下列形式:
对于这些例外情形,可以直接用GAP验证
,从而引理得证。 □
引理3.3.2:设
,其中
,
是素数p的方幂且
,则S至少有两个长度相同的共轭类。
证明:注意到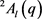 又称
,那么算
的共轭类及其长度,即算
的共轭类及其长度。若
又称
,那么算
的共轭类及其长度,即算
的共轭类及其长度。若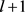 为奇数,令
为
的生成元。
,
,定义
,则当l为奇数时,
为奇数,令
为
的生成元。
,
,定义
,则当l为奇数时,
当l为偶数时,
即
。令
,则
,从而
。
令
,由引理2.3可知,
,从而
。因此S至少有2个长度相同的共轭类,除非
为下列形式:
。而对于这些例外情形,利用GAP直接验证可得当
为
时
。对于剩余情形,即
或
,
运行GAP程序可知
有两个长度为40的共轭类;
有两个长度为3360的共轭类;
有两个长度为1774080的共轭类。又由于
可解无需考虑,故引理得证。 □
引理 3.3.3. 设
,其中
,
是素数p的方幂且
,则S至少有两个长度相同的共轭类。
证明:
又称
或
,求
共轭类及其长度即求
共轭类及其长度。令
,根据( [7] ,推论3.4)在G中包含一个半单元素s,且
,对于
,有
个生成元,则s至多共轭于
个s的方幂。则s的本原方幂至少有
个共轭类,即
个共轭类,下证
。
由( [6] ,引理6)易知,
,除非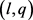 为下列形式:
为下列形式:
1)
;
2)
;
3)
;
4)
,若
,则结论成立;对于
的情况,即
或
。
运行GAP程序可知
有2个长度为40的共轭类、
共轭类长度为40的重数大于2、
共轭类长度为255的重数大于2、
共轭类长度为13,000的重数大于2、
共轭类长度为13,000的重数大于2、
共轭类长度为262,080的重数大于2、
共轭类长度为13,000的重数大于2,即
至少有两个长度相同的共轭类。故引理得证。□
引理3.3.4:设
,其中
,
是素数p的方幂,则S至少有两个长度相同的共轭类。
证明:
又称
、
,求
共轭类及其长度即求
共轭类及其长度。令
,根据( [7] ,推论3.4),在G中包含一个半单元素s,且
,对于
有
个生成元,则s至多共轭于
个s的方幂。则s的本原方幂至少有
个共轭类,即
个共轭类,下证
。
根据( [6] ,引理6)易知,
,除非
为下列形式:
1)
;
2)
;
3)
;
4)
,若
则结论成立;对于
的情况,即
或
。
运行GAP程序可知
共轭类长度为7560的重数至少为2;
共轭类长度为364的重数至少为2;
共轭类长度为514,080的重数至少为2。即
有两个不同的共轭类长度相同。故引理得证。 □
引理3.3.5:设
,其中
,
是素数p的方幂,则S至少有两个长度相同的共轭类。
证明:
又称
、
,求
共轭类及其长度即求
共轭类及其长度。令
,根据( [7] ,推论3.4),在G中包含一个半单元素s,且
,对于
,有
个生成元,则s至多共轭于
个s的方幂。则s的本原方幂至少有
个共轭类,即
个共轭类,下证
。
根据( [6] ,引理6)易知,
,除非
为下列形式:
1)
;
2)
;
3)
;
4)
,若
则结论成立;对于
的情况,即
运行GAP程序可知在
共轭类长度为3780的重数至少为2。即
有两个不同的共轭类长度相同,引理得证。 □
引理3.3.6:设
,其中
,
是素数p的方幂,则S至少有两个长度相同的共轭类。
证明: 又称
,求
共轭类及其长度即求
共轭类及其长度。令
,根据( [7] ,推论3.4),在G中包含一个半单元素s,且
,对于
,有
个生成元,则s至多共轭于
个s的方幂。则s的本原方幂至少有
个共轭类,即
个共轭类,下证
。
又称
,求
共轭类及其长度即求
共轭类及其长度。令
,根据( [7] ,推论3.4),在G中包含一个半单元素s,且
,对于
,有
个生成元,则s至多共轭于
个s的方幂。则s的本原方幂至少有
个共轭类,即
个共轭类,下证
。
根据( [6] ,引理6)易知,
,除非
为下列形式
1)
;
2)
;
3)
;
4)
,若
则结论成立;对于
的情况,即
或
,
运行GAP程序可知在
共轭类长度为9,400,320的重数至少为2、
共轭类长度为268,632的重数至少为2、
共轭类长度为609,280的重数至少为2。即
有两个不同的共轭类长度相同,引理得证。 □
引理3.3.7:设
,其中
是素数p的方幂,则S至少有两个长度相同的共轭类。
证明:当
,则由( [11] , p. 409),
有两个不同的共轭类
,其长度为
;
当
,则由( [12] ,p. 239,表VII-1),
有
个不同的共轭类,其中
,则有至少两个不同的共轭类
,长度为
;
当
,
非单,无需考虑,当
时,由( [13] ,p. 364,表IV-1),
有
个不同的共轭类
,长度为
,引理得证。 □
引理3.3.8:群
至少有两个长度相同的共轭类,其中
是素数p的方幂。
证明:根据 [14] 可知,当
时,群
有
个不同的共轭类,它们的长度相同;当时
时,群
有
个不同的共轭类,它们的长度相同。下设
。当
时,运行GAP可知,此时群
至少有两个不同的共轭类,它们的长度相同,为69615。当
时,同样根据 [14] 可知,群
至少有
个不同的共轭类,它们的长度相同。引理得证。 □
引理3.3.9:设
,其中
是素数p的方幂,则S至少有两个长度相同的共轭类。
证明:根据 [14] 可知,当
时,群
有
个不同的共轭类,它们的长度相同;当
时,群
有
个不同的共轭类,它们的长度相同。下设
,由 [14] 另一数据可知,此时群
至少有
不同的共轭类,它们的长度相同,GAP运行得为共轭类长度为136592595114393600。当
时,同样根据 [14] 可知,群
至少有
个不同的共轭类,它们的长度相同。由此引理得证。 □
引理3.3.10:设
,其中
是素数p的方幂,则S至少有两个长度相同的共轭类。
证明:根据 [14] 可知,当
时,群
有
个不同的共轭类,它们的长度相同;当
时,群
有
个不同的共轭类,它们的长度相同。下设
,由 [14] 另一数据可知,此时群
至少有
不同的共轭类,它们的长度相同,运行GAP程序得共轭类长度为96543730483200;当
,由 [14] 另一数据可知,此时群
至少有
不同的共轭类,它们的长度相同。故引理得证。 □
引理3.3.11:群
至少有两个长度相同的共轭类,其中
是素数p的方幂。
证明:对于
,根据 [14] 可知,当
时,群
有
个不同的共轭类,它们的长度相同。当
时,群
有
个不同的共轭类。下面考虑
,当
时,根据 [14] 另一张表格可知,群
有
个不同的共轭类,它们的长度相同。当
时,根据 [14] 可知有531个共轭类,有两个元素中心化子的阶为
,则
至少有两个不同的共轭类,它们的长度相同。故引理得证。□
引理3.3.12:群
至少有两个长度相同的共轭类,其中
是素数p的方幂。
证明:对于
,根据文献 [14] 可知,
当
时,群
有
个不同的共轭类,它们的长度相同。当
时,群
有
个不同的共轭类。当
时,根据文献 [14] 另一张表格可知,群
有
个不同的共轭类,它们的长度相同。当
时,根据文献 [14] 可知,
至少有两个不同的共轭类,它们的长度相同。引理得证。 □
引理3.3.13:群
至少有两个长度相同的共轭类,其中
是素数p的方幂。
证明:对于
,根据( [18] ,p. 53,表4.4)可知,其中心化子的阶为
当q为偶数时,重数为
当q为奇数时,重数为
那么它们至少有2个共轭类长度相同。引理得证。 □
引理3.3.14:设
,其中
,则S至少有两个长度相同的共轭类。
证明:对于任意群G中的元素x及其逆元素
有
且
根据( [16] , p. 87)可知,群
有非实元素
有
,但
位于不同的共轭类,它们所在的共轭类长度相同,即
至少有两个共轭类长度相同,由此引理得证。 □
引理3.3.15:设
,其中
,则S至少有两个长度相同的共轭类。
证明:同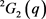 的做法,根据( [17] , p. 143, 定理13),群
有元素
,位于不同的共轭类,它们所在的共轭类长度相同。引理得证。 □
的做法,根据( [17] , p. 143, 定理13),群
有元素
,位于不同的共轭类,它们所在的共轭类长度相同。引理得证。 □
引理3.3.16:设
,其中
,则S至少有两个长度相同的共轭类。
证明:根据( [15] ,p. 7,表2),在
中有元素
,
,
,
,它们中心化子的阶相同均为
。
由群
阶为
可知,其共轭类长度相同为
,
即
至少有两个共轭类长度相同,从而引理得证。 □
命题3.3:任意李型单群至少有两个长度相同的共轭类。
证明:由引理2.3.1.~2.3.16即得。 □
定理1的证明:根据有限单群分类定理以及命题3.1~3.3即得。 □