二维矢量多极孤子和涡旋孤子探究

Research on Two-Dimensional Vector Multipole Solitons and Vortex Solitons

摘要: 本文研究了二维耦合具有空间的非线性薛定谔方程调制非线性和横向调制，推导并分析矢量多极孤子和涡旋孤子解。当选择调制深度取0和1时，分别得到矢量多极孤子和涡旋孤子结构。方位角裂片的数量(多个极化孤子的“花瓣”)由拓扑指数m确定，多极孤子中的层数通过n值确定。

Abstract: In this paper, two-dimensional coupled nonlinear Schrödinger equations with spatial nonlinear modulation and lateral modulation are studied, and vector multipole and vortex soliton solutions are derived and analyzed. When the modulation depth is selected to be 0 and 1, the vector multi-pole and vortex soliton structures are obtained, respectively. The number of azimuthal lobes (the “petal" of a plurality of polarized solitons) is determined by the topological index m, and the number of layers in the multipole soliton is determined by the value of n.

1. 研究背景

与具有一个分量的空间标量孤子相比，具有两个或更多个分量的空间矢量孤子在非线性介质中相互自陷。由于它们的多组分结构，矢量孤子的动态传播行为比标量孤子的动态传播行为更丰富。考虑到多分量结构，需要考虑N个场的光孤子的同时传播，并且控制方程变为耦合非线性薛定谔方程 [1] 。当两个不同频率的光波在介质中共同传播并通过介质非线性地相互作用时，或者当两个极化分量在某个中心频率处非线性相互作用时，两个问题的传播方程可以用Manakov方程 [2] 来描述。具有相等自相位调制和交叉相位调制的Manakov矢量孤子可以以亮–亮，亮–暗和暗–暗的三种形式传播。此外，Manakov矢量孤子在束缚态中以匀速传播也已被研究。然而，这些工作都讨论的是一维空间矢量孤子。

据研究所知，二维空间矢量孤子的讨论相对较少。最近，基于二维Manakov方程，Kerr介质中标量和矢量偶极孤立波的自陷已被研究。与空间标量孤子相比，空间矢量孤子在光束衍射控制、逻辑门设计、光学开关器件和信息变换等方面有更多的应用 [3] [4] 。涡旋孤子是在配备光子晶格的光折变晶体中产生的。众所周知，由于二维设置中局域立方自吸收非线性的关键特性，二维 Kerr介质中的固定孤子总是不稳定以防止坍塌或衰减。然而，由于介质非线性响应的复杂性，这些研究几乎完全通过数值方法进行，并且尚未报道局域矢量涡旋的解析解。相对解析解，数值解的分析较为容易，但也存在瓶颈，这些数值解往往和数值分析时的种子解的模式类似，所以出现不了新的涡旋结构，而且模式较单一，多为单环模式。

最近几年，由于近代孤子理论的发展和现代光学材料中折射率可调介质的引入，矢量涡旋孤子的(准)解析研究也成为了涡旋孤子理论研究热门。A. S. Desyatnikov [5] 等人在非局域非线性克尔介质和饱和非线性介质中解析并数值分析了拉盖尔–高斯型空间调制涡旋光孤子的动力学特征和稳定性，包括高拓扑指数情况。O. V. Borovkova [6] 等人发现，在不需要外势的束缚下，空间不均匀自散焦非线性能够支持所有维度的亮孤子解析解，只要非线性强度向边缘增长得足够快。在国内，涡旋孤子解析研究也成为涡旋稳定性研究的热点。郭旗课题组大量研究强非局域介质(介质响应函数的宽度远大于光束束宽)中孤子传输问题，其中戴继慧等人研究了旋转的惠特克函数型空间调制涡旋光孤子。研究表明，在一定的条件下，旋转的惠特克函数型调制涡旋孤子演变为拉盖尔–高斯型涡旋孤子，或退化为角向无强度变化的圆对称型涡旋光孤子，并提出涡旋旋转角速度由传播常数和调制参量共同决定。

本文运用近代孤子理论获得在局域Kerr介质中的二维解析的多极孤子和涡旋孤子，并研究了这些孤子的结构模式。

2. 理论模型及形变约化

基于上述原因，将关注以下具有变系数的耦合二维非线性薛定谔方程 [7]

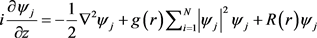(1)

其描述了由在Kerr介质中共同传播的N个互不相干分量组成的矢量光束，其折射率为 $n=n_0+n_{1}R\left(r\right)+n_{2}g\left(r\right){\left|\psi \right|}^2$ 。在这个等式中， ${\psi }_j\left(z,r,\phi \right)\left(j=1,2,\cdots ,N\right)$ 是缓慢变化的包络线，其传播距离z和横向平面中的极坐标r和 $\phi$ ， ${\nabla }^2$ 为二维拉普拉斯算子，克尔非线性系数g(r)以及横向调制R(r)被假定为径向坐标 $r\equiv \left(x,y\right)$ 的函数。横向x，y和纵向z坐标归一化为波束宽度 $w_0={\left(2k_0^2{n}_1\right)}^{-1/4}$ ，衍射长度 $L_d=k_0{w}_0^2$ ，在输入波长 $\lambda$ 处波数 $k_0=2\text{π}{n}_0/\lambda$ 。对于消失的横向调制(即 $R\left(r\right)=0$ )，方程(1)可以被认为是马纳科夫系统的二维形式。如果ψ_j表示凝聚物的宏观波函数，则R(r)表示外电势，方程(1)耦合了玻色–爱因斯坦凝聚体中的Gross-Pitaevskii方程。

空间非均匀非线性(SIN)和横向调制已被广泛讨论。然而，尚未报道局域矢量涡旋的解析解。接下来，寻找方程(1)的空间局部固定精确解

${\psi }_j\left(r,\phi ,z\right)=A\left(r\right){\Phi }_j\left(\phi \right)\exp \left(-i\kappa z\right)$ (2)

其中 $\kappa$ 是传播常数， $A\left(r\right)$ 为局域函数，满足 ${\lim }_{r\to \pm \infty }A\left(r\right)=0$ 。

将式(2)代入方程(1)，可得

$\frac{r^2}{A}\left\{\frac{{\partial }^{2}A}{\partial r^2}+\frac{1}{r}\frac{\partial A}{\partial r}+2\left[\kappa -R\left(r\right)\right]A-2g\left(r\right)A^3\right\}=m^2$ (3)

$-\frac{1}{{\varphi }_j}\frac{{\partial }^2{\varphi }_j}{\partial {\phi }^2}=m^2$ (4)

函数 ${\varphi }_j$ 满足自洽条件 ${\displaystyle {\sum }_{j=1}^N{\left|{\varphi }_j\right|}^2}=1$ 。

方程(4)有以下形式解

${\Phi }_j=C_j\cos \left(m\phi \right)+D_j\sin \left(m\phi \right)$ (5)

其中m可以被认为是拓扑指数。这里，考虑双组分情况(N = 2)，因此 $C_1=1$ ， $D_1=ip$ ， $C_2=0$ ， $C_2=\sqrt{1+p^2}$ ，其中调制深度 $p\left(0\le p\le 1\right)$ 。极限值分别表示多极(p = 0)和涡旋(p = 1)孤子，拓扑指数m =1~5表示偶极子、四极子、六极子、八极子和十二极孤子。

将 $A\left(r\right)=\rho \left(r\right)U\left[\chi \left(r\right)\right]$ 代入方程(3)，且 $U\left[\chi \left(r\right)\right]$ 满足

$-\frac{{\text{d}}^{2}U}{\text{d}{\chi }^2}+G\left(U\right)=\eta U$ (6)

可得

${\rho }_{rr}+\frac{1}{r}{\rho }_r+\left[2\kappa -2R\left(r\right)-\frac{m^2}{r^2}\right]\rho =\frac{\eta }{r^2{\rho }^3}$ (7)

$$ ， $\frac{G\left(U\right){\chi }_r^2}{U^3}-2g{\rho }^2=0$ (8)

其中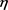和g₀是常数。

方程(8)中增益及非线性项满足

$g\left(r\right)=G\left(U\right)r^{-2}{\rho }^{-6}\left(r\right)/\left(2U^3\right)$ ， $\chi \left(r\right)={\displaystyle {\int }_0^r{\rho }^{-2}\left(s\right)s^{-1}\text{d}s}$ (9)

从以上过程，耦合的NLSE(1)被简化为可解的平稳NLSE(6)，由于静态NLSE(6)具有丰富的解，所以方程形变有助于找到新型精确解。例如雅可比椭圆函数解。因此，方程(7)的可解性对于构建耦合NLSE(1)的精确解至关重要。

方程(7)不容易解决。首先，考虑更简单的情况，即在方程(7)中 $\eta =0$ 。在这种情况下，对于 $R\left(r\right)=\omega r^2$ 的抛物横向调制外势，可得精确解为

$\rho =r^{-1}\left[c_{1}M\left(\frac{\kappa }{2\sqrt{2\omega }},\frac{m}{2},\sqrt{2\omega }{r}^2\right)+c_{2}W\left(\frac{\kappa }{2\sqrt{2\omega }},\frac{m}{2},\sqrt{2\omega }{r}^2\right)\right]$ (10)

函数 $M(\cdot )$ 和 $W(\cdot )$ 分别是惠特克的M和W函数。

若横向调制势消失，即 $R\left(r\right)=0$ ，有

$\rho =c_{3}J\left(m,\sqrt{2\kappa }r\right)+c_{4}Y\left(m,\sqrt{2\kappa }r\right)$ (11)

函数 $J(\cdot )$ 和 $Y(\cdot )$ 分别为第一类和第二类贝塞尔函数。

注意，SIN强度是有界的，并且 $R\left(r\right)$ 中的积分收敛，因此 $R\left(r\right)$ 和 $g\left(r\right)$ 的表达式要求 $\rho$ 不能改变其符号，并且它必须表现为 $r^{-\gamma }$ ，当 $r\to 0$ 时 $\gamma \ge 1/3$ ， $r\to \infty$ 时 $\rho \to \infty$ (发散)。这些限制要求表达式(10)中的 $c_1{c}_2>0$ ， $\kappa <{\kappa }_0\equiv 2\left(1+m\right)\sqrt{\omega }$ ，且式(11)中 $c_3{c}_4>0$ ， $\kappa <0$ 。

此外，如果 $\eta =0$ ，则 $\rho \left(r\right)$ 的解变为

$\rho =\sqrt{\frac{1}{r}\left(\alpha {\varphi }_1^2+2\beta {\varphi }_1{\varphi }_2+\gamma {\varphi }_2^2\right)}$ (12)

其中 $\alpha ,\beta ,\gamma$ 为常数， $\eta =\left(\alpha \gamma -{\beta }^2\right)W^2$ ， $W={\varphi }_1{\varphi }_{2r}-{\varphi }_2{\varphi }_{1r}$ ， ${\varphi }_1\left(r\right)$ 和 ${\varphi }_2\left(r\right)$ 是方程

${\varphi }_{rr}+\left[2\kappa -2R\left(r\right)-\frac{m^2}{r^2}\right]\varphi =0$

两个线性无关的解。

将方程(1)形变为方程(6)，这里提供了一种系统的方法，在“孤波海洋”中找到无数个新的精确“孤子岛”。方程(1)的解由方程(6)的解生成。方程(6)中G(U)的广泛选择使其成为一些著名方程，如薛定谔方程，NLSE，sine-Gordon方程，KdV方程，从而构造了方程的丰富解。例如，如果 $G\left(U\right)$ 是U的线性函数，则方程(6)是具有外势的线性薛定谔方程。当外势为谐波和双曲线电势时，方程的解已被用于构建局部模式。如果 $G\left(U\right)=g_0{U}^3$ ，则边界条件满足 $U\left(0\right)=U\left(\infty \right)=0$ ，且在 $\eta =0$ 时，可得以下精确解为

$U\left(\chi \right)=\frac{2n\lambda }{\sqrt{-g_0}}sd\left[2n\lambda \chi \left(r\right),\frac{\sqrt{2}}{2}\right]$ (13)

其中 $g_0<0$ ，函数 $sd(\cdot )\equiv sn(\cdot )/dn(\cdot )$ 与雅可比椭圆正弦函数 $$ 和雅可比椭圆第三类函数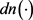，孤子序数 $n=1,2,3,\cdots$ ，和 $\lambda =K\left(\frac{\sqrt{2}}{2}\right)$ ，具有第一类完全椭圆积分K(k)，k为模数。

3. 矢量多极孤子和涡旋孤子结构

在没有 $R\left(r\right)=0$ 的横向调制的情况下，对于p = 0，m = 1，n = 1，解表现为矢量偶极子孤子。对于p = 0，解为具有不同m和n值的多极孤子。所有多极孤子的强度在中心处等于零。多极孤子的方位角波瓣(“花瓣”)的数量由2m的值确定，并且多极孤子中的层数由n的值确定。根据方位角波瓣(“花瓣”)的数量，多极孤子分别称为四极和六极孤子。对于相同的n，随着值m的增加，结构在径向方向上扩展。类似地，对于相同的m，增加值n最外层中的“花瓣”也在径向方向上扩展。

当考虑抛物横向调制 $R=\omega r^2$ 时，可构造矢量多极孤子和涡旋孤子。对于p = 0，两个正交排列的矢量偶极孤子分量也非相干叠加以产生环孤子。涡旋孤子围绕其核心具有2π相位的跳跃。

存在抛物线横向调制 $R=\omega r^2$ 的情况下，对于相同的n，该结构也随着值m的增加而在径向方向上扩展，并且对于相同的m，在该m中的“花瓣”最外层也在径向方向上扩展，增加值n。比较多极孤子，在存在抛物线横向调制 $R=\omega r^2$ 的情况下，多极孤子在径向方向上扩展得比在没有横向调制的情况下扩展得更宽，是抛物横向调制势的效果抵消了非线性的影响，使得非线性的影响减弱了。因此，在存在抛物横向调制势的情况下，多极孤子的图案在径向方向上具有更宽的空间。

4. 小结

本文研究了具有空间调制非线性和横向调制的二维耦合非线性薛定谔方程，并导出了解析向量多极孤子和涡旋孤子解。当调制深度q被选择为0和1时，分别构造矢量多极孤子和涡旋孤子。多极孤子的方位角裂片(“花瓣”)的数量由拓扑指数m确定，并且多极孤子中的层数由孤子序数n的值确定。本文获得的矢量涡旋解析解有助于提高涡旋的稳定性。孤子稳定性分析非常重要，只有所求的涡旋孤子是稳定的，才能对实验及现实的应用有着积极的意义。对于涡旋孤子，到目前为止还没有人提出统一的稳定性判据，涡旋稳定性必须针对于不同介质模型独立解决。由于涡旋引入的拓扑指数(角动量的存在)，使得涡旋孤子稳定性的要求远远大于单纯的空间孤子。研究调制非线性介质中的涡旋孤子解的具体解析模式，就可以研究系统中参数对涡旋孤子存在窗口、涡核半径、振幅、能量等进行调控的问题，以及涡旋对称破缺不稳定性的抵消条件，进而研究涡旋光束或涡旋孤子在多种介质非线性响应下的传输及其稳定性问题。