一类二阶非线性微分方程解的零点存在性

The Existence of Zero-Points of Solution for a Class of Second Order Nonlinear Differential Equation

摘要: 本文研究了一类二阶非线性微分方程。通过建立几个微分不等式，建立了方程解的零点存在的若干新条件，并通过实例说明定理的有效性。

Abstract: In the present paper, we investigate a class of second order differential equation. By establishing several inequalities, some new conditions on the existence of zero-points of solution for the equation are obtained. Several examples are given to illustrate the effectiveness of the obtained conditions.

1. 引言

微分方程解的零点分布是研究微分方程解的性态的一个重要课题,也是微分方程振动理论的基础。1836年，Sturm C. F.针对二阶微分方程建立了解的零点比较定理 [1] ，并把相关理论推广到其它类型的微分方程和差分方程。1910年，Mauro Picone通过证明一个恒等式——Picone恒等式，进一步推广了Sturm零点比较定理 [2] 。自此，利用类似思想，通过建立新的Picone型恒等式或不等式，Sturm零点比较定理得以更进一步的推广，用以讨论各类更复杂的二阶微分方程的解或解的导函数的零点分布 [3] - [8] 。如陈丽纯，庄容坤研究了方程

${\left(p\left(t\right)\Psi \left(y\right)k\left(y^{\prime }\right)\right)}^{\prime }+r\left(t\right)k\left(y^{\prime }\right)+q\left(t\right)f\left(y\right)=0$ (1.1)

解的零点存在性。郑镇汉，李亚兰研究了方程

${\left(p\left(y^{\prime }\right)\right)}^{\prime }+r\left(t\right)y^{\prime }+q\left(t\right)y=f\left(t,y,y^{\prime }\right)$ (1.2)

解的零点存在性。

受上述研究工作的启发，本文考虑方程

${\left(p\left(t\right)\varphi \left(y\right)k\left(y^{\prime }\right)\right)}^{\prime }+r\left(t\right)k\left(y^{\prime }\right)+q\left(t\right)y=f\left(t,y,y^{\prime }\right)，$ (1.3)

其中 $p\in C^1\left(\left[0,1\right];R_{+}\right)$ ， $r\in C\left(\left[0,1\right];R\right)$ ， $q\in C\left(\left[0,1\right];R_{+}\right)$ ， $f\in C\left(\left[0,1\right]\times R\times R;R\right)$ ， $k,\varphi \in C^1\left(R;R\right)$ 。通过建立几个微分不等式，建立非线性方程(1.3)解的零点存在的几个新的充分条件，并通过例子说明所得结果的有效性。

2. 几个不等式

为了证明主要结果，本节先证明几个微分不等式。往下总假设以下条件成立：

(A1) $\text{0}<C_1\le \varphi \left(y\right)\le C_2,y\in R$ ；

(A2) $k^2\left(y\right)\le C_{3}yk\left(y\right),y\in R$ 。

引理1 设 $y\left(t\right)$ 是方程(1.3)的非平凡解， $x\left(t\right)\in C^1\left(\left[0,1\right];R\right)$ ，若 $y\left(t\right)\ne 0,t\in \left[0,1\right]$ ，则成立下面的微分不等式：

$\begin{array}{c}{\left(-\frac{x^{2}p\varphi \left(y\right)k\left(y^{\prime }\right)}{y}\right)}^{\prime }\ge {\left(\sqrt{\frac{p\varphi \left(y\right)}{C_3}}\frac{xk\left(y^{\prime }\right)}{y}+\sqrt{\frac{C_3}{p\varphi \left(y\right)}}\frac{r\left(t\right)x}{2}-\sqrt{C_{3}p\varphi \left(y\right)}{x}^{\prime }\right)}^2\\ -\frac{C_3}{4C_{2}p}{\left[2C_{2}p{x}^{\prime }-r\left(t\right)x\right]}^2\\ +\frac{1}{4C_2{C}_{1}p}\left(4C_2{C}_{1}pq+C_3\left(C_1-C_2\right)r^2\right)x^2-\frac{f\left(t,y,y^{\prime }\right)x^2}{y}.\end{array}$ (2.1)

证明 直接求导，并结合 ${\left(p\varphi \left(y\right)k\left(y^{\prime }\right)\right)}^{\prime }=f\left(t,y,y^{\prime }\right)-r\left(t\right)k\left(y^{\prime }\right)-q\left(t\right)y$ 及条件(A1)和(A2)得：

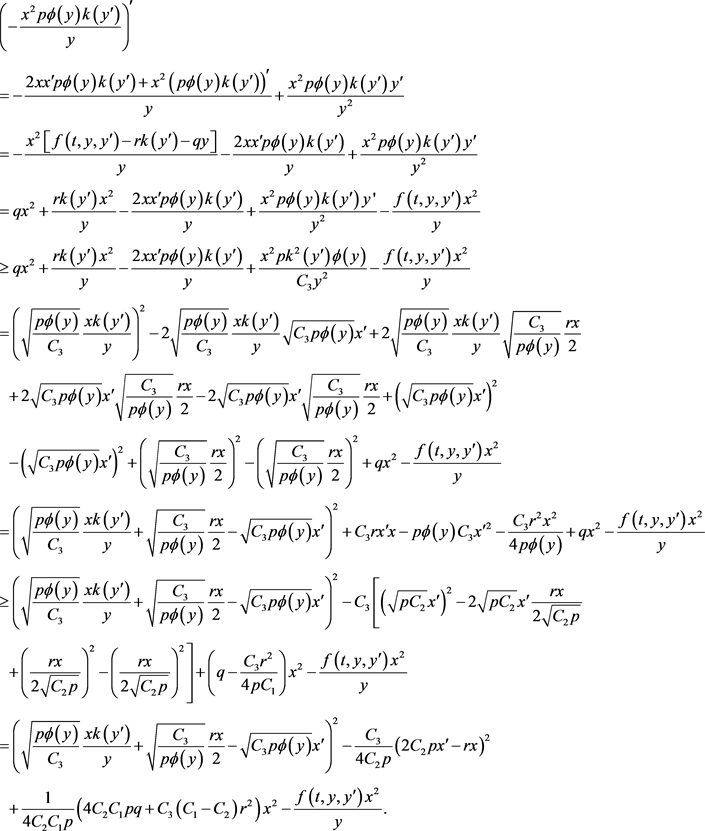
证毕。

引理2 设 $y\left(t\right)$ 是方程(1.3)的非平凡解， $x\left(t\right)\in C^1\left(\left[0,1\right];R\right)$ ，若 $y\left(t\right)\ne 0,t\in \left[0,1\right]$ ，则成立下面的微分不等式：

${\left(-\frac{x^{2}p\varphi \left(y\right)k\left(y^{\prime }\right)}{y}\right)}^{\prime }\ge q{x}^2+\frac{p\varphi \left(y\right)}{C_3}{\left(C_3{x}^{\prime }-\frac{xk\left(y^{\prime }\right)}{y}\right)}^2-C_2{C}_{3}p{x^{\prime }}^2+\frac{rk\left(y^{\prime }\right)-f\left(t,y,y^{\prime }\right)}{y}{x}^2.$ (2.2)

证明 由引理1的证明及条件(A1)和(A2)得：

$\begin{array}{l}{\left(-\frac{x^{2}p\varphi \left(y\right)k\left(y^{\prime }\right)}{y}\right)}^{\prime }\\ \ge q{x}^2+\frac{rk\left(y^{\prime }\right)x^2}{y}-\frac{2x{x}^{\prime }p\varphi \left(y\right)k\left(y^{\prime }\right)}{y}+\frac{x^{2}p\varphi \left(y\right)k^2\left(y^{\prime }\right)}{C_3{y}^2}-\frac{f\left(t,y,y^{\prime }\right)x^2}{y}\\ =q{x}^2+\frac{p\varphi \left(y\right)}{C_3}{\left(C_3{x}^{\prime }-\frac{xk\left(y^{\prime }\right)}{y}\right)}^2+\frac{rk\left(y^{\prime }\right)x^2}{y}-C_{3}p\varphi \left(y\right){x^{\prime }}^2-\frac{f\left(t,y,y^{\prime }\right)x^2}{y}\\ \ge q{x}^2+\frac{p\varphi \left(y\right)}{C_3}{\left(C_3{x}^{\prime }-\frac{xk\left(y^{\prime }\right)}{y}\right)}^2-C_2{C}_{3}p{x^{\prime }}^2+\frac{rk\left(y^{\prime }\right)-f\left(t,y,y^{\prime }\right)}{y}{x}^2.\end{array}$

证毕。

引理3 设 $y\left(t\right)$ 是方程(1.3)的非平凡解， $x\left(t\right)\in C^1\left(\left[0,1\right];R\right)$ ，若 $y\left(t\right)\ne 0,t\in \left[0,1\right]$ ，则成立微分不等式：

$\begin{array}{c}{\left(-x^{2}W\left(t\right)\right)}^{\prime }\ge C_2{C}_{3}p\left(t\right)\Phi \left(t\right){\left(\frac{W\left(t\right)}{C_2{C}_{3}p\left(t\right)\Phi \left(t\right)}x-x^{\prime }-\frac{1}{2}\bar{R}\left(t\right)x\right)}^2\\ -C_2{C}_{3}p\left(t\right)\Phi \left(t\right){\left(x^{\prime }+\frac{1}{2}\bar{R}\left(t\right)x\right)}^2+Q\left(t\right)x^2-\frac{f\left(t,y,y^{\prime }\right)}{y}\Phi \left(t\right)x^2.\end{array}$ (2.3)

其中 $\Phi \left(t\right),R\left(t\right)\in C^1\left(\left(0,+\infty \right);R\right)$ ， $W\left(t\right)=\Phi \left(t\right)p\left(t\right)\left[\frac{\varphi \left(t\right)k\left(y^{\prime }\right)}{y}+R\left(t\right)\right]$ ， $\bar{R}\left(t\right)=\frac{2R\left(t\right)}{C_2{C}_3}+\frac{{\Phi }^{\prime }\left(t\right)}{\Phi \left(t\right)}-\frac{r\left(t\right)}{C_{2}p\left(t\right)}$ ， $Q\left(t\right)=\Phi \left(t\right)\left[q\left(t\right)-\frac{C_3\left(C_2-C_1\right)}{4C_1{C}_2}\frac{r^2\left(t\right)}{p\left(t\right)}-\frac{r\left(t\right)}{C_2}R\left(t\right)+\frac{p\left(t\right)}{C_2{C}_3}{R}^2\left(t\right)-{\left(p\left(t\right)R\left(t\right)\right)}^{\prime }\right]$ 。

证明 由 ${\left(p\varphi \left(y\right)k\left(y^{\prime }\right)\right)}^{\prime }=f\left(t,y,y^{\prime }\right)-r\left(t\right)k\left(y^{\prime }\right)-q\left(t\right)y$ 及条件(A1)和(A2)得：

$\begin{array}{l}{W}^{\prime }\left(t\right)=\frac{{\Phi }^{\prime }\left(t\right)}{\Phi \left(t\right)}W\left(t\right)+\Phi \left(t\right)\left[{\left(\frac{p\left(t\right)\varphi \left(y\right)k\left(y^{\prime }\right)}{y}\right)}^{\prime }+{\left(p\left(t\right)R\left(t\right)\right)}^{\prime }\right]\\ =\frac{{\Phi }^{\prime }\left(t\right)}{\Phi \left(t\right)}W\left(t\right)+\Phi \left(t\right)\left[\frac{f\left(t,y,y^{\prime }\right)-r\left(t\right)k\left(y^{\prime }\right)-q\left(t\right)y}{y}-\frac{p\left(t\right)\varphi \left(y\right)k\left(y^{\prime }\right)y^{\prime }}{y^2}+{\left(p\left(t\right)R\left(t\right)\right)}^{\prime }\right]\\ \le \frac{{\Phi }^{\prime }\left(t\right)}{\Phi \left(t\right)}W\left(t\right)+\Phi \left(t\right)\left[\frac{f\left(t,y,y^{\prime }\right)}{y}-\frac{r\left(t\right)k\left(y^{\prime }\right)}{y}-q\left(t\right)-\frac{p\left(t\right)\varphi \left(y\right)k^2\left(y^{\prime }\right)}{C_3{y}^2}+{\left(p\left(t\right)R\left(t\right)\right)}^{\prime }\right]\\ =\frac{{\Phi }^{\prime }\left(t\right)}{\Phi \left(t\right)}W\left(t\right)+\Phi \left(t\right)\{-q\left(t\right)+{\left(p\left(t\right)R\left(t\right)\right)}^{\prime }+\frac{f\left(t,y,y^{\prime }\right)}{y}\\ -\frac{1}{\varphi \left(y\right)}\left[\frac{r\left(t\right)\varphi \left(y\right)k\left(y^{\prime }\right)}{y}+\frac{p\left(t\right)}{C_3}{\left(\frac{\varphi \left(y\right)k\left(y^{\prime }\right)}{y}\right)}^2\right]\}\end{array}$

$\begin{array}{l}=\frac{{\Phi }^{\prime }\left(t\right)}{\Phi \left(t\right)}W\left(t\right)+\Phi \left(t\right)\{-q\left(t\right)+\frac{C_3\left(C_2-C_1\right)}{4C_1{C}_2}\frac{r^2\left(t\right)}{p\left(t\right)}+\frac{r\left(t\right)}{C_2}R\left(t\right)-\frac{p\left(t\right)}{C_2{C}_3}{R}^2\left(t\right)\\ +{\left(p\left(t\right)R\left(t\right)\right)}^{\prime }+\left(\frac{2R\left(t\right)}{C_2{C}_3\Phi \left(t\right)}-\frac{r\left(t\right)}{C_2\Phi \left(t\right)p\left(t\right)}\right)W\left(t\right)-\frac{W^2\left(t\right)}{C_2{C}_3{\Phi }^2\left(t\right)p\left(t\right)}+\frac{f\left(t,y,y^{\prime }\right)}{y}\}\\ =\frac{{\Phi }^{\prime }\left(t\right)}{\Phi \left(t\right)}W\left(t\right)-\Phi \left(t\right)\left[q\left(t\right)-\frac{C_3\left(C_2-C_1\right)}{4C_1{C}_2}\frac{r^2\left(t\right)}{p\left(t\right)}-\frac{r\left(t\right)}{C_2}R\left(t\right)+\frac{p\left(t\right)}{C_2{C}_3}{R}^2\left(t\right)-{\left(p\left(t\right)R\left(t\right)\right)}^{\prime }\right]\\ +\left(\frac{2R\left(t\right)}{C_2{C}_3}-\frac{r\left(t\right)}{C_{2}p\left(t\right)}\right)W\left(t\right)-\frac{W^2\left(t\right)}{C_2{C}_3\Phi \left(t\right)p\left(t\right)}+\frac{f\left(t,y,y^{\prime }\right)}{y}\Phi \left(t\right)\\ =-\Phi \left(t\right)\left[q\left(t\right)-\frac{C_3\left(C_2-C_1\right)}{4C_1{C}_2}\frac{r^2\left(t\right)}{p\left(t\right)}-\frac{r\left(t\right)}{C_2}R\left(t\right)+\frac{p\left(t\right)}{C_2{C}_3}{R}^2\left(t\right)-{\left(p\left(t\right)R\left(t\right)\right)}^{\prime }\right]\\ +\left(\frac{2R\left(t\right)}{C_2{C}_3}+\frac{{\Phi }^{\prime }\left(t\right)}{\Phi \left(t\right)}-\frac{r\left(t\right)}{C_{2}p\left(t\right)}\right)W\left(t\right)-\frac{W^2\left(t\right)}{C_2{C}_3\Phi \left(t\right)p\left(t\right)}+\frac{f\left(t,y,y^{\prime }\right)}{y}\Phi \left(t\right)\\ =-Q\left(t\right)+\bar{R}\left(t\right)W\left(t\right)-\frac{W^2\left(t\right)}{C_2{C}_3\Phi \left(t\right)p\left(t\right)}+\frac{f\left(t,y,y^{\prime }\right)}{y}\Phi \left(t\right).\end{array}$

因此，

$\begin{array}{l}{\left[-x^{2}W\left(t\right)\right]}^{\prime }\\ \ge -2x{x}^{\prime }W\left(t\right)-x^2\left(-Q\left(t\right)+\bar{R}\left(t\right)W\left(t\right)-\frac{W^2\left(t\right)}{C_2{C}_{3}p\left(t\right)\Phi \left(t\right)}+\frac{f\left(t,y,y^{\prime }\right)}{y}\Phi \left(t\right)\right)\\ ={\left(\frac{W\left(t\right)}{\sqrt{C_2{C}_{3}p\left(t\right)\Phi \left(t\right)}}x\right)}^2-2\frac{W\left(t\right)x}{\sqrt{C_2{C}_{3}p\left(t\right)\Phi \left(t\right)}}\sqrt{C_2{C}_{3}p\left(t\right)\Phi \left(t\right)}{x}^{\prime }\\ -2\frac{W\left(t\right)x}{\sqrt{C_2{C}_{3}p\left(t\right)\Phi \left(t\right)}}\frac{\sqrt{C_2{C}_{3}p\left(t\right)\Phi \left(t\right)}}{2}\bar{R}\left(t\right)x+{\left(\sqrt{C_2{C}_{3}p\left(t\right)\Phi \left(t\right)}{x}^{\prime }\right)}^2\\ -{\left(\sqrt{C_2{C}_{3}p\left(t\right)\Phi \left(t\right)}{x}^{\prime }\right)}^2+{\left(\frac{\sqrt{C_2{C}_{3}p\left(t\right)\Phi \left(t\right)}}{2}\bar{R}\left(t\right)x\right)}^2-{\left(\frac{\sqrt{C_2{C}_{3}p\left(t\right)\Phi \left(t\right)}}{2}\bar{R}\left(t\right)x\right)}^2\end{array}$

$\begin{array}{l}+2\left(\sqrt{C_2{C}_{3}p\left(t\right)\Phi \left(t\right)}{x}^{\prime }\right)\left(\frac{\sqrt{C_2{C}_{3}p\left(t\right)\Phi \left(t\right)}}{2}\bar{R}\left(t\right)x\right)\\ -2\left(\sqrt{C_2{C}_{3}p\left(t\right)\Phi \left(t\right)}{x}^{\prime }\right)\left(\frac{\sqrt{C_2{C}_{3}p\left(t\right)\Phi \left(t\right)}}{2}\bar{R}\left(t\right)x\right)+Q\left(t\right)x^2-\frac{f\left(t,y,y^{\prime }\right)}{y}\Phi \left(t\right)x^2\\ ={\left(\frac{W\left(t\right)}{\sqrt{C_2{C}_{3}p\left(t\right)\Phi \left(t\right)}}x-\sqrt{C_2{C}_{3}p\left(t\right)\Phi \left(t\right)}{x}^{\prime }-\frac{\sqrt{C_2{C}_{3}p\left(t\right)\Phi \left(t\right)}}{2}\bar{R}\left(t\right)x\right)}^2\\ -{\left(\sqrt{C_2{C}_{3}p\left(t\right)\Phi \left(t\right)}{x}^{\prime }+\frac{\sqrt{C_2{C}_{3}p\left(t\right)\Phi \left(t\right)}}{2}\bar{R}\left(t\right)x\right)}^2\\ +Q\left(t\right)x^2-\frac{f\left(t,y,y^{\prime }\right)}{y}\Phi \left(t\right)x^2\end{array}$

$\begin{array}{l}=C_2{C}_{3}p\left(t\right)\Phi \left(t\right){\left(\frac{W\left(t\right)}{C_2{C}_{3}p\left(t\right)\Phi \left(t\right)}x-x^{\prime }-\frac{1}{2}\bar{R}\left(t\right)x\right)}^2\\ -C_2{C}_{3}p\left(t\right)\Phi \left(t\right){\left(x^{\prime }+\frac{1}{2}\bar{R}\left(t\right)x\right)}^2+Q\left(t\right)x^2-\frac{f\left(t,y,y^{\prime }\right)}{y}\Phi \left(t\right)x^2.\end{array}$

证毕。

3. 主要结果

本节利用上节得到的不等式建立几个零点存在定理。

定理1 设 $y\left(t\right)$ 是方程(1.3)的非平凡解，若存在 $x\left(t\right)\in C^1\left(\left[0,1\right];R\right)$ ，使得 $x\left(0\right)=x\left(1\right)=0$ ； $\frac{f\left(t,u,v\right)}{u}\le 0\left(u\ne 0\right)$ ，且

${\displaystyle {\int }_0^1\left\{\left[4C_2{C}_{1}p\left(t\right)q\left(t\right)+C_3\left(C_1-C_2\right)r^2\left(t\right)\right]x^2-C_3{C}_1{\left[2C_{2}p\left(t\right)x^{\prime }-r\left(t\right)x\right]}^2\right\}\text{d}t}>0,$

则 $y\left(t\right)$ 在 $\left[0,1\right]$ 上至少有一个零点。

证明 假设 $y\left(t\right)$ 在 $\left[0,1\right]$ 上没有零点，即 $y\left(t\right)\ne 0,t\in \left[0,1\right]$ ，则不等式(2.1)成立。对(2.1)式的两边从0到1积分得

$\begin{array}{l}{\displaystyle {\int }_0^1{\left[-\frac{x^{2}p\left(t\right)\varphi \left(y\right)k\left(y^{\prime }\right)}{y}\right]}^{\prime }\text{d}t}\\ \ge {\displaystyle {\int }_0^1\{{\left[\sqrt{\frac{p\left(t\right)\varphi \left(y\right)}{C_3}}\frac{k\left(y^{\prime }\right)x}{y}+\sqrt{\frac{C_3}{p\left(t\right)\varphi \left(y\right)}}\frac{r\left(t\right)x}{2}-\sqrt{C_{3}p\left(t\right)\varphi \left(y\right)}{x}^{\prime }\right]}^2}\\ -\frac{C_3}{4C_{2}p\left(t\right)}\left[2C_{2}p\left(t\right)x^{\prime }-r\left(t\right)x\right]+\frac{1}{4C_2{C}_{1}p\left(t\right)}[4C_2{C}_{1}p\left(t\right)q\left(t\right)\\ +C_3\left(C_1-C_2\right)r^2\left(t\right)]x^2-\frac{f\left(t,y,y^{\prime }\right)x^2}{y}\}\text{d}t.\end{array}$

由 $x\left(0\right)=x\left(1\right)=0$ ，有

${\displaystyle {\int }_0^1{\left[-\frac{x^{2}p\left(t\right)\varphi \left(y\right)k\left(y^{\prime }\right)}{y}\right]}^{\prime }\text{d}t}={\left[-\frac{x^{2}p\left(t\right)\varphi \left(y\right)k\left(y^{\prime }\right)}{y}\right]}_0^1=0.$

于是

${\displaystyle {\int }_0^1\left\{\left[4C_2{C}_{1}p\left(t\right)q\left(t\right)+C_3\left(C_1-C_2\right)r^2\left(t\right)\right]x^2-C_3{C}_1{\left[2C_{2}p\left(t\right)x^{\prime }-r\left(t\right)x\right]}^2\right\}\text{d}t}\le 0,$

与条件矛盾，故 $y\left(t\right)$ 在 $\left[0,1\right]$ 上至少有一个零点。

推论1 设 $y\left(t\right)$ 是方程(1.3)的非平凡解，若存在 $x\left(t\right)\in C^1\left(\left[0,1\right];R\right)$ ，使得 $x\left(0\right)=x\left(1\right)=0$ ； $\frac{f\left(t,u,v\right)}{u}\le 0\left(u\ne 0\right)$ ；又

$\left[4C_2{C}_{1}p\left(t\right)q\left(t\right)+C_3\left(C_1-C_2\right)r^2\left(t\right)\right]x^2\ge C_3{C}_1{\left[2C_{2}p\left(t\right)x^{\prime }-r\left(t\right)x\right]}^2$ ， $t\in \left[0,1\right]$ ，

且等号在[0,1]的任意闭子区间上不恒成立，则 $y\left(t\right)$ 在 $\left[0,1\right]$ 上至少有一个零点。

定理2 设 $y\left(t\right)$ 是方程(1.3)的非平凡解，若存在 $x\left(t\right)\in C^1\left(\left[0,1\right];R\right)$ ，使得 $x\left(0\right)=x\left(1\right)=0$ ；

$\frac{r\left(t\right)k\left(v\right)-f\left(t,u,v\right)}{u}\ge 0\left(u\ne 0\right)$ ；且

${\displaystyle {\int }_0^1\left[q\left(t\right)x^2-C_2{C}_{3}p\left(t\right){x^{\prime }}^2\right]\text{d}t}>0.$

则 $y\left(t\right)$ 在 $\left[0,1\right]$ 上至少有一个零点。

证明 假设 $y\left(t\right)$ 在 $\left[0,1\right]$ 上没有零点，即 $y\left(t\right)\ne 0,t\in \left[0,1\right]$ ，则不等式(2.2)成立。对(2.2)式的两边从0到1积分得

$\begin{array}{c}{\displaystyle {\int }_0^1{\left(-\frac{x^{2}p\left(t\right)\varphi \left(y\right)k\left(y^{\prime }\right)}{y}\right)}^{\prime }\text{d}t}\ge {\displaystyle {\int }_0^1\frac{p\left(t\right)\varphi \left(y\right)}{C_3}{\left(C_3{x}^{\prime }-\frac{k\left(y^{\prime }\right)}{y}x\right)}^2\text{d}t}\\ +{\displaystyle {\int }_0^1\left[q\left(t\right)x^2-C_2{C}_{3}p\left(t\right){x^{\prime }}^2\right]\text{d}t}\\ +{\displaystyle {\int }_0^1\frac{r\left(t\right)k\left(y^{\prime }\right)-f\left(t,y,y^{\prime }\right)}{y}{x}^2\text{d}t}.\end{array}$

由 $x\left(0\right)=x\left(1\right)=0$ ，有

${\displaystyle {\int }_0^1{\left(-\frac{x^{2}p\left(t\right)\varphi \left(y\right)k\left(y^{\prime }\right)}{y}\right)}^{\prime }\text{d}t}={\left(-\frac{x^{2}p\left(t\right)\varphi \left(y\right)k\left(y^{\prime }\right)}{y}\right)}_0^1=0.$

于是

${\displaystyle {\int }_0^1\left[q\left(t\right)x^2-C_2{C}_{3}p\left(t\right){x^{\prime }}^2\right]\text{d}t}\le 0,$

与条件矛盾，故 $y\left(t\right)$ 在 $\left[0,1\right]$ 上至少有一个零点。

推论2 设 $y\left(t\right)$ 是方程(1.3)的非平凡解，若存在 $x\left(t\right)\in C^1\left(\left[0,1\right];R\right)$ ，使得 $x\left(0\right)=x\left(1\right)=0$ ， $\frac{r\left(t\right)k\left(v\right)-f\left(t,u,v\right)}{u}\ge 0\left(\forall u\ne 0\right)$ ，又 $q\left(t\right)x^2\ge p\left(t\right)C_2{C}_3{x^{\prime }}^2$ ， $t\in \left[0,1\right]$ ，且等号在[0,1]的任意闭子区间上不恒成立，则 $y\left(t\right)$ 在 $\left[0,1\right]$ 上至少有一个零点。

定理3 设 $y\left(t\right)$ 是方程(1.3)的非平凡解，若存在 $x\left(t\right)\in C^1\left(\left[0,1\right];R\right)$ ，使得 $x\left(0\right)=x\left(1\right)=0$ ；

$\frac{f\left(t,u,v\right)}{u}\le 0\left(u\ne 0\right)$ ，且

${\displaystyle {\int }_0^1\left[Q\left(t\right)x^2-C_2{C}_{3}p\left(t\right)\Phi \left(t\right){\left(x^{\prime }+\frac{1}{2}x\bar{R}\left(t\right)\right)}^2\right]\text{d}t}>0,$

则 $y\left(t\right)$ 在 $\left[0,1\right]$ 上至少有一个零点。

证明 假设 $y\left(t\right)$ 在 $\left[0,1\right]$ 上没有零点，即 $y\left(t\right)\ne 0,t\in \left[0,1\right]$ ，则不等式(2.3)成立。对(2.3)式的两边从0到1积分得

$\begin{array}{c}{\displaystyle {\int }_0^1{\left[-x^{2}W\left(t\right)\right]}^{\prime }\text{d}t}\ge {\displaystyle {\int }_0^1{C}_2{C}_{3}p\left(t\right)\Phi \left(t\right){\left(\frac{W\left(t\right)}{C_2{C}_{3}p\left(t\right)\Phi \left(t\right)}x-x^{\prime }-\frac{1}{2}\bar{R}\left(t\right)x\right)}^2\text{d}t}\\ +{\displaystyle {\int }_0^1\left[Q\left(t\right)x^2-C_2{C}_{3}p\left(t\right)\Phi \left(t\right){\left(x^{\prime }+\frac{1}{2}\bar{R}\left(t\right)x\right)}^2\right]\text{d}t}-{\displaystyle {\int }_0^1\frac{f\left(t,y,y^{\prime }\right)}{y}\Phi \left(t\right)x^2\text{d}t}.\end{array}$

由 $x\left(0\right)=x\left(1\right)=0$ ，有

${\displaystyle {\int }_0^1{\left[-x^{2}W\left(t\right)\right]}^{\prime }}={\left[-x^{2}W\left(t\right)\right]}_0^1=0.$

于是

${\displaystyle {\int }_0^1\left[Q\left(t\right)x^2-C_2{C}_{3}p\left(t\right)\Phi \left(t\right){\left(x^{\prime }+\frac{1}{2}\bar{R}\left(t\right)x\right)}^2\right]\text{d}t}\le 0,$

与条件矛盾，故 $y\left(t\right)$ 在 $\left[0,1\right]$ 上至少有一个零点。

推论3 设 $y\left(t\right)$ 是方程(1.3)的非平凡解，若存在 $x\left(t\right)\in C^1\left(\left[0,1\right];R\right)$ ，使得 $x\left(0\right)=x\left(1\right)=0$ ； $\frac{f\left(t,u,v\right)}{u}\le 0\left(u\ne 0\right)$ ；又在 $\left[0,1\right]$ 上，

$Q_2\left(t\right)x^2\ge C_2{C}_{3}p\left(t\right)\Phi \left(t\right){\left(x^{\prime }+\frac{1}{2}x{r}_2\left(t\right)\right)}^2,$

但不恒相等，则 $y\left(t\right)$ 在 $\left[0,1\right]$ 上至少有一个零点。

4. 实例

例1 考虑方程：

${\left[\left(\text{1}+{\sin }^2\text{π}t\right)\frac{y^{\prime }}{1+\alpha {y^{\prime }}^2}\right]}^{\prime }+4\text{π}\sin \text{π}t\cos \text{π}t\frac{y^{\prime }}{1+\alpha {y^{\prime }}^2}+q\left(t\right)y+t^{2}y{y^{\prime }}^2=0$ (4.1)

其中 $y\in R$ ， $t\in \left[0,1\right]$ ， $\alpha \ge \text{0}$ 为常数， $q\in C\left(\left[0,1\right];\left[0,+\infty \right)\right)$ ，满足 $q\left(t\right)>\frac{4{\text{π}}^2}{{\sin }^2\text{π}t},t\in \left(0,1\right)$ 。

记 $p\left(t\right)=1+{\sin }^2\text{π}t$ ， $\varphi \left(y\right)=1$ ， $k\left(v\right)=\frac{v}{1+\alpha v^2}$ ， $r\left(t\right)=4\text{π}\sin \text{π}t\cos \text{π}t$ ， $f\left(t,u,v\right)=-t^{2}u{v}^2$ ，则 $f\in C\left(\left[0,1\right]\times R\times R;R\right)$ ， $p\in C^1\left(\left[0,1\right];R_{+}\right)$ ， $r\in C\left(\left[0,1\right];R\right)$ ， $k,\varphi \in C^1\left(R;R\right)$ ，且

$\frac{f\left(t,u,v\right)}{u}=-t^2{v}^2\le 0\left(u\ne 0\right).$

取 $C_1=C_2=C_3=1$ ，则条件(A1)、(A2)满足。取 $x\left(t\right)={\sin }^2\text{π}t$ ，则 $x\left(0\right)=x\left(1\right)=0$ 。

对 $t\in \left[0,1\right]$ ，有

$\begin{array}{l}\left[4C_2{C}_{1}p\left(t\right)q\left(t\right)+C_3\left(C_1-C_2\right)r^2\left(t\right)\right]x^2-C_3{C}_1{\left[2C_{2}p\left(t\right)x^{\prime }-r\left(t\right)x\right]}^2\\ =4q\left(t\right)\left(1+{\sin }^2\text{π}t\right){\sin }^4\text{π}t-{\left[4\text{π}\left(1+{\sin }^2\text{π}t\right)\sin \text{π}t\cos \text{π}t-4\text{π}\sin \text{π}t\cos \text{π}t{\sin }^2\text{π}t\right]}^2\\ =4{\sin }^2\text{π}t\left[q\left(t\right)\left(1+{\sin }^2\text{π}t\right){\sin }^2\text{π}t-4{\text{π}}^2{\cos }^2\text{π}t\right]\\ \ge 4{\sin }^2\text{π}t\left[q\left(t\right){\sin }^2\text{π}t-4{\text{π}}^2\right]\ge 0,\end{array}$

且等号当且仅当 $t=0,1$ 时成立。由推论1知，方程(4.1)的非平凡解 $y\left(t\right)$ 在 $\left[0,1\right]$ 至少有一个零点。

例2 考虑以下方程：

${\left(\frac{\text{2}+{\cos }^2\text{π}t}{1+{\cos }^2\text{π}t}\cdot \frac{1+y^2}{2+y^2}\cdot \frac{{y^{\prime }}^{\text{2}}}{1+\alpha {y^{\prime }}^2}\right)}^{\prime }+\frac{t^2{y^{\prime }}^{\text{2}}}{1+\alpha {y^{\prime }}^2}+q\left(t\right)y+\frac{y^3-t^2{y^{\prime }}^2}{1+\alpha {y^{\prime }}^2}=0$ (4.2)

其中 $y\in R$ ， $t\in \left[0,1\right]$ ， $\alpha \ge \text{0}$ 为常数。 $q\in C\left(\left[0,1\right];\left[0,+\infty \right)\right)$ ，满足 $q\left(t\right)>\frac{3{\text{π}}^2}{{\sin }^2\text{π}t},t\in \left(0,1\right)$ 。

记 $p\left(t\right)=\frac{\text{2}+{\cos }^2\text{π}t}{1+{\cos }^2\text{π}t}$ ， $\varphi \left(y\right)=\frac{1+y^2}{2+y^2}$ ， $k\left(v\right)=\frac{v^{\text{2}}}{1+\alpha v^2}$ ， $r\left(t\right)=t^2$ ， $f\left(t,u,v\right)=-\frac{u^3-t^2{v}^2}{1+a{v}^2}$ ，则 $f\in C\left(\left[0,1\right]\times R\times R;R\right)$ ， $p\in C^1\left(\left[0,1\right];R_{+}\right)$ ， $r\in C\left(\left[0,1\right];R\right)$ ， $k,\varphi \in C^1\left(R;R\right)$ ，且 $\frac{1}{2}\le \varphi \left(y\right)=\frac{1+y^2}{2+y^2}\le 1$ ， $\frac{r\left(t\right)k\left(v\right)-f\left(t,u,v\right)}{u}=\frac{u^2}{1+\alpha v^2}\ge 0\left(u\ne 0\right)$ 。

取 $C_1=\frac{1}{2},C_2=C_3=1$ ，则条件(A1)、(A2)满足。取 $x\left(t\right)=\sin \text{π}t$ ，则 $x\left(0\right)=x\left(1\right)=0$ ，且

$\begin{array}{l}q\left(t\right)x^2-p\left(t\right)C_2{C}_3{x^{\prime }}^2\\ =q\left(t\right){\sin }^2\text{π}t-\left(\frac{\text{2}+{\cos }^2\text{π}t}{1+{\cos }^2\text{π}t}\right){\text{π}}^2{\cos }^2\text{π}t\\ \ge q\left(t\right){\sin }^2\text{π}t-3{\text{π}}^2\ge \text{0}\end{array}$

且等号当且仅当 $t=0,1$ 时成立，由推论2知，方程(4.2)的非平凡解 $y\left(t\right)$ 在 $\left[0,1\right]$ 至少有一个零点。

例3 考虑方程：

${\left[\left(\text{1}+{\sin }^2\text{π}t\right)\frac{y^{\prime }}{1+\alpha {y^{\prime }}^2}\right]}^{\prime }-\text{2π}\sin \text{π}t\cos \text{π}t\frac{y^{\prime }}{1+\alpha {y^{\prime }}^2}+q\left(t\right)y+t^{2}y{y^{\prime }}^2=0,$ (4.3)

其中 $y\in R$ ， $t\in \left[0,1\right]$ ， $\alpha \ge \text{0}$ 为常数， $q\in C\left(\left[0,1\right];\left[0,+\infty \right)\right)$ ，满足

$q\left(t\right)\ge {\text{π}}^2\left(4+{\cot }^2\text{π}t\right),t\in \left(0,1\right).$

记 $p\left(t\right)=1+{\sin }^2\text{π}t$ ， $\varphi \left(y\right)=1$ ， $k\left(v\right)=\frac{v}{1+\alpha v^2}$ ， $r\left(t\right)=-2\text{π}\sin \text{π}t\cos \text{π}t$ ， $f\left(t,u,v\right)=-t^{2}uv$ ，则 $f\in C\left(\left[0,1\right]\times R\times R;R\right)$ ， $p\in C^1\left(\left[0,1\right];R_{+}\right)$ ， $r\in C\left(\left[0,1\right];R\right)$ ， $k,\varphi \in C^1\left(R;R\right)$ ，且

$\frac{f\left(t,u,v\right)}{u}=-t^2{v}^2\le 0,u\ne 0.$

取 $C_1=C_2=C_3=1$ ，则条件(A1)、(A2)成立。取 $x\left(t\right)=\sin \text{π}t$ ，则 $x\left(0\right)=x\left(1\right)=0$ 。

取 $R\left(t\right)=-\frac{1}{t},\Phi \left(t\right)=t^2$ ，则

$\begin{array}{c}Q\left(t\right)=\Phi \left(t\right)\left[q\left(t\right)-\frac{C_3\left(C_2-C_1\right)}{4C_1{C}_2}\frac{r^2\left(t\right)}{p\left(t\right)}-\frac{r\left(t\right)}{C_2}R\left(t\right)+\frac{p\left(t\right)}{C_2{C}_3}{R}^2\left(t\right)-{\left(p\left(t\right)R\left(t\right)\right)}^{\prime }\right]\\ \ge t^2\left[{\text{π}}^2\left(4+{\cot }^2\text{π}t\right)-\frac{\text{2π}\sin \text{π}t\cos \text{π}t}{t}+\frac{1+{\sin }^2\text{π}t}{t^2}-{\left(\frac{1+{\sin }^2\text{π}t}{-t}\right)}^{\prime }\right]\\ =t^2{\text{π}}^2\left(4+{\cot }^2\text{π}t\right)\end{array}$

$\bar{R}\left(t\right)=\frac{2R\left(t\right)}{C_2{C}_3}+\frac{{\Phi }^{\prime }\left(t\right)}{\Phi \left(t\right)}-\frac{r\left(t\right)}{C_{2}p\left(t\right)}=-\frac{2}{t}+\frac{2t}{t^2}-\frac{-2\text{π}\sin \text{π}t\cos \text{π}t}{1+{\sin }^2\text{π}t}=\frac{2\text{π}\sin \text{π}t\cos \text{π}t}{1+{\sin }^2\text{π}t}$

从而对 $t\in \left(0,1\right)$ ，

$\begin{array}{l}Q\left(t\right)x^2-C_2{C}_{3}p\left(t\right)\Phi \left(t\right){\left[x^{\prime }+\frac{1}{2}x\bar{R}\left(t\right)\right]}^2\\ \ge t^2{\text{π}}^2\left(4+{\cot }^2\text{π}t\right){\sin }^2\text{π}t-\left(1+{\sin }^2\text{π}t\right)t^2{\left(\text{π}\cos \text{π}t+\frac{\sin \text{π}t}{2}\cdot \frac{2\pi \sin \text{π}t\cos \text{π}t}{1+{\sin }^2\text{π}t}\right)}^2\\ =t^2{\text{π}}^2\left(4+{\cot }^2\text{π}t\right){\sin }^2\text{π}t-\left(1+{\sin }^2\text{π}t\right)t^2\left[{\text{π}}^2{\cos }^2\text{π}t+\frac{2{\pi }^2{\sin }^2\text{π}t{\cos }^2\text{π}t}{1+{\sin }^2\text{π}t}+\frac{{\text{π}}^2{\sin }^4\text{π}t{\cos }^2\text{π}t}{{\left(1+{\sin }^2\text{π}t\right)}^2}\right]\\ =t^2{\text{π}}^2{\sin }^2\text{π}t\left\{\left(4+{\cot }^2\text{π}t\right)-\left(1+{\sin }^2\text{π}t\right)\left[{\cot }^2\text{π}t+\frac{2{\cos }^2\text{π}t}{1+{\sin }^2\text{π}t}+\frac{{\sin }^2\text{π}t{\cos }^2\text{π}t}{{\left(1+{\sin }^2\text{π}t\right)}^2}\right]\right\}\\ \ge 2t^2{\text{π}}^2{\sin }^2\text{π}t\left\{3+{\cot }^2\text{π}t-\left[{\cot }^2\text{π}t+3\right]\right\}=0\end{array}$

而当 $t=0,1$ 时不等式仍成立，且等号在 $\left[0,1\right]$ 的任意子区间上不恒成立。由推论3知，方程(4.3)的非平凡解 $y\left(t\right)$ 在 $\left[0,1\right]$ 至少有一个零点。

致谢

感谢庄容坤教授对本文研究工作的建议和帮助！

基金项目

本文受如下基金项目资助：国家自然科学基金(No. 11601180)，广东省自然科学基金 (No. 2016A030310100)，国家级大学生创新训练项目(No. 20181057005)。

NOTES

^*通讯作者。