1. 引言
屈曲梁结构在军事、航空航天、土木、机械等工程中有广泛的应用,拱形结构当受到动态负荷时,会展示出丰富的动力学现象,包括次谐波、超谐振荡、极限环、混沌运动等 [1] [2]。1983年,Moon [3] [4] 等研究了非线性边界条件下的梁受到周期载荷后的混沌运动。Suire [5] 用数值方法研究了大扰度粘弹性梁的周期和混沌。冯志华,胡海岩研究了内共振条件下直线运动梁的动力稳定性,基于凯恩方程建立非线性动力学方程,得出非线性振动的Hopf分岔以及极限环。Danida [6]、Anantha [7]、Neukirch [8] 等研究了弹性屈曲梁的周期解和混沌动力学行为。张等 [9] [10] 研究了两端简支的非线性弹性梁受周期载荷作用后,发生次谐分岔和混沌运动的条件。Pinto [11] [12] 等分析了弹性屈曲梁在强迫力作用下出现马蹄混沌行为。
本文研究一类轴向载荷作用下梁的次谐分岔和混沌行为,对梁的单模态方程,应用Melnikov方法,得到了系统发生次谐分岔和超次谐分岔的参数范围,及混沌区域和非混沌区域的分界线。
2. 问题描述
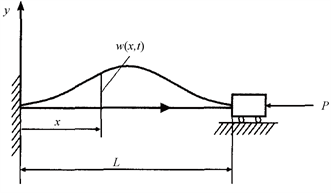
Figure 1. A buckled beam at axial motion
图1. 屈曲梁结构模型
如图1所示,考虑梁的长度为L,横截面积为A,横截转动惯量为J,材料的弹性模量为E,轴向力为P。假定梁的横截面是均匀的,材质均相同.轴向位移采用u表示,横向位移采用w表示,u和w是空间坐标x的函数,文献 [11] 得到弯曲梁的运动方程为
(1)
边界条件为
和
时,
,
利用伽辽金法,单模态的运动方程为
(2)
这里考虑
的情况,令
,
,
,则方程(2)变成
(3)
当
时,系统(3)的未扰动系统为
(4)
(4)是Hamiltonian系统,其Hamiltonian量为
(5)
3. 系统的次谐分岔与混沌
的混沌行为
当
时,利用如下变换
,
(6)
将(6)代入(3)式,得到
(7)
其中
,
,
。当
时,未扰动系统为
(8)
其Hamilton量为
(9)
该系统有三个平衡点,通过定性分析可知,
为(8)的中点,
和
是鞍点。当
时,存在两条连接
的异宿轨道,形成一个异宿环,如图2所示。
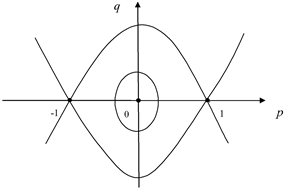
Figure 2. The phase portrait of system (8)
图2. 系统(8)的相图
该异宿轨道的参数表达式为
(10)
以
为参数的周期轨道为
(11)
其中sn,dn,cn为Jacobian椭圆函数,k为椭圆函数的模,
,k满足关系式
,定义轨道的周期为
,
是第一类完全椭圆积分。
下面计算系统(7)沿着异宿轨道的Melnikov函数
(12)
其中
,
由(12)可知,当参数
,
满足
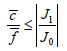 (13)
(13)
即参数
满足参数条件
存在零点,系统发生混沌。取不同的
值,比如
,得到系统发生混沌的临界曲线,如图3所示。在曲线下方是发生混沌的区域,在曲线上方是非混沌区域。
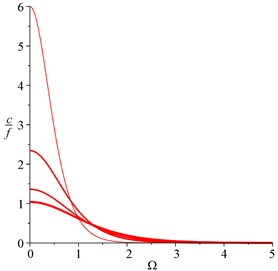
Figure 3. The critical curves for chaotic motions
图3. 系统发生混沌的临界曲线
4. 通向混沌的道路
对于任给的一对互素的正整数
,存在唯一的k,满足
,沿这个周期为
的轨道计算次谐波Melnikov函数得
(14)
其中
(15)
(16)
,
为第二类椭圆积分。
当参数满足条件
(17)
系统发生奇数阶次谐分岔。
5. 数值模拟
对系统(2)使用龙格库塔法做数值模拟来验证屈曲梁是否存在混沌现象。根据前面理论的分析来选取参数
,
,
,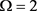 ,
,初始点选取为
,
,初始点选取为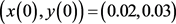 ,相图和时间历程图如图4所示。再令参数
,其它参数值不变,得到系统相图和时间历程图如图5所示。
,相图和时间历程图如图4所示。再令参数
,其它参数值不变,得到系统相图和时间历程图如图5所示。
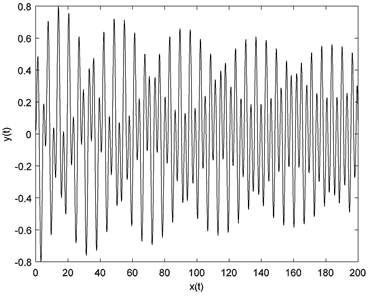
Figure 4. The phase portrait of system (2) for
图4. 当
时,系统的相轨迹图和时间历程图

Figure 5. The phase portrait of system (2) for
图5. 当
时,系统的相轨迹图和时间历程图
6. 结论
研究了受轴向载荷和附加载荷弹性屈曲梁的次谐分岔和混沌行为。利用Melnikov方法,给出了屈曲梁同宿轨道Melnikov函数和次谐Melnikov函数的表达式,得到系统出现次谐分岔和超次谐分岔的参数条件,给出系统混沌区域和非混沌区域的分界曲线。根据参数的取值范围做数值模拟,结果验证了理论分析。
基金项目
本论文受山东省自然科学基金资助(ZR2018MA002)和2018大学生创新创业项目资助(51819220)。
参考文献