考虑平衡负荷的混合遗传模拟退火柔性车间调度的研究

Research on Flexible Genetic Shop Scheduling with Mixed Genetic Simulated Annealing Considering Balanced Load

摘要: 本文针对柔性车间调度问题，提出一种混合遗传模拟退火算法，该算法采用遗传算法解决排序和全局搜索问题，使用模拟退火进行局部搜索，在求解过程中根据机器负载情况合理的对机器进行分配，并通过实例测试，验证了算法的有效性。

Abstract: In this paper, a hybrid genetic simulated annealing algorithm is proposed for flexible shop scheduling problem. The algorithm uses genetic algorithm to solve the problem of sorting and global search. It uses simulated annealing to perform local search. In the process of solving, the machine is allocated according to the load condition of the machine. The effectiveness of the algorithm is verified by an example test.

1. 引言

柔性车间调度问题 [1] (Flexible Job Shop Scheduling Problem，简称FJSSP)是Bruker和Schlie在1990年首次提出的。与经典车间作业调度相比较，柔性作业车间调度突破了资源唯一性的限制，增加了作业调度的灵活性，从而更适合智能化车间的生产要求。但是，柔性车间调度问题是一个更为复杂的NP问题，因此，研究FJSSP具有重要的应用价值和意义。

目前对柔性作业车间调度的主要研究方法为粒子群算法 [2] [3] 、遗传算法 [4] [5] 、蚁群算法 [6] 、邻域搜索算法 [7] 等算法，通过这些算法的迭代实现柔性作业车间调度方案的优化。黄学文 [8] 等人提出的基于OR子图和子路径的工艺路径调度算法通过遗传较好的实现了可行解；赵卫 [9] 在遗传算法种群更新过程中引入模拟退火机制，提高了种群更新迭代中多样性、加快了收敛、克服了早熟的缺陷，提高了调度的效率。这些学者研究车间调度算法及其优化都只是针对柔性车间中某一道工序指定一台加工设备而言，不能应用于一道工序指定多台加工设备的分配和调度问题。为了更好的解决此问题，陈成 [10] 等人使用蚁群遗传混合算法解决了机器分配及工序排序，能够有效的解决一道工序可由多台设备加工的分配和调度问题，但是使用轮盘赌法增加了局部最优值的不确定性。

因此，面对智能化车间调度系统，考虑到柔性车间中每台加工设备的性能、型号、用途等不尽相同，但每个加工设备的通用性强，加工工件的种类和工序的数量较多的前提，使用传统的一道工序必须由指定一台设备加工的调度方案已经不能够适应生产需求的因素，本文从两个方向对FJSSP进行设计和优化，1) 对车间调度本身的算法进行了负荷平衡的改进和优化，有效的解决了机器合理的选择与分配问题。2) 基于优化的混合遗传算法和模拟退火算法，利用遗传算法隐式并行处理能力和强鲁棒性的特点寻找全局最优，利用模拟退火算法在大规模的解空间中寻找局部最优，提高了车间调度的效率，并通过车间作业调度测试案例仿真验证算法的有效性。

2. 作业车间调度问题

2.1. 作业车间调度问题表述及其约束条件

在流水车间中，对于n个待加工工件进行加工，每个工件又具有一个或者多个加工工序，每个工件依照加工流程中工序顺序进行排产，考虑到柔性车间中所有的机器的性能，型号，用途等不尽相同，机器加工工件的种类、同一工件的工序、同一工序的时间也都不尽相同。因此考虑调度问题是要讲各个工序分配到各台机器上，并合理地安排工序的加工次序和时间，从而尽可能满足性能指标，这增加了问题的复杂性和求解难度，但更加符合实际的多样化生产环境。

FJSSP可以描述为：

1) 工件集 $J=\left\{J_{\text{1}},J_2,\cdots ,J_n\right\}$ ，J_i为第i个工件， $\text{1}\le i\le n$ ；

2) 机器集 $M=\left\{M_1,M_2,\cdots ,M_m\right\}$ ，M_j为第j号机器， $\text{1}\le j\le m$ ；

3) 工序集 $O=\left\{O_1,O_2,\cdots ,O_n\right\}$ ，O_i为第i个工件的工序， $\text{1}\le i\le n$ ；

4) 工序子集 $O_i=\left\{O_{i1},O_{i2},\cdots ,O_{im}\right\}$ ，O_ik为第i个工件的第k道工序使用的机器号， $1\le k\le m$ ； $O_{ik}=1$ 表示工件J_i的第k道工序由机器号加工， $1\le k\le m$ ；

5) 每道工序加工的使用时间 $T_i=\left\{T_{i1},T_{i2},\cdots ,T_{in}\right\}$ ，T_ik为第i个工件的第k道工序所使用的机器号完成所消耗的时间， $\text{1}\le k\le n$ 。

FJSSP需要满足以下的约束条件：

1) 每个加工机器彼此互相独立，不考虑机器故障带来的影响，并且所有的机器都是从(t = 0)时刻开始工作。

2) 所有的工件彼此互相独立，任一工件的加工不会影响其他工件的加工，所有工件均可在开始时刻加工。

3) 加工过程中不能突然改变工件工艺，所有的工件的工序在排产以前就已经确定。

4) 所有机器的加工每件的时间由机器本身的加工效率和工艺决定和确定，加工过程中不会对任何工件的任一工序的时间有所改变。

5) 每台设备每个时刻只能加工一个工件的一个工艺，同一工艺不能在多台机器上加工，一道工艺在某台加工设备上一旦开始加工，直至该工艺加工完成，中间不能中断。

6) 加工机器严格遵守工件工序的加工时间。

本文研究最小化最大完工时间调度目标的FJSSP。只考虑工件在加工设备上的加工时间，不考虑加工设备的调整时间以及工件在各个加工设备之间的运输时间。因此，一个工件的完工时间等于该工件的各个工艺在相应加工设备上的加工时间和等待时间之和。

目标函数是最小化最大时间，即：

$C=\min \left(\underset{1\le j\le n}{\max }\left(\underset{1\le j\le m}{\max }{e}_j\right)\right)$ (1)

其中的e_j表示为第j号机器的完工时间。

2.2. 平衡负荷的设计

由于每道工序都可以由一台或多台设备加工，系统在为工件加工分配机器的时候往往并行机器需要合理分配加工任务，均衡设备负载，提高整体运作效率。通过计算每台机器负载均方差来反应当前机器的负载情况，负载均方差越小，该机器的负荷越小，越应优先分配加工任务。

假设调度系统正在分配工件J_i的第k道工序，参考工序集O_i可以确定由工序子集O_ik的k台机器来加工，设T_j为第j台机器当前加工总时长；T_total为所有机器加工总时长； $\bar{T}$ 为每台设备的平均加工时长；Nlb表示负载因子，Nlb越小表明该机器优先分配第i工件的第k道工序越合理。

构建平衡负荷数学模型如下：

$T_{\text{total}}={\displaystyle {\sum }_{j=1}^m{T}_j}$ (2)

$\bar{T}=\frac{T_{\text{total}}}{M}$ (3)

$Nlb=\sqrt{{\displaystyle {\sum }_{j=1}^k\left(T_j+T_{ij}-\bar{T}\right)}/M}$ (4)

3. 基于遗传和模拟退火的车间调度算法

遗传算法(Genetic Algorithm, GA)的主要思想基于达尔文进化论和孟德尔的遗传学，它结合了达尔文的适者生存和随机交换理论，是一种自然进化系统的计算模型，也是一种通用求解优化问题的搜索方法。遗传算法后期适应度趋向一致，优秀个体在产生后代时，优势不明显使得整个种群进化停滞。因此有必要对适应度进行适当的拉伸，当在温度较高的时候，适应度详尽的个体产生后代的概率相近，而温度下降的时候拉伸作用加强，使得适应度相近的个体适应度差异放大，从而使优秀个体优秀更显著。既有效的克服了遗传算法的早熟现象，同时又能有效的快速收敛得到全局最优解。

模拟退火算法(Simulated Annealing Algorithm, SA)是1982年由Kirkpatrick等人提出的一种模拟金属退火机理而建立的随机优化方法。模拟退火算法是局部搜索算法的扩展，它不同于局部搜索算法的支出是以一定的概率选择邻域中费用值大的状态，适用于解决大规模组合优化问题。

3.1. 编码

本文采用工件的整数排列的编码方法，即以工件为基本变量，工件号的排序作为编码，代表着染色体的基因组成。一个工件可以在染色体中出现多次，表示该工件的多个工序。比如有5个工件的染色体编码：“11223443355”其中1，2、3、4、5为工件号，分别重复出现了2、2、3、2、2次，这些也说明了其工序数量分别是2、2、3、2、2道，且每次出现的顺序代表的是工序顺序，编码中的9位的“3”是第二次出现，所以第9位代表的是工件3的第二道工序。该编码的优点在于工件工序变化不定的情况能够灵活适用。

3.2. 适应度函数设计

适应度函数决定了基因序列的好坏程度，适应度函数一般是目标函数的倒数，即优化的目标是适应度函数值尽量选择最小化最大时间最小的染色体序列，适应度函数值越大染色体越优质，反之亦反。目标函数公式为：

$F=\frac{1}{P_n}$ (5)

3.3. 选择操作

选择操作即从旧群体中以一定概率选择个体到新群体中，个体被选中的概率跟适应度的值有关，个体适应度值越大，被选中的概率越大。操作步骤如下：

1) 首先确定种群在下一代中的生存数目：

$N^{*}={\displaystyle {\sum }_{i=1}^N\lfloor N\ast F_i/{\displaystyle {\sum }_{i=1}^N{F}_i}\rfloor }$ ( $i=1,2,\cdots ,N$ ) (6)

N为种群的规模，F_i为第i个染色体的适应度值。

2) 根据二元锦标赛方式选择较好的个体，即每次从种群中随机选出两个个体进行对比，将适应度较高的个体保存到下一代中，重复这个过程直至下一代新种群的数量达到预期数量N^*。

$C_i^{*}=\{\begin{array}{l}{C}_i,F_i>F_{i+1}\\ C_{i+1},F_i<F_{i+1}\end{array}$ (7)

比较C_i和C_i+1两个个体的适应度值，保留适应度值大的个体进入下一代的种群中。

3.4. 交叉操作

种群的交叉操作是为了得到有益的新基因染色体。通过交叉操作让染色体有规律的基因进行交换从而得到两个新的染色体。这个过程要确保父代中的优良信息能够遗传到子代，尽量少的将不必要的遗传信息传给子代。本文采用一种工序编码的PBX算法(Position-based Crossover)的改进算法具体流程如下：

1) 在种群中随机选取两个P₁和P₂染色体作为父代染色体，并初始化基因个数与父代个数相同的C₁和C₂，作为下一代个体。

2) 首先随机划分工件集 $\left\{\text{1},\text{2},\cdots ,n\right\}$ 为一个非空子集set₁，set₂。 $se{t}_{\text{1}}\cap se{t}_{\text{2}}=\varnothing$ 。

3) 将P₁中存在的与set₁集合中相同的基因复制到C₁中，复制到C₁中的基因位置也与在P₁位置对应相同。

4) 将P₂中不存在于set₁集合中的元素按顺序复制到C₁的空缺位置中，如图1。

交叉概率的自适应调整，其公式为：

$P_c=\{\begin{array}{l}0.9-0.3\frac{F^{\prime }-F_{\text{avg}}}{F_{\max }-F_{\text{avg}}},F^{\prime }\ge F_{avg}\\ 0.9,F^{\prime }\le F_{\text{avg}}\end{array}$ (8)

公式中：P_c为交叉概率；F_max是群体中最大的适应度。F_avg为每一代群体的平均适应度值，F'为交叉后染色体的适应度值。

Figure 1. PBX cross graph

图1. PBX交叉图

3.5. 变异操作

变异操作是将个体染色体中的基因编码序列改变从而达到新的个体的操作。它能改善遗传算法的局部搜索能力，维持种群的多样性，防止“早熟”的发生。本文的变异方法使用随机选择位置置换的方法。随机选择两个变异的位置，互相交换即可，如图2。

Figure 2. Gene variation graph

图2. 基因变异图

变异操作使用自适应概率，公式为：

$P_m=\{\begin{array}{l}0.9-0.3\frac{F^{\prime }-F_{\text{avg}}}{F_{\max }-F_{\text{avg}}}\\ 0.9,F^{\prime }\le F_{\text{avg}}\end{array},F^{\prime }\ge F_{avg}$ (9)

其中F_avg为每一代群体的平均适应度值，F'为交叉后染色体的适应度值。

3.6. 模拟退火操作

本文中对模拟退火进行改进，将模拟退火结合遗传算法的交叉、变异操作，本算法既使收敛速度加快，又要维护种群的多样性，过程如图：

1) 初始化：初始温度为T(充分大)，终止温度T_min，初始化种群P，令当前状态为P_i，最优解 $P^{*}=P_i$ ，t = 0，设置循环计数器k，降温系数d，L表示Metropolis算法第次迭代时产生的变换个数；

2) 产生新状态S'，计算增量 $\Delta f^{\prime }=f\left({P^{\prime }}_i\right)-f\left(P_i\right)$ ；

3) 判断ΔC'，若 $\Delta C^{\prime }>0$ ，以概率 $\exp \left(-\Delta f^{\prime }/t\right)$ 接受P'为当前的状态，P'被接受则令P' = P，令t = t + 1；否则接受P'为当前的状态，计算增量 $\Delta C^{\prime }=C\left({P^{\prime }}_i\right)-C\left(P_i\right)$ 若 $\Delta C^{\prime }>0$ 则 $P^{*}=P^{\prime }$ ，令t = 0；

4) 判断是否 $t\ge L_k$ ，当前的状态是否无变化，如果是则结束循环；

5) 判断k是否终止，如果终止则令k = k + 1；转到步骤2，否则结束；

6) 重复以上操作直到对种群中的所有个体都完成了搜索。

3.7. 算法流程

步骤1：初始化种群大小、初始温度、交叉概率等模拟退火和遗传算法中需要的各种参数。

步骤2：随机产生初始种群。

Figure 3. Algorithm flow chart

图3. 算法流程图

步骤3：进行选择操作，计算个体适应度值、评价个体好坏，从中选择出较好的个体组成下一代种群。

步骤4：进行交叉操作，得到交叉个体进行模拟退火操作，根据P_c概率判断是否接受交叉操作所得到的新个体，然后再根据Metropolis准则判断是否接受，如果不能被接受，重复进行交叉操作直到出现可以被接受的个体之后进入下一步。

步骤5：进行变异操作，得到的变异个体进行模拟退火操作，根据P_m概率判断是否接受交叉操作所得到的新个体，然后再根据Metropolis准则判断是否接受，如果不能被接受，重复进行变异操作直到出现可以被接受的个体之后进入下一步。

步骤6：根据公式 $l_{t+1}=a\cdot l_t$ 对算法进行降温。

步骤7：判断是否满足终止条件，若满足条件输出最优个体，终止；若不满足条件返回到步骤3继续寻优直到满足条件为止。

算法流程如图3所示。

4. 仿真比较及分析

算法运行环境为Intel core i3、CPU主频2.4 GHz、4 GB内存、Windows 10操作系统，并采用Java语言编写。算法的主要参数：种群数取100，最大循环代数取200，初始温度为1000℃。

4.1. 仿真试验1

第一种算例是分别以FT06、FT10、FT20这三个调度问题作为测试基准 [11] ，将其他文献提供的算法进行实现和计算，每类问题中均进行了10次仿真计算平均值，将最优值与其他算法进行分析对比，这些算法包括GT-GA (Giffler-Thompson GA)、GP-GA (Generalized-Permutation GA)等。实验结果见表1。

Table 1. Comparison table of the results of experiment 1

表1. 实验一结果对比表

对于标准算例FT06问题，本算法能够快速收敛得到最优解，对于FT10与FT20问题也能得到次优解。我们从实验结果表一中得到本文中的混合遗传算法最优解相比较好或持平与其他算法。然而，基准问题只适用于工件工序确定的情况，即每台机器固化了的加工工序及加工时间，不涉及机器分配及负载问题。图4显示了FT06最优解Gantt图。

4.2. 仿真试验2

第二种算例的设计使用文献 [12] 中提出了一个模拟车间作业的算例，该算例中有6个工件在10台机器上加工，并且每个工件上有6道加工工序的实例，其加工时间如表2所示。

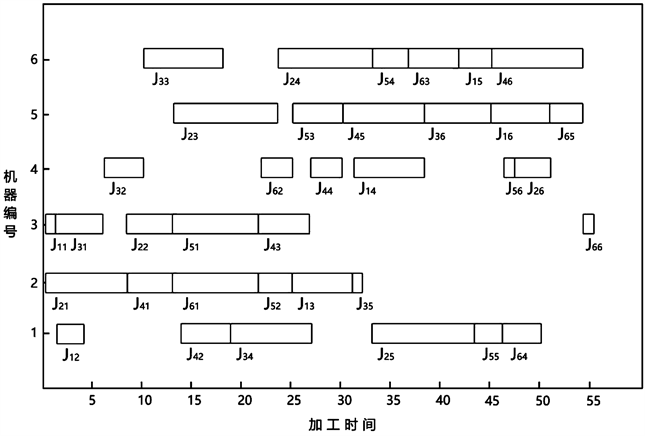
Figure 4. Optimal scheduling diagram of FT06 example

图4. FT06算例最优调度图

Table 2. Job shop scheduling example table

表2. 车间调度算例表

当算法程序运行时，在原有的决策基础上再对每台设备运行的负载情况进行考虑，有利于机器分配均匀，减少机器等待时间。由表3得出，使用相同算例，本文算法能够求解出更好的最优值，同时反映到机器上的负载平方差更小，更利于机器分配均衡。图5显示了本文算法求解的车间调度问题的最优Gantt图。

Figure 5. The optimal scheduling diagram of job shop scheduling example in experiment 2

图5. 实验二车间调度算例最优调度图

Table 3. Test and comparison results of Job Shop scheduling example table

表3. 车间调度算例表的测试对比结果

5. 结论

平衡负荷的生产柔性作业车间调度问题是对传统柔性作业车间调度问题的改良，它更接近于实际生产调度问题，针对该问题的特点，本文提出了一种基于混合遗传模拟退火算法的平衡负荷算法。即考虑一道工序由多台设备加工的可能性，结合SA与GA算法的同时提出了一种根据机器负载因子分配加工机器的方法。通过对基准算例和实际车间应用的算例进行模拟和仿真，对算法性能进行比较分析和评价，结果表明了算法的有效性和可行性。

在实际生产中，作业车间调度通常属于具有多种约束条件的多目标优化问题，为了将本文提出的算法应用于实际生产，还需进一步深入研究。