1. 引言
我国民航行业一直处于高速持续发展中。据统计:2018年旅客的运输量增长10.2%,起降架次增长8.2%,占据第二大航空运输系统的地位。行业的快速发展对自身的发展形成巨大压力,各繁忙机场都频繁出现大面积延误等情况,不利于行业的健康发展。高效的编排航班生产计划能够提高航空器的利用率,运载率以及航空公司的经济效益。数据显示:航班正常率提升0.1%,航空公司的盈利收入将增加45万以上 [1] 。采用新技术新优化方案,降低航班延误率,将产生巨大经济收益,同时也有助于提升航空公司品牌形象与影响力。国内外的航空企业都将非正常航班恢复作为研究重点,目前,对非正常航班的恢复算法和方案,国内外学者都有深入研究,但针对综合旅客成本,机组恢复和飞机调度的研究较少,本文将从这个角度进行研究。
在飞机恢复方面:Teodorovic等 [2] 提出以最小旅客航班延误总时间为目标函数,将航线网络模型看成具有边约束的网络流,利用用Benders分解算法进行求解。Stojkovic [3] 针对飞机路线和机组任务匹配进行研究,采用Dantzig-Wolf 算法求,产生新的优化航班时刻。在机组恢复方面:Guo Wei等 [4] 通过利用多商品流的分配理论,建立机组恢复的数学模型,利用分枝定界的启发式搜索算法对问题进行求解。Kohl等 [5] 提出将飞机路线恢复、机组恢复以及旅客行程恢复问题结合,建立以多种资源决定支持系统的数学模型,并设计了算法进行求解。Medard等 [6] 提出了航班网络的深度优化的搜索算法,利用算法生成周期航班任务列,并利用数据进行实证研究,数据表明算法能够对受扰机组进行优化调度。刘德刚 [7] 利用数学模型得到了飞机恢复方案,再利用另一算法得到机组恢复方案,比较机组恢复与飞机恢复法方案是否相匹配,如匹配,输出方案,得到航班恢复计划,如不匹配,修改方案。周志忠 [8] 整合了航班计划恢复模型、飞机恢复模型、机组人员恢复模型以及旅客行程恢复模型。利用了遗传算法对模型进行了求解。姚韵 [9] 将匈牙利法引入时空网络的模型研究,研究了航班任务置换的机理,论证了任务路径置换的成本关系,提出基于路径置换的分阶段优化算法,为飞机路线的恢复提出了新的求解思路。高强 [10] 在贪婪随机自适应搜索算法基础上,加入模拟退火算法来优化不正常航班恢复的调度问题。
2. 不正常航班恢复基本方案
不正常航班计划恢复问题是多约束多变量问题,受扰航班恢复是一个大规模整数规划实时求解的问题。航班受扰后,航空公司会对飞机资源、机组资源、旅客的行程安排等进行资源重组,生成一份临时性计划,使航班计划尽快恢复到正常,以便后续的航班计划的正常的执行。航空公司的不正常航班恢复问题可以分为以下四个子问题:1、航班、复问题:通过延误、取消、合并、备降航班来修复航班时刻表;2、飞机计划恢复问题:又称飞机路线恢复问题,飞机恢复主要策略有:机型替换,飞机交换,不同航空公司航班合并,使用备份飞机等。3、受扰机组的恢复问题:为修复后的航班时刻表指派具体机组。机组恢复的主要策略有:加机组或搭机、使用备份机组等。4、受扰航班的旅客行程的恢复问题:为受扰旅客安排新的行程,尽快将其运抵目的地。旅客是航空公司服务的对象,旅客行程恢复对航空公司的服务质量提升非常重要。
3. 不正常航班恢复问题建模
3.1. 航班恢复模型的参数分析
受扰航班的恢复面临两个困难:一是受扰航班延误的成本计算,二是航班恢复的时间随机性。通过已有的文献,本文将成本概括为:飞行延误成本,地面延误成本,飞机调配成本,旅客食宿成本,航空公司品牌形象损失。受扰航班的恢复是一个实时性问题。由于外界环境的影响是在随机的。因此模型中的成本为统计成本。
3.2. 模型建立
根据已有的文献,当飞机在运行过程中通常将飞机在空中等待时间转化为地面等待时间。对于m个延误航班
,F表示所有航班
,i表示本公司航班数量,
,S为分配给航空公司的所有时隙集合
,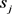 表示分配给本公司的时隙,
表示分配给本公司的时隙, ,根据上述分析,以航班延误恢复成本最小作为目标函数,建立模型:
,根据上述分析,以航班延误恢复成本最小作为目标函数,建立模型:
(1)
其中: 是当航班
指派到时隙
是当航班
指派到时隙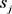 时,
时, :否则
:否则 ;
是该机型每小时的运营平均成本。
是航班
;
是该机型每小时的运营平均成本。
是航班 的每小时盈利损失,
,
是航班
的平均票价,
是航空公司每架航班的平均利润率,
航班预计要飞行的时间,
是航班
的每小时盈利损失,
,
是航班
的平均票价,
是航空公司每架航班的平均利润率,
航班预计要飞行的时间,
是航班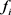 的旅客单位时间延误的经济损失,
的旅客单位时间延误的经济损失, ,
是每名旅客单位时间平均延误成本。
是时隙的最初时间。
是航班
初始时刻表要起飞时间。
表示航班延误的时间。
,
是每名旅客单位时间平均延误成本。
是时隙的最初时间。
是航班
初始时刻表要起飞时间。
表示航班延误的时间。
以最小旅客总延误时间为目标函数建立数学模型:
 (2)
(2)
其中: 是航班
的旅客人数。
是航班
的旅客人数。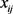 :当航班
指派到时隙
:当航班
指派到时隙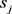 上时,
:否则为0。
是时隙的起始时间;
:是航班
初始时刻起飞时间。
上时,
:否则为0。
是时隙的起始时间;
:是航班
初始时刻起飞时间。
4. 模型求解
4.1. 模型的归一化处理
本中以飞机延误总成本和旅客延误总时间为目标函数建立多目标规划模型。两目标函数单位不统一,需进行量纲转化。通过变换,根据以往研究,引入目标函数权重系数
将多目标变换成线性加权的形式,
其中:
。
4.2. 基于遗传算法的求解
有关遗传算法的介绍,许多文献都有介绍 [11] [12] ,按照遗传算法的基本要求,本文利用该方法进行了求解,航班与分配的时隙是一一对应的关系,保证每个航班都被分配一个时隙。本文根据模型的特点与航班和时隙的关系选择二进制0-1编码,并通过产生随机数的方式选择变异和交叉的位置,加快计算的速度。具体如下:
1) 确定种群大小n,交叉概率
,变异概率
;
2) 初始化种群:产生n组可行解组成初始种群
;
3) 计算种群中个体的适应度值并进行选择操作;
4) 按照交叉概率
、变异概率
进行遗传操作;
5) 算法终止条件判断,如果满足终止条件,则输出最优解,算法结束,否则转步骤3。
在本模型中,种群即为航班与时隙的分配方案,使用随机化法生成初始种群,种群大小为100。遗传运算中,交叉概率 取值0.95,变异概率
取值0.05,在计算适应度时,使用TS算法来改进种群个体质量,使得找到最优解效率有所提升。适应度函数选取:
取值0.95,变异概率
取值0.05,在计算适应度时,使用TS算法来改进种群个体质量,使得找到最优解效率有所提升。适应度函数选取:
(3)
5. 案例分析
5.1. 案例参数
本文涉及到的机型按尾流等级分为重型(H)、中型(M)。双流机场由于流量控制的原因出现航班延误,其中在08:00~11:00时间段影响到国内某航空公司7个航班的正常执行,具体航班信息见表1。

Table 1. Basic information of affected flights
表1. 受影响航班基本信息
通过分析发现,将会有7个航班都会产生不同程度的延误。显然,这样的航班安排不利于航空公司的利益要求,同时也大大降低了航班正点率。对航空公司的不利影响大大加大。
运营成本匹配, 取值如表2所示:
取值如表2所示:
其中:航空公司平均利润率 可以取值为2.6%;时间-金钱系数
;每名旅客单位时间平均延误成本
可以取值为50元/小时;航空公司运行控制中心对本次不正常航班恢复的成本损失
可以取值为2.6%;时间-金钱系数
;每名旅客单位时间平均延误成本
可以取值为50元/小时;航空公司运行控制中心对本次不正常航班恢复的成本损失 、旅客总延误时间
、旅客总延误时间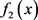 的重视程度分别为
。
的重视程度分别为
。
5.2. 案例计算结果
航班调整决策目标数值计算,具体结果如表3所示:
根据计算结果,做出分析如下表:由以上计算结果分析,运用遗传算法,成本损失目标函数在第12次迭代时达到最小值10378,旅客总延误时间目标函数在第12次迭代时达到最小值12607 min。具体结果如表4所示

Table 4. The result of reallocating slots
表4. 航班重新分配时隙的结果
从表3和表4中的计算结果可以看出,算法优化的原则是优先保障大型飞机、旅客人数多、票价高的航班,以及航程短、旅客人数少、票价较低的航班。最终计算结果中,成本损失由航班调整前的12004元减少到10378元,旅客延误总时间由航班调整前的13811 min减少到12607 min。由此可见,成本损失的减少比较明显,而旅客延误总时间较航班调整前增加287 min。导致这个结果的主要原因是成本损失与旅客总延误时间对决策者有着不同的权重,即受到公司的制度,不正常航班处理规定,以及公司利益目标的影响。
计算结果表明,本文所建立的基于多目标优化的受扰航班恢复模型,在一定的程度上能有效对成本因子以及延误时间进行综合分析。可根据子目标函数的权重进行调整,从而达到不同的航班调配策略。综合考虑建立的模型与算法运用,本模型更适用于航班量较大,分配的时隙比较集中的航空公司。对于短时间内不正常航班的调配具有显著作用。
6. 结论
本文对航班延误问题中涉及的航班延误成本和旅客总延误时间两大问题:进行了研究。通过分析建立了多目标优化数学模型并通过遗传算法对问题进行了求解。对案例进行分析发现建立的多目标不正常航班恢复模型,能有效对成本因子以及延误时间综合分析。根据子目标函数的权重达到不同的航班调配策略。能够有效地利用时隙资源,减少航空公司的损失,减少旅客总延误时间。在一定意义上,本模型是成功的。