1. 引言
定义D为一个区域,假设
为D内的一族亚纯函数,若对于
的任一函数序列
均可选出子序列
在D内按球面距离内闭一致收敛于一个亚纯函数,或者
,则称
在D内正规(详见 [1] - [7] )。
a是复平面
上的一个复数,f和g是区域D内的两个亚纯函数,如果
和
在D内有相同的零点,则称f和g在D内IM分担a;若
和
在D有相同的零点,且所有的零点重级也相等,则称f和g在D内CM分担a。
1996年,方明亮 [8] 提出了分担集合的概念。
f和g是区域D内的两个亚纯函数,
,S是一个由三个有限复数组成的集合。定义
,其中
。如果
,则称f和g分担集合S。
为区域D内的一族亚纯函数,我们称
在D内一点
正规,如果存在
的一个领域
,使
在
内正规。
1992年,Schwick [9] 最早研究与分担值相关的亚纯函数族的正规性,证明了
定理A 设
为D上的一族亚纯函数,
是三个不同的有限复数。若对任意的
,
,其中
中,
在D内正规。
2000年,庞学诚和Zalcman [10] 改进了Schwick [9] 的结果,证明了
定理B 设
为D上的一族亚纯函数,a,b,c和d是有穷复数,且
和
。若对任意的
,1)
;2)
,则
在D内正规。
如果
(定理A)替换成
,是否能得到相同的结论。在这个方面,在2007年,刘晓俊与庞学诚 [11] 证明了以下的结果。
定理C 设
为D上的一族亚纯函数,
是三个不同的有限复数。若对任意的
,
,其中
,则
在D内正规。
2002年,方明亮和Zalcman [12] 考虑了f和
分担一个值的情形,证明了
定理D 设
为D上的一族亚纯函数,a和b是两个非零有限复数,k是一个正整数。若对任意的
,1)
;2) f的零点重级均
,则
在D内正规。
如果我们把
(定理C)改为
,自然地,我们会问是否存在相关的正规定则。在这个方面,在2011年,张汉等人 [13] 证明了以下的结果。
定理E 设
为D上的一族亚纯函数,
,
是三个不同的有限复数,
是一个正整数,a为任意一个有限复数。若对任意的
,1)
;2)
的零点与极点重级均
。
2016年,徐焱与仇惠玲 [14] 考虑f与
分担两个集合的亚纯函数的正规性,证明了
定理F 设
为单位圆盘
上的一族亚纯函数,
,
,其中
都是有限复数且
。若对任意的
,1)
;2) 存在一个正整数M,若
,则
,则
在
内正规。
2014年,李效敏 [15] 等人考虑f和
分担集合的情形,证明了
定理G 设
为D上的一族亚纯函数,
是一个正整数,
和
都是由有限复数组成的集合。若对任意的
,1)
;2)
的零点重级均
,则
在D内正规。
本文推广了李效敏 [15] 等人的结果,证明了
定理1 设
为D上的一族亚纯函数,
和q是一个正整数,
和
都是由
有限复数组成的集合。若对任意的
,1)
;2)
的零点重级
均
,则
在D内正规。
以下的例子(张汉等人 [13] )说明定理1中关于零点重级的限制是必要的。
例 设
为定义在单位圆盘
上的亚纯函数族,其中
,
,
,
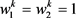 ,
和q是正整数。显然,对于
,有
,而
,
,
和q是正整数。显然,对于
,有
,而
,
根据Marty正规定则,可知
在
上不正规。
2. 引言
为了证明定理1,需要下列引理。
引理1 (Zalcman-Pang引理) [16] 设
为单位圆
内的一族亚纯函数,k和p均为正整数,如果对于
,
的零点重级
,极点重级
,且存在一个正数
,若
,必有
。那么,若
在单位圆内不正规,则对于每个
,
,存在
1) 函数列
;
2) 点列
;
3) 正数列
;
4) 实数r,
,
使得函数
在复平面
上按球面距离内闭一致收敛于一个非常数亚纯函数
,并且
的零点重级
,极点重级
,它的级至多为2,
。
引理2 [1] [17] [18] 设f为有穷级的超越亚纯函数,b是一个非零复数,k为正整数,则f或者
有无穷多个零点。
引理3 [19] 设f为有理函数,则f能取任意复数,至多有一个Picard例外值,并且f有且仅有一个亏值。
引理4 [20] 设
是一个正整数,f是复平面上的一个有穷级的亚纯函数,且
的零点个数是有限的,则f的极点个数是有限个。
3. 定理1的证明
证明:假设
在D内不正规,则存在一点
,使
在
处不正规则。由引理1,可知存在函数列
,点列
,正数列
,使得函数
(1)
(2)
在复平面
上按球面距离内闭一致收敛,其中
是一个非常数亚纯函数,
和
的级至多为2,且它们的零点重级均
。
下面我们分两种情形进行讨论。
情形1。存在
,使
,
或
,
,不失一般性,我们假设
。
令
。根据已知条件,可知
的零点重级至少为k。取
,使
在邻域
内是全纯的,否则,
在
上内闭一致收敛于全纯函数
。接下来我们证明
在
处不正规。因为
是一个非常数亚纯函数,所以
,则存在一点
,使
。根据Hurwitz定理,可知存在一个点列
且
,使
。当
时,
。故对任一
,存在一个正数
,使
。从而
矛盾。
如果
,也就是说
。根据条件,可得
,
则存在
,使得
,由此可知,若
,则
。假设
。
根据引理1,则存在正数列
;复数列
;子序列
;使
在
上按球面距离内闭一致收敛到非常数亚纯函数
,其中
的零点重级均
,级至多为2,且
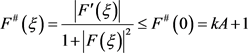 。
。
我们断言:
1) 在复平面
,
的零点个数是有限的;
2)
。
令
是
的l重零点。若
零点个数是无穷多个,可取
的
个互不相同的零点
。由于
,根据Hurwitz定理,可得存在
,使得
,也就是说,当
时,
。根据Hurwitz定理,
是
的至少
重零点,矛盾。故断言1)成立。
若
,由Hurwitz定理,可知存在一点列
,使得
。由条件可得
则
。因此证明了
。
如果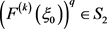 ,也就是说,存在某个
,使
。可证
,否则,
,也就是说,存在某个
,使
。可证
,否则,
,则
是一个次数至多为k的多项式。因为
的零点重级
,可得
是一个
次数为k的多项式,令
。
当
时,
这说明
。如果
,可得
,上面不等式也成立。与
矛
盾。因为
,根据Hurwitz定理,可知存在一点列
,
,使得
。根据条件可得,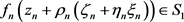 。可证,当
。可证,当
时,
。否则,
。于是,
这与
矛盾,这暗示了,若
,则
。
根据断言1)和引理2,可知
不是超越亚纯函数。
情形1.1
是一个非常数的多项式。
根据Nevanlinna第二基本定理和断言2),可知
(3)
显然,
(4)
因为F的零点重级至少为k,可知
(5)
由F的零点重级至少为
,(3),(4)和(5),可得
 (6)
(6)
(7)
由于
的零点重级均
,可知
仅有一个零点或者仅有两个不同的零点。
情形1.1.1
仅有一个零点。
令
,其中
为非零常数,对任意的
,
至少有一个零点。根据断言2),可知
至少有两个不同的零点。
情形 1.1.2
仅有两个不同的零点。
根据
的零点重级均 和(6),可知
,从而
。因此
和
,由此可知
是一个次数为4~的多项式,且
的两个不同零点的重级都为2。可证
,
。由断言2),如果
,
,这说明
不是
的重级为2的零点,矛盾。根据
和
仅有两个不同的零点,可知
的每个零点重级为2。
和(6),可知
,从而
。因此
和
,由此可知
是一个次数为4~的多项式,且
的两个不同零点的重级都为2。可证
,
。由断言2),如果
,
,这说明
不是
的重级为2的零点,矛盾。根据
和
仅有两个不同的零点,可知
的每个零点重级为2。
显然,
,令
(8)
显然,
是有理函数,它的极点来自于
零点,
。如果
是
的二~重零点,则
是
的一重零点,也是
的二重零点,这意味着
零点也是P的零点,所以P没有极点,且P是多项式。由(8),可知
,经过简单的计算,可得
,所以P仅有一个零点。对于任一
,若
,则
,这说明P至少有两个不同的零点,矛盾。
情形1.2
不是多项式的非常数有理函数。
令
(9)
其中
是复数,m是一个正整数,
和
是互素的两个多项式,且
。
假设
(10)
其中
是一个常数,t是一个正整数,
是t个正整数,
是t个不同的有限复数,
。由(9)和(10),可得到
(11)
(12)
情形1.2.1 假设
。
由Nevanlinna第二基本定理,断言1)和断言2),可知
(13)
由(9),(10)和
的零点重级均
,可得
(14)
和
(15)
结合(12)~(15),可得
。经过简单的计算,获知
. (16)
由于m,w和t都是正整数,根据(16),可知
,与
矛盾。
情形1.2.2 假设
。
从(9)~(14)可知
且
,因此
矛盾。
情形2
且
。
根据引理3,可断言g是超越亚纯函数。从(1)和(2),获知
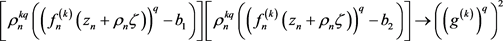 (17)
(17)
在复平面
上内闭一致收敛。可证
。如果
,可知
是一个次数至多为
,
这与
是超越亚纯函数矛盾。结合
,(1),(2),(17),
和
,可得
,即
。
根据g的级至多为2和引理4,可知,在复平面
上,g极点个数是有限的。由Nevanlinna第二基本定理,获知
(18)
从(18)可知,g是一个有理函数。矛盾。
综上所述,
在D内正规,定理1证毕。
基金项目
国家自然科学基金(编号:11271090),广东省自然科学基金(编号:2016A030310257、2015A030313346),广州大学研究生创新能力培养资助计划(2018GDJC-D28)资助。