删边梯子图和“L”型梯子图的反强迫数

doi:10.12677/AAM.2019.88159

期刊菜单

删边梯子图和“L”型梯子图的反强迫数
The Anti-Forcing Numbers of the Edge Deleted Ladder Graphs and the “L” Type Ladder Graphs

DOI: 10.12677/AAM.2019.88159, PDF, HTML, XML, 被引量国家自然科学基金支持
作者: 韩振云, 姚海元：西北师范大学数学与统计学院，甘肃兰州
关键词: 完美匹配；反强迫数；反强迫谱；删边梯子图；“L”型梯子图；Perfect Matching； Anti-Forcing Number； Anti-Forcing Spectrum； The Edge Deleted Ladder Graphs； The “L” Type Ladder Graphs

摘要: 通过分类计算的方法得到了删边梯子图的反强迫谱，进而得到了“L”型梯子图的反强迫数，过程中得到了斐波那契数列的一个组合证明。

Abstract: Through the classification calculation method, the anti-forcing number of the edge deleted ladder graphs is obtained, and the anti-forcing number of the “L” type ladder graphs is obtained. In the process, a combination proof of the Fibonacci sequence is obtained.

文章引用：韩振云, 姚海元. 删边梯子图和“L”型梯子图的反强迫数[J]. 应用数学进展, 2019, 8(8): 1352-1361. https://doi.org/10.12677/AAM.2019.88159

1. 引言

1997年，李学良研究了有强迫单边的六角系统 [1] 。2007年，Vukiěević和Trinajstić在处理有缺陷的苯类化合物的过程中推广了强迫单边的概念，提出了反强迫集和反强迫数的概念 [2] 。2016年雷洪川，叶永南和张和平引入了图的完美匹配的反强迫数的概念 [3] 。2008年Vukiěević和Trinajstić得出了卡塔型六角系统的反强迫数 [4] 。同年邓汉元给出了双链六角系统的反强迫数 [5] 。2011年张倩倩等人证明了卡塔型–亚苯基系统的反强迫数等于该系统中六角形的个数 [6] 。2013年蒋晓艳等人得到了硼氮富勒烯图的反强迫数 [7] 。2015年Hwang等引入了图的反强迫多项式的概念 [8] 。2017年邓凯和张和平证明了卡塔型六角系统的反强迫谱是连续的 [9] 。2018年姚海元等得到了循环梯状图完美匹配的反强迫谱和卢卡斯数列之间的关系 [10] 。2019年赵爽等加细了反强迫谱的概念，引入了反强迫多项式的概念，并计算了方格子等图类的反强迫多项式。总之，反强迫数的研究，大量的图类的反强迫谱/多项式有待计算 [11] 。本文主要研究了删边梯子图 $I L_{n}^{- i}$ 的反强迫数，得到了 $I L_{n}^{- i}$ 的反强迫谱。并通过收缩 $I L_{n}^{- i}$ 两条水平边的方法得到了“L”型梯子图的反强迫数，由此得到了几个与斐波那契数列和卢卡斯数列相关的结果。本文中将 $a \equiv b (\mod 2)$ 简记为 $a \equiv b$ ，表示 $a, b$ 同奇偶。

2. 预备知识

设M是G的一个完美匹配， $S \subseteq E (G)$ ，若M是 $G - S$ 的唯一完美匹配，则称S为M的一个反强迫集。M的最小反强迫集的大小称为M的反强迫数，记为 $a f (G, M)$ 。图G的最小反强迫数是一个整体概念，其值等于G中所有完美匹配反强迫数的最小值，记为 $a f (G)$ 。类似的，图G的反强迫数的最大值叫做G的最大反强迫数，记为 $A f (G)$ 。设 $A$ 是G中M-交错圈组成的集合。若 $A$ 中任意两个M-交错圈不交或仅交于M中的边，我们称 $A$ 是一个相容M-交错集。图G的最大相容M-交错集的大小记为 $c^{'} (M)$ 。

引理1 [11] 若M是图G的一个完美匹配，则 $a f (G, M) \geq c^{'} (M)$ ，若图G是平面二部图，则 $a f (G, M) = c^{'} (M)$ 。

定义1 我们把一个梯子图 $L_{n} = P_{n} \times P_{2}$ 水平放置，其顶点从上到下、从左到右依次记为 $a_{1}, a_{2}, \dots, a_{n}, b_{1}, b_{2}, \dots, b_{n}$ ，而后我们把在 $L_{n}$ 中删去第i条竖直边 $a_{i} b_{i}$ 得到的图(如图1所示)称为删去第i条竖直边的删边梯子图。记为 $I L_{n}^{- i}$ 。

Figure 1. The edge deleted ladder graphs $I L_{n}^{- i}$

图1. 删边梯子图 $I L_{n}^{- i}$

定义2 设 $I L_{n}^{- i}$ 是一个删边梯子图，我们将 $I L_{n}^{- i}$ 的两边 $a_{i - 1} a_{i}, a_{i} a_{i + 1}$ 收缩得到的图称为“L”型梯子图(如图2所示)，记为 $L L_{n}^{- i}$ 。

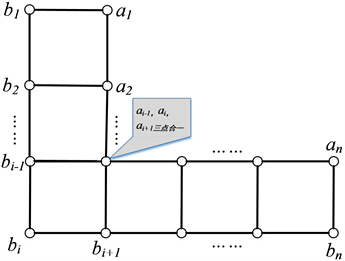
Figure 2. “L” type ladder graphs $L L_{n}^{- i}$

图2. “L”型梯子图 $L L_{n}^{- i}$

在 $I L_{n}^{- i}$ 和 $L L_{n}^{- i}$ 中将形如 $a_{i} a_{i + 1}, b_{i} b_{i + 1}$ 的边称为水平边，而形如 $a_{i} b_{i}$ 的边称为垂直边。当给定该图的一个完美匹配M，若 $a_{i} a_{i + 1}, b_{i} b_{i + 1} \in M$ ，则将其称为水平匹配边；若 $a_{i} b_{i} \in M$ ，则将其称为垂直匹配边，垂直匹配边的总数记为p，特别的形如 $a_{j} b_{j} \in M (2 \leq j \leq n - 1)$ 称为内部垂直匹配边。

类似文献 [10] 引理3，我们可证

引理2 若M是 $L_{n}$ 的包含 $p (0 \leq p \leq n)$ 条垂直匹配边的完美匹配，则

$a f (L_{n}, M) = {\begin{array}{l} \frac{n}{2}, & p = 0 \\ \frac{n + p - 2}{2}, & p \geq 1 \end{array}$ 。

引理3 若M是 $I L_{n}$ 的包含 $p (0 \leq p \leq n - 2)$ 条垂直匹配边的完美匹配，则 $p \equiv n$ 且其水平匹配边必成对出现，即 $a_{m} a_{m + 1} \in M \Leftrightarrow b_{m} b_{m + 1} \in M$ 。

证明设M是 $I L_{n}$ 的完美匹配，若 $I L_{n}$ 的某一对水平边 $a_{m} a_{m + 1} \in M, b_{m} b_{m + 1} \notin M$ ，则整个图无垂直匹配边且至少存在两个M-非饱和的点，与M是 $I L_{n}$ 的完美匹配矛盾，所以 $a_{m} a_{m + 1} \in M$ 时必有 $b_{m} b_{m + 1} \in M$ 。不妨设M有2q条水平匹配边，则 $p + 2 q = | M | = n$ ，因此 $p \equiv n (\mod 2)$ 。

引理4 设M是删边梯子图 $I L_{n}^{- i}$ 的一个完美匹配， $a_{h} b_{h}$ 是M的内部垂直匹配边，不妨设 $h < i$ ， $M_{1} = M \cap E (L_{h})$ ； $M_{2} = M \cap E (I L_{n - h + 1}^{- (i - h + 1)})$ 。则

$a f (I L_{n}^{- i}, M) = a f (L_{h}, M_{1}) + a f (I L_{n - h + 1}^{- (i - h + 1)}, M_{2})$ 。

证明因为 $a_{h} b_{h} \in M$ ，所以 $L_{h} \cap I L_{n - h + 1}^{- (i - h + 1)} = {a_{h} b_{h}}$ ， $M_{1}, M_{2}$ 分别是 $L_{h}, I L_{n - h + 1}^{- (i - h + 1)}$ 上的完美匹配，且 $M_{h} \cap M_{n - h + 1} = {a_{h} b_{h}}$ ， $M_{h} \cup M_{n - h + 1} = M$ 。

一方面，令 $A$ 是 $I L_{n}^{- i}$ 的相容M-交错集，令 $A_{1} = A \cap E (L_{h})$ ， $A_{2} = A \cap E (I L_{n - h + 1}^{- (i - h + 1)})$ 。由于 $a_{h} b_{h} \in M$ ，

$a_{h - 1} a_{h}, a_{h} a_{h + 1}, b_{h - 1} b_{h}, b_{h} b_{h + 1} \notin M$ 。对于任意的M-交错圈 $C \in A$ ， $a_{h - 1} a_{h}$ 和 $a_{h} a_{h + 1}$ 不能同时在C中， $b_{h - 1} b_{h}$ 和 $b_{h} b_{h + 1}$ 也不能同时在C中。若 $a_{h - 1} a_{h} \in C$ ，则 $a_{h} b_{h}, b_{h - 1} b_{h} \in C$ ，此时 $C \in A_{1}$ 是一个 $M_{1}$ -交错圈。同理，若 $a_{h} a_{h + 1} \in C$ ，则 $a_{h} b_{h}, b_{h} b_{h + 1} \in C$ ，因此 $C \in A_{2}$ 是一个 $M_{2}$ -交错圈。否则就有 $a_{h} b_{h} \notin C$ 。所以 $C \in A$ 是一个 $M_{1}$ -交错圈或 $M_{2}$ -交错圈，因此 $A \subseteq A_{1} \cup A_{2}$ ，即 $A = A_{1} \cup A_{2}$ 。对任意的 $C_{1}, C_{2} \in A$ ，若 $C_{1}, C_{2} \in A_{1}$ (或 $A_{2}$ )，则 $C_{1}, C_{2}$ 是 $M_{1}$ -相容(或 $M_{2}$ -相容)的。不然是 $M_{j}$ -相容的， $j = 1, 2$ ，故 $c^{'} (M) \leq c^{'} (M_{1}) + c^{'} (M_{2})$ 。

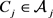另一方面，令 $A_{j}$ 是相容 $M_{j}$ -交错集， $j = 1, 2$ ，令 $A = A_{1} \cup A_{2}$ 。设 $C_{1}, C_{2} \in A$ 是两个任意M-交错圈，

若 $C_{1}, C_{2} \in A_{j}$ ，则 $C_{1}, C_{2}$ 是相容 $M_{j}$ -交错集， $j = 1, 2$ ，否则设 $C_{1} \in A_{1}$ ， $C_{2} \in A_{2}$ 。若 $C_{1} \cap C_{2} = {a_{h} b_{h}}$ ，

则 $C_{1}$ 和 $C_{2}$ 是M-相容的。若 $C_{1}, C_{2}$ 中最多有一个圈包含 $a_{h} b_{h}$ ，则 $C_{1}$ 和 $C_{2}$ 不交， $C_{1}$ 和 $C_{2}$ 也是M-相容的。因此，

$c^{'} (M) \geq c^{'} (M_{1}) + c^{'} (M_{2})$ 。

综上所述， $c^{'} (M) = c^{'} (M_{1}) + c^{'} (M_{2})$ ，故

$a f (I L_{n}^{- i}, M) = a f (L_{h}, M_{1}) + a f (I L_{n - h + 1}^{- (i - h + 1)}, M_{2})$ 。

引理5 [11] 图G的反强迫多项式是一个有如下形式的计数多项式：

$A f (G, x) = \sum_{M \in M (G)} x^{a f (G, M)}$ 。

若G没有完美匹配，则 $A f (G, x) = 0$ ；若G有唯一的完美匹配，则 $A f (G, x) = 1$ 。特别地，对空图我们有 $A f (G, x) = 1$ 。

合并反强迫多项式的同类项，得到如下结论。

引理6 [11] 图G的反强迫多项式有如下等价定义：

$A f (G, x) = \sum_{i = a f (G)}^{A f (G)} v (G, i) x^{i}$ ，

其中 $v (G, i)$ 表示反强迫数为i的完美匹配的个数。

引理7 [8] 图G的反强迫多项式有如下性质：

1) $A f (G, 1)$ 表示G的完美匹配的个数；

2) ${\frac{d}{d x} A f (G, x) |}_{x = 1}$ 表示G的所有完美匹配的反强迫数之和；

3) $\frac{{\frac{d}{d x} A f (G, x) |}_{x = 1}}{A f (G, 1)}$ 表示G的平均反强迫数。

引理8 [10] 梯子图 $L_{n}$ 中含有 $2 q = n - p$ 条水平匹配边的完美匹配个数是 $(\begin{matrix} n - q \\ q \end{matrix}) = (\begin{matrix} \frac{n + p}{2} \\ p \end{matrix})$ 。

3. $I L_{n}^{- i}$ 的反强迫数和反强迫谱

定理1 若M是删边梯子图 $I L_{n}^{- i}$ 的含有 $p \leq 2$ 条非内部垂直匹配边的完美匹配，则

$a f (I L_{n}^{- i}, M) = {\begin{array}{l} \frac{n - 2}{2}, & p = 0 \\ \frac{n - 1}{2}, & p = 1 且 i 为偶数 \\ \frac{n - 3}{2}, & p = 1 且 i 为奇数 \\ \frac{n - 2}{2}, & p = 2 \end{array}$ 。

证明因为 $I L_{n}^{- i}$ 是一个不可分解删边梯子图，所以由引理1和分解引理知 $I L_{n}^{- i}$ 的完美匹配M有 $p (p = 0, 1, 2)$ 条垂直匹配边。下面根据p值分情况讨论：

情形1 若 $p = 0$ ，此时删边梯子图 $I L_{n}^{- i}$ 无垂直匹配边且n为偶数，匹配方式如图3所示。

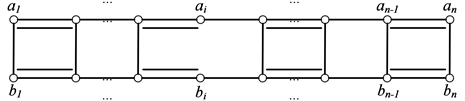
Figure 3. The case $p = 0$ in $I L_{n}^{- i}$

图3. $I L_{n}^{- i}$ 中 $p = 0$ 的情形

所以 $a f (I L_{n}^{- i}, M) = q - 1 = \frac{n - 2}{2}$ ；

情形2 若 $p = 1$ ，此时删边梯子图 $I L_{n}^{- i}$ 仅有一条垂直匹配边，不妨设 $a_{1} b_{1}$ 是这条垂直匹配边，当i为偶数时，匹配方式如图4(a)所示；i为奇数时，匹配方式如图4(b)所示。

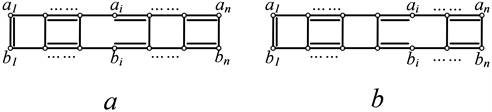
Figure 4. The case $p = 1$ (a) i is even; (b) i is odd

图4. $p = 1$ 情形(a) i为偶数；(b) i为奇数

令 $A$ 是 $I L_{n}^{- i}$ 的相容M-交错集，因为一个M-交错圈至少包含两条垂直边，当i是偶数时，所有交错4圈和交错圈 $a_{1} a_{2} \dots a_{i} a_{i + 1} b_{i + 1} b_{i} \dots b_{2} b_{1} a_{1}$ 是M-相容的，且用完了每一个垂直单边，又因包含 $a_{1} b_{1}$ 的M-相容交

错圈必包含 $a_{1} a_{2}$ ，故 ${| A |}_{\max} = \frac{n - 1}{2}$ ；当i是奇数时，因没有M-交错圈能包含 $a_{1} b_{1}$ 和 $a_{i - 1} b_{i - 1}$ ，而其余垂直边均包含在M-相容交错4圈中，故 ${| A |}_{\max} = \frac{n - 3}{2}$ 。因此由引理1知

$a f (I L_{n}^{- i}, M) = {\begin{array}{l} q = \frac{n - 1}{2}, & i 为偶数 \\ q - 1 = \frac{n - 3}{2}, & i 为奇数 \end{array}$ ；

情形3 $p = 2$ ，此时删边梯子图 $I L_{n}^{- i}$ 有两条垂直匹配边且分别位于两边，匹配方式如图5所示。

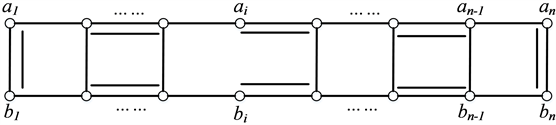
Figure 5. $p = 2$ in $I L_{n}^{- i}$

图5. $I L_{n}^{- i}$ 中 $p = 2$

所以由引理1知

$a f (I L_{n}^{- i}, M) = q = \frac{n - 2}{2}$

综上，定理得证。

在 $I L_{n}^{- i}$ 中，我们把位于 $a_{i} b_{i}$ 左边的垂直匹配边的总数记为 $p_{1}$ ，位于 $a_{i} b_{i}$ 右边的垂直匹配边的总数记为 $p_{2}$ ，显然有 $p = p_{1} + p_{2} \equiv n$ 。

定理2 若M是删边梯子图 $I L_{n}^{- i}$ 的一个包含p条垂直匹配边的完美匹配，则

$a f (I L_{n}^{- i}, M) = {\begin{matrix} \frac{n + p - 2}{2}, & p_{1} = 0, 且 a_{i - 1} a_{i} \in M 或 p_{2} = 0 且 a_{i} a_{i + 1} \in M, \\ \frac{n + p - 4}{2}, & 其它 . \end{matrix}$

证明当 $I L_{n}^{- i}$ 无垂直匹配边则 $p_{1} = p_{2} = 0$ ；当 $a_{i} b_{i}$ 只有一侧存在垂直匹配边则 $p_{1} = 0, p_{2} \neq 0$ 或 $p_{1} \neq 0, p_{2} = 0$ ；当 $a_{i} b_{i}$ 两侧都存在垂直匹配边则 $p_{1} p_{2} \geq 1$ 。下面分情况讨论：

情况1若 $p_{1} = p_{2} = 0$ ，整个删边梯子图无垂直匹配边，即 $p = 0$ ，所以由定理1易知

$a f (I L_{n}^{- i}, M) = q - 1 = \frac{n - 2}{2} = \frac{n + p - 2}{2}$ ；

情况2 ① 若 $p_{1} = 0, p_{2} \neq 0$ ， $a_{i} b_{i}$ 只有右侧存在垂直匹配边，不妨设离 $a_{i} b_{i}$ 最近的右侧垂直匹配边为 $a_{j} b_{j}$ ，由引理4可知整个删边梯子图可以从 $a_{j} b_{j}$ 处分解成两个片段，第一片段为删边梯子图 $I L_{j}^{- i}$ ，第二

片段为梯子图 $L_{n - j + 1}$ ，此处 $p_{2} = p$ 。定义 $M_{1} = M \cap E (I L_{j}^{- i})$ 是 $I L_{j}^{- i}$ 上的完美匹配； $M_{2} = M \cap E (L_{n - j + 1})$ 是 $L_{n - j + 1}$ 上的完美匹配，由引理2和引理4易知

$a f (I L_{j}^{- i}, M_{1}) = {\begin{array}{l} \frac{j - 1}{2} ， & i 为偶数 \\ \frac{j - 3}{2} ， & i 为奇数 \end{array}$ ；

$a f (L_{n - j + 1}, M_{2}) = \frac{n - j + 1 + p_{2} - 2}{2}$ 。

故

当i为偶数时，即 $a_{i - 1} a_{i}$ 为匹配边时

$\begin{matrix} a f (I L_{n}^{- i}, M) = a f (I L_{j}^{- i}, M_{1}) + a f (L_{n - j + 1}, M_{2}) \\ = \frac{j - 1}{2} + \frac{n - j + 1 + p_{2} - 2}{2} \\ = \frac{n + p - 2}{2} \end{matrix}$

当i为奇数时，即 $a_{i} a_{i + 1}$ 为匹配边时

$\begin{matrix} a f (I L_{n}^{- i}, M) = a f (I L_{j}^{- i}, M_{1}) + a f (L_{n - j + 1}, M_{2}) \\ = \frac{j - 3}{2} + \frac{n - j + 1 + p_{2} - 2}{2} \\ = \frac{n + p - 4}{2} \end{matrix}$ 。

② $p_{1} \neq 0, p_{2} = 0$ 时同理可得

$a f (I L_{n}^{- i}, M) = {\begin{array}{l} \frac{n + p - 2}{2}, & a_{i} a_{i + 1} 为匹配边 \\ \frac{n + p - 4}{2}, & a_{i - 1} a_{i} 为匹配边 \end{array}$

情况3 若 $p_{1}, p_{2} \geq 1$ ， $a_{i} b_{i}$ 两侧都存在垂直匹配边不妨记离 $a_{i} b_{i}$ 最近的左右侧竖直匹配边分别为 $a_{j} b_{j}, a_{k} b_{k}$ ，则梯子图 $I L_{n}^{- i}$ 可分解成三段，三个片段分别为 $L_{j}$ ， $I L_{k - j + 1}^{- (i - j + 1)}$ ， $L_{n - k + 1}$ ；不妨记 $M_{1} = M \cap E (L_{j})$ ， $M_{2} = M \cap E (I L_{k - j + 1}^{- (i - j + 1)})$ ， $M_{3} = M \cap E (L_{n - k + 1})$ 分别是三个片段上的完美匹配， $p_{1}$ 和 $p_{2}$ 分别是 $L_{j}$ 和 $L_{n - k + 1}$ 上竖直匹配边的数目，显然 $p_{1} + p_{2} = p$ 。由引理2，定理1和引理4可得

$a f (L_{j}, M_{1}) = \frac{j + p_{1} - 2}{2}$ ；

$a f (I L_{k - j + 1}^{- (i - j + 1)}, M_{2}) = \frac{k - j + 1 - 2}{2}$ ；

$a f (L_{n - k + 1}, M_{3}) = \frac{n - k + 1 + p_{2} - 2}{2}$ 。

所以

$\begin{matrix} a f (I L_{n}^{- i}, M) = a f (L_{j}, M_{1}) + a f (I L_{k - j + 1}^{- (i - j + 1)}, M_{2}) + a f (L_{n - k + 1}, M_{3}) \\ = \frac{j + p_{1} - 2}{2} + \frac{k - j + 1 - 2}{2} + \frac{n - k + 1 + p_{2} - 2}{2} \\ = \frac{n + p - 4}{2} \end{matrix}$

综上三种情况，定理得证。

定理3 $I L_{n}^{- i}$ 的反强迫谱为

$S p e c_{a f} (I L_{n}^{- i}) = {\begin{array}{l} {\frac{n - 3}{2} + f, \frac{n - 1}{2} + f, \dots, \frac{n + p - 4}{2} + f, \dots, \frac{2 n - 5}{2} + f}, & n \geq 3 且 n 为奇数 \\ {\frac{n - 2}{2}, \frac{n - 2}{2} + f, \dots, \frac{n + p - 4}{2} + f, \dots, \frac{2 n - 5}{2} + f}, & n \geq 4 且 n 为偶数 \end{array}$

其中将 $I L_{n}^{- i}$ 按所有内部垂直匹配边分解为片段时，若包含 $a_{i}$ 的片段中仅含唯一的垂直匹配边 $a_{j} b_{j}$ ，且 $i \equiv j$ 时 $f = 1$ ，否则 $f = 0$ 。

证明按照 $I L_{n}^{- i}$ 的完美匹配M中的垂直匹配边的条数p和 $i, j$ 的同奇偶性分情况讨论：

情形1 若 $p = 0$ ，此时

$a f (I L_{n}^{- i}, M) = \frac{n - 2}{2}$ ；

情形2 若 $p = 1$ ，此时包含 $a_{i}$ 的片段中仅含唯一的垂直匹配边 $a_{j} b_{j}$ ，根据定理1情况2可知

当 $i \equiv j$ 时，

$a f (I L_{n}^{- i}, M) = \frac{n + p - 2}{2} = \frac{n - 1}{2}$ ；

当 $i \equiv j$ 时，

$a f (I L_{n}^{- i}, M) = \frac{n + p - 4}{2} = \frac{n - 3}{2}$ 。

此时

$a f (I L_{n}^{- i}, M) = \frac{n + p - 4}{2} + f = \frac{n - 3}{2} + f$

情形3 若 $p \geq 2$ ，这时包含 $a_{i}$ 的片段可能包含一条或两条垂直匹配边。

情形3.1 当包含 $a_{i}$ 的片段中仅含唯一的垂直匹配边 $a_{j} b_{j}$ 。若 $i \equiv j$ ，

$a f (I L_{n}^{- i}, M) = \frac{n + p - 2}{2} = \frac{n + p - 4}{2} + 1 = \frac{n + p - 4}{2} + f$ ；

否则 $a f (I L_{n}^{- i}, M) = \frac{n + p - 4}{2} = \frac{n + p - 4}{2} + 0 = \frac{n + p - 4}{2} + f$ ；

情形3.2 当包含 $a_{i}$ 的片段包含两条垂直匹配边时，

$a f (I L_{n}^{- i}, M) = \frac{n + p - 4}{2} = \frac{n + p - 4}{2} + f$ 。

综上，结论成立。

根据以上结论，我们可以得出 $I L_{n}^{- i}$ 的反强迫多项式，特别当 $n \equiv i \equiv 1$ 时有

推论1 设 $n, i$ 都为奇数，则有

$A f (I L_{n}^{- i}, x) = \sum_{p = 1}^{n - 2} | M_{p} | x^{\frac{n + p - 4}{2}}$ 。

其它情况下其形式过于复杂，在此不作赘述，仅给出几个具体例子：

$A f (I L_{8}^{- 3}, x) = 7 x^{3} + 9 x^{4} + 2 x^{5}$ ，

$A f (I L_{7}^{- 4}, x) = 8 x^{3} + 4 x^{4}$ ，

$A f (I L_{16}^{- 6}, x) = 19 x^{7} + 141 x^{8} + 303 x^{9} + 275 x^{10} + 120 x^{11} + 25 x^{12} + 2 x^{13}$ 。

推论2

$a f (I L_{n}^{- i}) = {\begin{array}{l} \frac{n - 3}{2} + f, & n \geq 3 且 n 为奇数 \\ \frac{n - 2}{2}, & n \geq 4 且 n 为偶数 \end{array}$ 。

推论3 $A f (I L_{n}^{- i}) = n - 3 + f$ 。

定理4 若 $I L_{n}^{- i}$ 含p条垂直匹配边，则其完美匹配个数为

$| M_{p} | = \sum_{p_{1} = 0}^{p} (\begin{matrix} ⌊ \frac{i - 1 + p_{1}}{2} ⌋ \\ p_{1} \end{matrix}) (\begin{matrix} ⌊ \frac{n - i + p - p_{1}}{2} ⌋ \\ p - p_{1} \end{matrix})$ 。

证明设 $a_{i}$ 左边和右边分别有 $p_{1}, p_{2}$ 条垂直匹配边， $p_{1} + p_{2} = p$ 。

情形1 当i为偶数时，

① $a_{i - 1} a_{i} \in M$ ， $p_{1}$ 必为偶数，则 $I L_{n}^{- i}$ 可以从 $a_{i - 2} a_{i - 1}$ 和 $a_{i} a_{i + 1}$ 处分解开，由引理8知

${| M |}_{p} = \sum_{\begin{array}{l} p_{1} = 0 \\ p_{1} \equiv i \end{array}}^{p} (\begin{matrix} \frac{i - 2 + p_{1}}{2} \\ p_{1} \end{matrix}) (\begin{matrix} \frac{n - i + p_{2}}{2} \\ p_{2} \end{matrix})$ ；

② $a_{i - 1} a_{i} \notin M$ ， $p_{1}$ 必为奇数，同理

${| M |}_{p} = \sum_{\begin{array}{l} p_{1} = 1 \\ p_{1} \equiv i \end{array}}^{p} (\begin{matrix} \frac{i - 2 + p_{1}}{2} \\ p_{1} \end{matrix}) (\begin{matrix} \frac{n - i + p_{2}}{2} \\ p_{2} \end{matrix})$ ；

情形2 当i为奇数时，

① $a_{i - 1} a_{i} \in M$ ， $p_{1}$ 必为奇数，

${| M |}_{p} = \sum_{\begin{array}{l} p_{1} = 1 \\ p_{1} \equiv i \end{array}}^{p} (\begin{matrix} \frac{i - 1 + p_{1}}{2} \\ p_{1} \end{matrix}) (\begin{matrix} \frac{n - i - 1 + p_{2}}{2} \\ p_{2} \end{matrix})$

② $a_{i - 1} a_{i} \notin M$ ， $p_{1}$ 必为偶数，

${| M |}_{p} = \sum_{\begin{array}{l} p_{1} = 0 \\ p_{1} \equiv i \end{array}}^{p} (\begin{matrix} \frac{i - 1 + p_{1}}{2} \\ p_{1} \end{matrix}) (\begin{matrix} \frac{n - i - 1 + p_{2}}{2} \\ p_{2} \end{matrix})$

综上得，

$\begin{matrix} | M_{p} | = \sum_{\begin{array}{l} p_{1} = 0 \\ p_{1} \equiv i \end{array}}^{p} (\begin{matrix} \frac{i - 2 + p_{1}}{2} \\ p_{1} \end{matrix}) (\begin{matrix} \frac{n - i + p - p_{1}}{2} \\ p - p_{1} \end{matrix}) + \sum_{\begin{array}{l} p_{1} = 0 \\ p_{1} \equiv i \end{array}}^{p} (\begin{matrix} \frac{i - 1 + p_{1}}{2} \\ p_{1} \end{matrix}) (\begin{matrix} \frac{n - i - 1 + p - p_{1}}{2} \\ p - p_{1} \end{matrix}) \\ = \sum_{p_{1} = 0}^{p} (\begin{matrix} ⌊ \frac{i - 1 + p_{1}}{2} ⌋ \\ p_{1} \end{matrix}) (\begin{matrix} ⌊ \frac{n - i + p - p_{1}}{2} ⌋ \\ p - p_{1} \end{matrix}) \end{matrix}$

定理得证。

我们用在梯子图的所有完美匹配中减去含 $a_{i} b_{i}$ 的完美匹配的方法就可以得到以下推论。

推论4 $I L_{n}^{- i}$ 含p条竖直匹配边完美匹配个数

$| M_{p} | = (\begin{matrix} \frac{n + p}{2} \\ p \end{matrix}) - \sum_{p_{1} = 0}^{z} (\begin{matrix} \frac{i - 1 + p_{1}}{2} \\ p_{1} \end{matrix}) (\begin{matrix} \frac{n - i + p_{2}}{2} \\ p_{2} \end{matrix})$ ，

其中 $z = \min {p - 1, i - 1}, p_{1} + p_{2} = p - 1, n \equiv p, p_{1} \equiv i - 1$ 。

推论5 删边梯子图 $I L_{n}^{- i}$ 完美匹配数

$| M | = F_{n + 1} - F_{i} F_{n - i + 1} = \sum_{p = 0}^{n - 2} | M_{p} |$ 。

由此可知，对于给定的i， $I L_{n}^{- i}$ 的完美匹配数是一个具有特定初值的斐波那契数列。特别地，当 $i = 2, 3$ 时分别为斐波那契数列和卢卡斯数列。

4. “L”型梯子图 $L L_{n}^{- i}$ 的反强迫数

设 $L L_{n}^{- i}$ 是收缩 $I L_{n}^{- i}$ 的 $a_{i - 1} a_{i}$ 和 $a_{i} a_{i + 1}$ 两条边得到的“L”型梯子图。任取 $I L_{n}^{- i}$ 的完美匹配 $M^{i}$ ，必有 $a_{i - 1} a_{i}, a_{i} a_{i + 1}$ 之一(记为e)属于 $M^{i}$ ，则 $M = M^{i} - e$ 是 $L L_{n}^{- i}$ 的完美匹配，反之亦然。因而 $I L_{n}^{- i}$ 中的 $M^{i}$ -交错圈和 $L L_{n}^{- i}$ 中的M-交错圈一一对应。进一步我们有

定理5 $a f (L L_{n}^{- i}, M) = a f (I L_{n}^{- i}, M^{i})$ 。

证明不妨设 $e = a_{i - 1} a_{i} \in M^{i}$ ( $M = M^{i} - e$ )，任取 $M^{i}$ 的最小反强迫集 $S_{a}$ 。若 $a_{i} a_{i + 1} \notin S_{a}$ ，则令 ${S^{'}}_{a} = S_{a}$ ，否则令 ${S^{'}}_{a} = S_{a} - a_{i} a_{i + 1} + b_{i} b_{i + 1}$ ，由引理3可知 ${S^{'}}_{a}$ 就是M的一个反强迫集。因此

$a f (I L_{n}^{- i}, M^{i}) \geq a f (L L_{n}^{- i}, M)$ 。

反之，不妨设 $b_{i - 1} b_{i} \in M$ ，记 $e = a_{i - 1} a_{i}$ ，则必有 $M^{i} = M + e$ 是 $L L_{n}^{- i}$ 的一个完美匹配且 $e \in M^{i}$ ，因此 ${S^{'}}_{a}$ 也是 $M^{i}$ 的一个反强迫集。因此

$a f (I L_{n}^{- i}, M^{i}) \leq a f (L L_{n}^{- i}, M)$ 。

综上，结论成立。

类似地，我们可证明

推论6 $f (L L_{n}^{- i}, M) = f (I L_{n}^{- i}, M^{i})$ 。

推论7 设 $L L_{n}^{- i}$ 是一个“L”型梯子图，M是 $L L_{n}^{- i}$ 的一个有p条垂直匹配边的完美匹配， $a_{i} b_{i}$ 左、右侧的垂直匹配边数分别记为 $p_{1}, p_{2}$ ，我们有

$a f (L L_{n}^{- i}, M) = {\begin{matrix} \frac{n + p - 2}{2} ， & p_{1} = 0 且 b_{i - 1} b_{i} \in M 或 p_{2} = 0 且 b_{i} b_{i + 1} \in M, \\ \frac{n + p - 4}{2} ， & 其它 . \end{matrix}$

基金项目

国家自然科学基金(11401475)。

NOTES

^*通讯作者。

参考文献

[1]	Li, X. (1997) Hexagonal Systems with Forcing Single Edges. Discrete Applied Mathematics, 72, 295-301. https://doi.org/10.1016/0166-218X(95)00116-9
[2]	Vukiěević, D. and Trinajstić, N. (2007) On the Anti-Forcing Number of Benzenoids. Journal of Mathematical Chemistry, 42, 575-583. https://doi.org/10.1007/s10910-006-9133-6
[3]	Lei, H., Yeh, Y. and Zhang, H. (2016) Anti-Forcing Numbers of Perfect Matchings of Graphs. Discrete Applied Mathematics, 202, 95-105. https://doi.org/10.1016/j.dam.2015.08.024
[4]	Vukiěević, D. and Trinajstić, N. (2008) On the Anti-Kekule Number and Anti-Forcing Number of Cata-Condensed Benzenoids. Mathematics in Chemistry, 43, 719-726. https://doi.org/10.1007/s10910-006-9223-5
[5]	Deng, H. (2008) The Anti-Forcing Number of Double Hexagonal Chains. MATCH—Communications in Mathematical and in Computer Chemistry, 60, 183-192.
[6]	Zhang, Q., Bian, H. and Vumar, E. (2011) On the Anti-Kekule Number and Anti-Forcing Number of Cata Condensed Phenylenes. MATCH—Communications in Mathematical and in Computer Chemistry, 65, 799-806.
[7]	蒋晓艳, 程晓胜. 硼氮富勒烯图的反强迫数[J]. 湖南师范学院学报: 自然科学版, 2013, 33(3): 28-30.
[8]	Hwang, H.-K., Lei, H., Yeh, Y.-N. and Zhang, H. (2015) Distribution of Forcing and Anti-Forcing Numbers of Random Perfect Matchings on Hexagonal Chains and Crowns. http://140.109.74.92/hk/?p=873
[9]	Deng, K. and Zhang, H. (2017) Anti-Forcing Spectrum of Any Cata-Condensed Hexagonal System Is Continuous. Frontiers of Mathematics in China, 12, 325-337. https://doi.org/10.1007/s11464-016-0605-0
[10]	姚海元, 王杰彬, 王旭. 循环梯状图的完美匹配的反强迫谱与卢卡斯数[J]. 西北师范大学学报: 自然科学版, 2018, 54(2): 21-25.
[11]	Zhao, S. and Zhang, H. (2019) Forcing and Anti-Forcing Polynomials of Perfect Matchings for Some Rectangle Grids. Journal of Mathematical Chemistry, 57, 202-225. https://doi.org/10.1007/s10910-018-0944-z

为你推荐

友情链接