地球自转速度随其年龄增长呈反比例单支双曲线衰减

Attenuation of the Earth’s Rotation Speeds with Its Age Accretion as a Branch of Hyperbola of an Inverse Proportion

摘要: 基于地球现今年龄、历时年龄与地球自转速度三者之间的关系提出地球自转速度表达式为：ω_x=Aω_q/(A-T_x) 。该式显示地球自转速度(ω_x)与地球历时年龄(A−T_x)呈反比例变化，即：随年龄增长地球自转速度减慢，相应地，地球的日长增加。该式所对应的图像为反比例函数在第一象限的单支双曲线，它可划分为三大区段(其第II区段可分为两个亚区段)，分别对应了地球自转速度衰减的三个阶段，并可进一步区分出12个可能的地球自转速度半衰期。在距今4282Ma时，赤道自转速度已经衰减到第一宇宙速度之下，此为水成变质岩的年龄值上限。元古代半衰期和显生代半衰期的计算结果可得到化石生长线证据的验证，其余结果有待发现古老日长的可靠数据来校验。地球的历时年龄与该年龄时的自转速度之积为常数，称地球自转行程常数。本文还计算了未来两个时间点的日长，预测209.6 Ma后地球日长可达25小时。

Abstract: Based on the relationships among the Earth’s present age, the lasted ages and the rotation speeds, a calculating formula for the Earth’s rotation speeds, ω_x = Aω_q/(A − T_x), is put forward in this paper. The expression comprehends that an inverse proportion existing between the Earth’s rotation speeds (ω_x) and the Earth's lasted ages (A − T_x), namely, with accretion of the Earth’s age, the rotation speed decreases gradually, and correspondingly, the Earth’s day-long becomes longer. The relevant graph of the expression is a branch of hyperbola in the first quadrant with an inverse proportion function. The branch of hyperbola which describes the attenuation of the earth's rotation speeds can be divided into three major sections, and the second section divided further into two sub-sections. They should be homological with the three main stages of the attenuation of the Earth’s rotation speeds respectively, and 12 possible half-lives of attenuation can be distinguished. By 4282 Ma, the rotation linear speed of the Earth’s equator might attenuate to less than the first universal velocity, and the last window for air and water vapor escaping from the Earth might be closed, so that the hydro-metamorphic rocks with an age more than 4300 Ma, might not be found. The calculated results for the half-lifes of the Proterozoic Era and the Phanerozoic Era can be verified by the fossil’s growth lines preserved in the strata, and the rest part of the branch curve needs to be verified by finding more reliable data on older day-longs. The products of the Earth’s lasted ages and the rotation speeds at that time point should be a constant, which is named the throw constant of the Earth’s rotation. Also, the paper calculates two examples for the day-longs in the future, and forecasts that after 209.6 Ma, the Earth will have 25 hours per day.

1. 引言

笔者曾提出：地球自转的速度随年龄增长是逐渐变慢的(故1年的天数变少)，相应地，地球的日长(day-long，即1天有多少小时)则是逐渐增加的；由于化石的生长线记录了它那个时间点的地球1年有多少天，构建起地球年龄、地层时代和自转速度(日长)这三者的函数关系后，即可用化石生长线记录的日长推定化石赋存地层的年龄 [1] [2] 。本文将进一步探讨地球自转速度随其年龄增长的变化规律，构建计算地球自转速度的数学表达式和它与地球年龄之间的函数关系，并用它来预测若干年后的地球日长。

尽管地球自转的扰动因素众多而复杂，目前有关的各种理论还属于假说，但普遍倾向地球自转速度逐渐变慢。减速模型之一是潮汐摩擦模式；由于激光测距技术的采用，提高了计算结果的精度。中国科学院测地研究所2016年9月1日发布的地球日长百年变化率为2.24 ± 0.08毫秒/世纪。另一种模式是天文学家利用古代日食、月食记录构建的计算模型。20世纪50年代开始探索利用最近100年的日食、月食记录；90年代，Stephenson等利用2690年中累积的天文资料，得到日长的增长为1.7毫秒/世纪。2017年他们利用2735年里累积的日食、月食记录，得到新的更精确的结果为1.8毫秒/世纪(详见本文)。此外，20世纪60年代，尹赞勋、乐森璕和Wells等利用珊瑚或腕足类化石上保存的生长线，证实了自古生代以来地球自转速度的减速状态，启发我们把生长线发展为测定化石保存地层时代年龄的一种新方法。

是否可以利用上述地质资料来研究漫长地质长历史时期中的日长变化情况？本文提出的一个新思路，是利用两个永远对地球自转速度起消减作用的因素构成地球的惯性矩。因素之一是每天有大量宇宙物质落入地球，不断微量累积，增加地球的质量。因素之二是每天一次的固体潮使地球半径发生伸缩弹性变形，当半径拉长时即造成一次自转制动作用。该效应也可以微量累积。这两个因素正好构成地球惯性矩的全部变量：地球质量与半径。假设地球惯性矩在地质历史中成微量线性变化，则得到表达地球年龄的近似公式和地球自转速度的表达公式。虽然利用该新思路探讨地史时期的地球自转速度的衰减给出的曲线是粗糙的，近似的，毕竟指出了速度衰减的一个大趋势，其结果得到晚元古以来化石记录的日长证据的支持，预测的未来日长变化也可与天文学的研究结果大致对应。

2. 地球自转速度表达式

文献 [1] 中提出：现今地球年龄、地史期间的某时间点和该时间点地球自转角速度这三个參变量之间的关系，是一个表达地球年龄的近似公式：

$A={\omega }_x{T}_x/\left({\omega }_x-{\omega }_q\right)$ (1)

式中，A为地球年龄，单位：Ma (中国人常习惯用“亿年”做单位)，T_x是地史期间的某一时间点，单位：Ma，故T_x < A；ω_x是该时间点的地球自转角速度，单位：rad/s；ω_q是现今的地球自转角速度，单位：rad/s。

该式的内涵是一个地球自转速度与地球年龄增长成反比例关系的函数关系式。它设定地球惯性矩在地史期间呈线性变化，然后将其代入地球角动量守恒定律，得到地球自转速度与地球成长年龄之间的表达式为：ω_xI_x = ω_qI_q。式中，I_q为现今地球的惯性矩，I_x为地史期间某一时间点的地球惯性矩。该式显现的反比例属性来自于角动量守恒方程：因为ω_q、I_q分别为现今地球的角速度和惯性矩，它们的乘积是已知常数，即ω_xI_x = 常数。因此，地史期间的某一时间点的地球自转角速度ω_x与惯性矩I_x之间必然 成反比例关系。在地球自转的全部历史中，自转速度始终受角动量守恒方程的控制与调整。所以，将所设定的地球惯性矩成线性变化的关系式代入角动量守恒方程式时，会受到速度与惯性矩成反比例的约束。因此，(1)式作为两方程联立的结果，会依照角动量守恒定律的约束，勾画自转速度的全过程，显示时间与自转速度呈反比例变化的总趋势。当然，该反比例的描述是近似的、轮廓性的。当地球自转的初速度、太古代或元古代的某一时间点的自转速度被发现时，笔者可以改变惯性矩的设定，但最终结果仍然要建立在ω_xI_x = 常数(地球角动量守恒)之上，即建立在自转速度与新设惯性矩呈反比例函数的基础上。虽然联立了新的局部的约束条件，但是这个最基本的控制全过程的条件仍然不变，结果得到在图像上与原曲线轮廓貌似、实际近似度更高的自转速度表达式。

(1)式经变形后即成为地球自转速度表达式：

${\omega }_x=A{\omega }_q/\left(A-T_x\right),T_x<A$ (2)

式中， $A-T_x$ 可称地球的历时年龄(lasted age)，单位：Ma，是一个年龄变量。历时年龄的地质意义是：它表示从地球诞生时刻A点开始，走向今天的时间流，与由今天(图1，图2中设定为0的时间起点)走向古代A的时间流，作反向运动。两股相向的时间流在时间轴的T_x点相遇，结果等于今天的地球年龄长度，减去T_x的时间长度，留下的时间长度 $A-T_x$。它代表由A出发，走到T_x点的时间流长度，即地球的生日点到T_x点度过的时间长度，即地球已经度过的年龄。因为“地球年龄”已被特指为现今的地球年龄，为了以示区别，用“地球的历时年龄 $\left(A-T_x\right)$ ”来表达动态的地球年龄；现今地球年龄只是地球历时年龄序列中的最后一个年龄值。

本文聚焦(2)式，除上文的历时年龄 $\left(A-T_x\right)$ 的地质含义外，还将探讨以下5个问题。1) 该式是反比例函数，地球自转速度以第一象限单支双曲线形式衰减。2) 该式中T_x = A为一数学上的奇异点，及对该奇点的地质解释。3) 该单支双曲线表达的地球自转速度衰减态势，可以粗分为三大区段，列出不同的自转速度对应出现不同的地质现象。4) $\left(A-T_x\right){\omega }_x=A{\omega }_q$ = 常数的地质含义。5) 用该式预测未来某时间点的地球日长，指出未来2亿年后地球的一天可能会有25小时。

3. 地球自转速度衰减曲线

3.1. 反比例函数

地球自转速度随年龄增长成反比例衰减，其图像为位于第一象限的单支双曲线，见图1。标准型的反比例函数是： $Y=K/\left(X\pm m\right)$。式中，K为非零常数；m为双曲线图像在X轴上左右平移的单位。将它与(2)式对比，可以看到：Aω_q为大于零的常数，它相当于标准型中的K项，分母中的A相当于标准型中的m项，所以(2)式是反比例函数式。由于 ${\omega }_x>0$， $T_x>0$ (见图1)，所以(2)式的图像，为落在第一象限的反比例函数的单支双曲线。将ω轴平移至A点，ω轴、T轴是该双曲线的两条渐近线，即地球自转速度的衰减曲线。

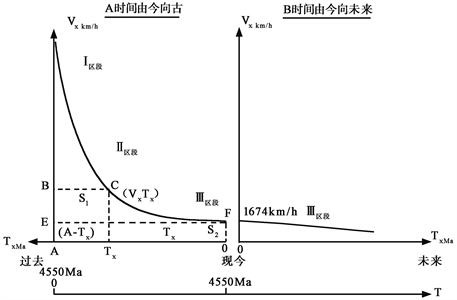
Figure 1. A schema showing attenuation of the Earth’s rotation speeds as a branch of hyperbola of an inverse proportion lying in the first quadrant

图1. 地球自转速度呈反比例函数以第一象限单支双曲线衰减的示意图

3.2. 三个减速区段

地球自转速度的衰减曲线，图1上的形态十分明显地表现为三个不同的样式，或说可划分为三个减速区段，它们是陡倾角线段、弯曲线段和缓倾角线段，对应了3个不同的地质时期。其中，占1/5地球历史 的曲线尾部，是缓倾角线段，它代表约9亿年的自转速度史，该段是可以用化石证据验证的 [2] 。其余4/5的曲线，代表约36亿年的自转速度史，这部分是目前无可验证的。但如果出现证据，比如某晚太古代的日长数据，它就可以作为检验条件，还可以作为新的约束条件，构成新的联立方程组，得到新的地球自转速度近似公式。由(2)式得到的地球自转速度半衰期序列值列于表1。表1中，V_q为现今地球自转的赤道线速度，单位：km/h；V_x为地史期间某一时间点地球自转的赤道线速度，单位同上；V_k为地球初始期的这一速度。

Table 1. Sequence of half-lifes of rotation speeds during the Earth’s history by calculating formula (2)

表1. 由(2)式计算得到的地球自转速度衰减历史中出现的速度半衰期序列表

由于不知道地球形成时的自转初速度，该半衰期序列存在系统误差。所以，表1的计算结果主要用于比较各时段速度相对的变化，推测由自转速度数量级的衰减，引起日光照长度、日温差循环扩大的可观增量，来对应同时出现的地质与古生物现象。表1取A = 4550 Ma，T_x < A回避了T_x = A的奇异端点(见下述)，从4549 Ma开始计算各地史时期地球自转速度的衰减和自转速度的半衰期。

图1中的I区段位于曲线的起始段，为陡倾角线段，其历时年龄为4542 Ma。现普遍认为地球年龄为4550 Ma，则该时段延续8 Ma。本线段的高倾角是因为时间越接近A点，线上的点越趋近渐近线，微小线段的倾角就越趋近90˚，表明该时段地球自转速度极高。计算自转速度的半衰期从4549 Ma开始，发现在该时间段内自转速度经历了三次半衰，具体结果见表1。在本区段中的三个速度半衰期都较短，时长均为百万年(Ma)的量级，其长度依次成倍增加。自转速度的衰减幅度也超级大。这一特点取决于两个因素。1) 当时地–月距离最短，地球受到月球的吸引力最大，固体潮汐的潮汐高度最高，因而地球的半径R的弹性变形大，R²的增值更大，造成惯性矩I的增量很大，因而引起自转角速度ω减速值很大，表明近地月球的引力制动作用巨大。2) 地球的初始自转速度非常高，因此自转周期超短，自转频率超高，引起的制动频率也超高。由于高值而且高频的制动力作用，使得地球高水平的初始自转速度，在其初期同时得到高水平的衰减。初步认为地球质量M的变化较小，相对于月球的引力作用，它对自转速度衰减的影响可忽略不计。

II区段位于曲线的弯曲部分，称弯曲线段，其时间跨度为4542~3526 Ma，延续长度为1016 Ma，比I区段的时间长度大2个数量级。本区段可分为2个亚段，每个亚段地球自转速度都经历三个半衰期，详见表1所列。

II区段的1亚段，时间跨度4542~4486 Ma，延续长度为56 Ma。本亚段内地球自转速度发生了3次衰减，形成三段半衰期，每段半衰期的时间长度均为10 Ma的量级。半衰期的时间长度逐次翻倍加长，曲线上的点依次逐渐偏离垂直渐近线(自转速度轴)，而向另一条水平渐近线(地质时间轴)靠近。微线段的倾角由陡逐渐变缓，微线段渐渐转向；这些微线段串联成整体即呈现为弯曲线段。

II区段的2亚段，时间跨度4486~3526 Ma，延续长度为960 Ma。它也有三段自转速度的半衰期，每个半衰期的时间长度为100 Ma的量级，比1亚段的半衰期大一个数量级。同时，地球自转速度在该亚段内也有一个量级的衰减。本亚段与I区段相比较，时长跨度的增加和自转速度的衰减都达到两个数量级的变化。椐(2)式计算，本亚段前期4422 Ma时，地球日长的40分钟约相当现今的1小时。

II区段两个亚段的两次自转速度的量级衰减，呈现在单支双曲线的图像上，是曲线的大弯曲部分。本速度衰减区段对应的重大地质现象的序列是：有水形成–出现水体–出现海洋–出现大陆。根据(2)式计算，在3788.3 Ma时自转速度衰减至10,000 km/h，越过该界点，自转速度衰减至1000 km/h的量级水平。Moody et al.认为在距今3500 Ma左右，地球上出现能够进行光合作用的兰细菌 [3] 。

需要指出：根据(2)计算，在4282 Ma时，即II区段的1亚段末期，地球赤道的自转线速度开始低于地球第一宇宙速度7.9 km/s。因此，地球表面可能有利于空气、水分逃逸的最后一扇窗户已经关闭，大气圈与水圈的似全封闭的循环条件形成。据此推断可能存留早期海洋潮汐遗迹的岩石，其年龄的最大值可能为4300 Ma。

III区段是缓倾角线段，位于该单支双曲线的中-后部。此线段展现收敛缓倾角，逐渐趋近渐近线，即趋近水平的时间轴T。其时间跨度3526~2502 Ma称a半衰期，延续1024 Ma；2502~454 Ma称b半衰期，延续2048 Ma。C半衰期则分为两个半段：其前半段从454 Ma至现今(0 Ma)，后半段(剩余的c半衰期)从现今至未来的3500 Ma，两者总共约4000 Ma。即：III区段的时间长度共计约7000 Ma，其中包括a和b两个半衰期共3072 Ma，还有c半衰期的前半段454 Ma，c半衰期剩余的后半段3500 Ma将在未来的时间中度过。现对这3个半衰期作简要说明如下。

a半衰期的时间跨度3526~2502 Ma，计算结果见表1。本半衰期的开始约在35亿年前，由于当时地球自转速度衰减而进入1000 km/h量级的大门。与此同时，地球上开始出现叠层石 [4] 。由此推测自转速度1000 km/h的量级，会引起的地球日长增加，太阳光照循环增大，昼夜差、日温差达到一个可能的临界门槛。自转速度衰减至一定的缓慢水平使得生物可以发育出明显的生长线，或者潮汐时差可发育出一定厚度的层理韵律，将自转的时钟效应记录下来。因为速度慢到一定水平，它的循环节拍可以影响有机界与无机世界；某种尺度的宏观运动，使得它们以宏观节侓来记录这种影响。这可以用这样的比喻来理解：普通相机无法拍摄高速运动，相纸上留下的影像是模糊的、不可辨认的；在低速运动的情况下，普通相机有对应的机械快门并辅以必要的光化学反应速度，可以摄下运动瞬间的清晰图像。

b半衰期的时间跨度2502~454 Ma，其延续长度比a半衰期增大一倍，达2048 Ma。它对应的地质时期是早元古代到中-晚奥陶世。因元古代位于此半衰期内，可称地球自转的“元古代半衰期”。在454 Ma时，地球的自转速度为1859.5 km/h (见表1)，它已接近于现今的地球自转速度1674 km/h，两者之间相差185.5 km/h。自转速度衰减至1859.5 km/h用了约20亿年，占地球历史全部时间长度的44%。这说明b半衰期内以微量衰减为特征，因而太阳光对地球表面的扫描速度应是平稳和缓地减慢，日循环的光照差、温度差也缓缓加大。生物以累积微量变异为主要进化手段。本半衰期内对应出现的生物演化序列是：单细胞生物–真核细胞生物–海洋生物–开始出现陆地生物。

c半衰期的时间跨度从454 Ma经过现今(0 Ma)至未来3500 Ma，时间长度约40亿年。此半衰期对应显生代以及未来的岁月，可称地球自转的“显生代半衰期”。从545 Ma开始的寒武纪是隐生代结束、显生代开始的大时代节点，生命大爆发的起始端 [3] [4] [5] 。它比c半衰期的起始端454 Ma的中–晚奥陶世早了91 Ma。比较这两个时间点的地球自转速度，由(2)式知道：545 Ma时自转速度为1901.8 km/h，454 Ma时自转速度为1859.5 km/h。可以看到：当地球自转速度衰减到1900 km/h左右时，地球的日长达到21小时，日光照的时间长度进入10¹小时量级，因此生物化学反应链条能够得到的光能、温度、时间的循环周期和梯度带的长度都有所增加，日温差水平也有跨越式的进展。本半衰期的起步与显生代的生命大爆发几乎同步。是否可以推测：c半衰期启动前后，地球自转速度大约在1900 km/h，是触发显生代到来的背景条件之一？本半衰期延续至未来的情况见图1(右)所示。

表1的算例中，如果A取4600 Ma，由(2)式得到的c半衰期，即显生代半衰期，它的开始时间点为550 Ma前，与公认的寒武纪起始点重叠。其它半衰期也仅需作同步的略微变动，即可完成表1的修改。但本文表1的A仍取4550 Ma，其原因在于：1) 学术界对地球年龄的认知，存在自4500 Ma至4600 Ma的多种方案；2) 目前尚不知道地球自转的初速度，地–月体系的形成的细节存在争议和多个假说。本文首要重视的是地球自转速度衰减的轮廓曲线，只要能够大体勾画出其总趋势即可。

4. 奇异点与地球自转行程常数

本节进一步讨论(2)式的主要特征。当T_x = A时即出现数学上的奇异点(图2)。地球自转行程常数则是地球自转速度表达式揭示的一个重要规律。

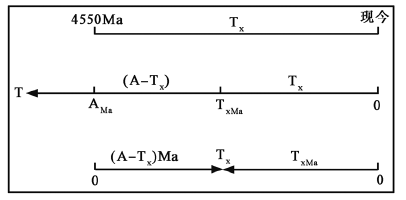
Figure 2. A schema showing the Earth’s lasted ages $\left(A-T_x\right)$ in the time coordinate axis

图2. 地球历时年龄 $\left(A-T_x\right)$ 在时间轴上的示意图

4.1. 奇异点

(2)式表明该单支双曲线的一个端点A为一孤立奇点，该奇点具有什么地质含义？当 $T_x\to A$ 时， _{${\omega }_x\to \infty$} ，在T_x = A时，分母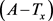为零。这意味着地球–月亮体系诞生时刻的地球，其自转的起始时刻为函数不可解的奇异点 [6] ，一个孤立的尖锐点存在于曲线的端头。对此可以有多种假说作解释。如果采用大碰撞产生月球学说：一个类火星尺度的星体碰撞原始地球，产生绕地月球。碰撞裂解爆发的瞬时即为奇异点A，此体系中的地球自转初速度瞬时爆生于该奇异点。由于太阳系的时空包容地–月系的时空，所以该奇异点具有可移动的时空条件。本文在利用(2)式计算时，据 $T_x<A$，从时间略微小于A的时刻开始计算。如果知道地–月系诞生时地球的初始自转速度，在设定地球惯性矩线性变化方程时，会增设一个常数项，导出的(2)式仍然是反比例函数，但是此时自转速度起始端为已知速度，该奇异点已被移除。这样构成的无奇异点的新(2)式的近似水平比本文的(2)式有所提高。

4.2. 地球自转行程常数

将(2)式去分母后，(2)式可改写成： $\left(A-T_x\right)V_x=A{V}_q$，式中，V_x为某地史时间点上地球自转的赤道线速度，单位：km/h；V_q为现今地球自转的赤道线速度，单位：km/h。A为现今地球年龄，一个时间点上的年龄定值； $\left(A-T_x\right)$，如前所述，为地球的历时年龄，一个随时间变化的年龄变量。

$\left(A-T_x\right)V_x=A{V}_q$ 表征：时间(地球的某历时年龄) × 速度(该年龄时的地球自转速度) = 距离(自转旋转扫过的行程)，此距离值等于现今地球年龄与现今地球自转速度之乘积(见图2)。对此可概括为：不同时代的地球年龄与该年龄时的地球自转速度之积恒为常数，其值为现今地球的此两项之积，AV_q = (45.5 × 10⁸ y) × 365 day/y × 24 h/day × 1674 km/h ≈ 6.67 × 10¹⁶ km。它表征一个特殊的地球自转扫过的长度，可以称其为“地球寿长与该寿、寿辰时自转速度的行程常数”，简称地球自转行程常数。此常数相当于上述的反比例函数中，单支双曲线下，围出的面积常量K，即反比例函数 XY = K (见图1所示)。矩形CT_xAB的面积等于矩形EFOA的面积，它们都等于常数AV_q。对此可以用这样的比喻来理解：某人发育成长停止后，25年与他25岁时的步速之积，等于35年与他35岁时的步速之积，也等于70年与他70岁时的步速之积。简言之，此人寿长与该寿、寿辰时的步速之积恒为常数。从(2)式可以看到，地球的这一特征自转行程常数除以自转速度(由化石记录的日长求取)，即得到地球的历时年龄(寿长)；地球年龄(比如已知是4550 Ma)减去地球历时年龄，得到产出化石的地层年龄 [1] 。该常数除以地球的历时年龄(由已知产出化石的地层绝对年龄和地球年龄之差取得)，得到该地层年龄时间点的地球自转速度。因该时间点的日长可知，此式也有助于化解化石生长线发育不好或者其保存不良产生的疑问 [1] 。

5. 预测未来的地球日长

按上述(1)式的思路 [2] 推导，只需改变时间轴的取向，即：将时间的流向从古代改变为向将来，其它各项符号意义不变，就能预测未来的某一时间点随地球自转速度衰减引起的地球日长变化。设地球的惯性矩随时间增加依然成线性变化，未来的地球惯性矩可表达为：

$I_x=I_q+I_q{T}_x/A$ (3)

式中各物理量的含义和单位见上文。将(3)式代入地球角动量守恒方程得到：

$A{=}_x-{\omega }_{x}T/\left({\omega }_x-{\omega }_q\right)$ (4)

该式与(1)式的形式相同，仅仅前置一个负号，表示时间的流向为向将来。如果未来地球的半径变化很小，该式中的地球自转角速度可以换成地球赤道的自转线速度，它与(2)式也是仅仅相差一个负号，该式变为 $V_x=-A{V}_q/\left(A-T_x\right)$，称(4)′式。对此可理解为：未来的地球自转速度的衰减图像，存在于图1(左)的单支双曲线的延长线上，即图1(右)。或者说，它位于地球自转速度“显生代半衰期”还没有度过的时间区段内。以下举两个实例说明运用该式预测未来的地球日长。

例一，预测2118年的地球日长。分三种情况计算，先取A = 4500 Ma。利用(4)′式可得：如果V_q = 1674 km/h，T_x = 100 y，即等于未来10⁻⁴ Ma，则有： $4500\text{Ma}=-V_x\times {10}^{-4}\text{Ma}/\left(V_x-1674\text{km}/\text{h}\right)$，V_x = 1673.9999628 km/h；故2118年的地球日长是40029.896 km/V_x = 23.9127221562 h。现今的地球日长40029.896 km/1674 km/h = 23.9127216249 h；两者相差0.00191268秒，即：2118年时地球的每一天会增长约1.91毫秒。

第二种情况，如果取A = 4550 Ma，同理得到2118年的地球日长是23.9127221504 h。与现今的地球日长相比，2118年时每天有1.89毫秒的增量。第三种情况，如果取A = 4600 Ma，同理得到2118年的地球日长是23.9127216249 h，与今天相比，每天增长1.87毫秒。取三者的平均值，在2118年时，地球每天比今天要增长1.89毫秒。

例二，预测未来哪一年，地球的日长会变成25小时。如果一天有25 h，地球赤道的线速度应为：V_x = 40029.896 km/25 h = 1601.19584 km/h。则有：A = −1601.19584 km/h × T_x/(1601.19584 − 1674) km/h = 21.9931915978 × T_x ≈ 21.9932 T_x。

按上述的计算法，如果取A = 4500 Ma，T_x = 4500 Ma/21.9932 = 204.6 Ma；如果取A = 4550 Ma，T_x = 206.9 Ma；如果取A = 4600 Ma，T_x = 209.2 Ma。取三者的平均值，说明大约在未来206.9 Ma (2.069亿年)后，地球一天的时间长度会达到25小时。

上述计算结果可与天文学家的解答大致对比。Stephenson及其合作者 [7] [8] 认为每100年地球日长的增量是1.7 ± 0.05毫秒。之后，Stephenson et al. [9] 研究计算了更多的日食资料后，认为地球每100年实际上增加约1.8毫秒；并且预测约2亿年后的地球一天会有25小时。南京大学天文系的萧耐园也认为100年后地球的一天要增长1.8毫秒 [10] 。Dickey et al. [11] 利用潮汐模型计算，认为地球日长每100年增加2.3毫秒，这个数据曾被广泛引用。由此可见：本文对未来100年后的地球日长的预测结果，处于天文研究结果和海洋潮汐研究结果之间，更接近于积累的2740年的日食资料计算得出的结果。与天文学的研究相比，两者在预测100年后地球日长的结果上，相差0.09毫秒；在预测未来地球日长达到25小时的年代方面，相差6.9 Ma (0.067亿年)。期待100年后的事实能证实我们的这些预测。