波多黎各无人机救援调度方案

Puerto Rico UAV Rescue Scheduling Scheme

摘要: 本文以2017年波多黎各遭遇飓风袭击，政府成立救助区，通过无人机来运送药物作为背景建立数学模型。为了使每个救助站获得更多的药物补给，我们首先建立了整数规划模型来寻找最优药物装箱方案；再建立TLBMCLP模型选定了集装箱的最佳放置点；通过主成分分析模型我们找到了最佳的无人机类型。最后根据所得建立多目标规划模型，优化全局效果得到最终方案。

Abstract: In this paper, a mathematical model was built based on the background of the 2017 hurricane in Puerto Rico, when the government set up rescue areas to deliver medicine by drone. To get more medicine to each station, we set up an Integer Programming Model to find the optimal drug packing scheme first. And then TLBMCLP Model was established to select the best placement point of containers. Then through the Principal Component Analysis Model, we found the best drone type. Finally, a Multi-Objective Programming Model is established to optimize the global effect and obtain the final scheme.

1. 引言

2017年，美国波多黎各领土遭受飓风“玛利亚”重创，对岛上的建筑物、房屋和道路造成了大范围的破坏，电力服务中断，通信系统被摧毁，房屋倒塌，道路阻塞。数十个地区被孤立，没有沟通，而灾区又面临医疗用品、救生设备、能量供给品的需求。不仅仅是波多黎各，在面对自然灾害频发，地面救援无法执行的情况下，制定空中灾难救援应急系统就格外重要。

波多黎各存在五个空中救援目的地，我们需使用无人机运输医疗用品。这些无人机组将建成机队，由标准集装箱运送到三个地点。

根据上述题目的背景，要求建立数学模型解决以下问题：

1) 设计一个DroneGo灾难响应系统，为每一个集装箱中设计相关的无人机装配方案。

2) 在波多黎各确定一个或多个最佳位置，用来放置三个集装箱。

3) 为无人机携带的药仓提供装箱计划并确定飞行计划。

2. 模型假设

1) 假设有无负载时飞行速度和时间保持不变

2) 假设无人机能按照预先给定路线飞行，不受其他外界因素干扰

3) 假设所有无人机的质量均相等，并且装箱存储时不会被压坏。

4) 假设无人机使用的货舱没有重量和厚度(存储在集装箱中的体积忽略不计)。

5) 假设货船沿海岸线均可停放集装箱。

3. 符号说明

4. 模型的建立

根据所涉及的问题，我们分别建立整数规划模型，TLBMCLP模型和主成分分析模型来解决上述问题，并用相应的算法来进行求解。最终建立了结合以上所有模型的多目标优化模型，来求出最优结果。具体流程如图1所示：

Figure 1. Modeling flow chart

图1. 建模流程图

4.1. 整数规划下的装箱模型 [1]

4.1.1. 约束条件与目标函数

在集装箱装载问题中，集装箱装载能力、装载利用率受多种复杂因素的约束，影响因素整理如图2所示：

Figure 2. Constraints

图2. 约束条件

根据已知条件，为使容器体积利用率达到最大，我们有目标方程为：

$\text{Max}U=\frac{\alpha \left(l_i{\omega }_i{h}_i{\beta }_i\right)}{V}+\left(1-\alpha \right){\displaystyle \sum \frac{n}{i=1}\left(\frac{g_i{\beta }_i}{G}\right)}$

根据前述所涉及的约束条件，我们得到以下约束方程：

体积约束方程：

${\displaystyle \underset{i=1}{\overset{n}{\sum }}{l}_i{\omega }_i{h}_i{\beta }_i}\le V$

重心约束方程：

$a^{\prime }\le \frac{{\displaystyle \underset{i=1}{\overset{n}{\sum }}{g}_i{x}_i{\beta }_i}}{{\displaystyle \underset{i=1}{\overset{n}{\sum }}{g}_i{\beta }_i}}\le a^{″},b^{\prime }\le \frac{{\displaystyle \underset{i=1}{\overset{n}{\sum }}{g}_i{y}_i{\beta }_i}}{{\displaystyle \underset{i=1}{\overset{n}{\sum }}{g}_i{\beta }_i}}\le b^{″},\frac{{\displaystyle \underset{i=1}{\overset{n}{\sum }}{g}_i{z}_i{\beta }_i}}{{\displaystyle \underset{i=1}{\overset{n}{\sum }}{g}_i{\beta }_i}}\le c$

其中货物重心坐标用 $\left(x_i,y_i,z_i\right)$ 表示且 $x_i\in \left[a^{\prime },a^{″}\right],y_i\in \left[b^{\prime },b^{″}\right],z_i\in \left[0,c\right]$ 。货物装载后的重心坐标边界

用 $a^{\prime },a^{″},b^{\prime },b^{″},c$ 表示。

4.1.2. 装箱模型的求解

装箱模型由于传统算法都存在收敛速度过快，易陷入局部最优解等缺陷。故我们采用改进后的智能算法 [2] 来对模型进行求解。

编码预处理：

1) 货物编号：将货物按体积由大到小降序排列， $i=1,2,3,\cdots ,n$

2) 设置方向编号：编号0代表货物不能旋转；编号1代表货物只能水平旋转；编号2代表货物能任意方向旋转。

编码及解码：

我们规定每种装载方案都对应一个编码长度为2n的符号串个体 $S_q^{gen}=\left(S_1,S_2,\cdots ,S_n,S_{n+1},\cdots ,S_{2n}\right)$ ，其中表示 $S_1~S_n$ 货物装载顺序，是由 $\left[1,n\right]$ 随机产生的一组非重复整数序列，对应序列号表示货物装载序列。 $S_{n+1}~S_{2n}$ 表示货物放置方向， $\left[0,2\right]$ 是由随机产生的一组可重复整数序列。

适应度函数：

此函数用以评价解的好坏，其值越大则解的质量越高。在此我们使用本文中的目标函数来定义适应度函数：

$\text{Max}U=\frac{\alpha \left(l_i{\omega }_i{h}_i{\beta }_i\right)}{V}+\left(1-\alpha \right){\displaystyle \sum \frac{n}{i=1}\left(\frac{g_i{\beta }_i}{G}\right)}$

根据上述算法我们用两种无人机货舱对不同类型货物进行装箱处理，所得结论如表1、表2所示：

Table 1. Drone cargo bay type 1 MED loading scheme

表1. 无人机货舱型号1装载药物方案

Table 2. Drone cargo bay type 2 MED loading scheme

表2. 无人机货舱型号2装载药物方案

我们对上述表格中较复杂情况进行分析，图3为表2方案6、7的安装方案：

Figure 3. The configuration of Plan 6/Plan 7

图3. 方案6、方案7排布方案

结合无人机载重情况可以发现，使用无人机货舱型号2时，载药量主要受载重量的影响，而并非无人机货舱体积因素影响。在使用无人机货舱型号1时，由于体积小，载药量主要受体积影响，载重量将不再影响载药量。

同时该模型不仅能用于求解药物在无人机货舱中放置问题，还能进行无人机在集装箱中的最优排布问题，使得集装箱体积得到充分利用。

4.2. TLBMCLP模型

4.2.1. 模型的概述

在本文的选址问题中，由于无人机舰队需要尽可能多地经过多条路线以勘测道路的受损情况，故属于最大覆盖选址问题(MCLP)。同时由于无人机的电量限制，故其需要在规定时间内完成任务，所以本文建立了基于时间限制的最大覆盖选址模型 [3] (TLBMCLP)。图4说明了传统的MCLP [4] 与TLBMCLP模型的区别：

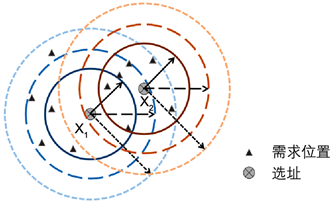
Figure 4. Traditional MCLP model and TLBMCLP model

图4. 传统的MCLP与TLBMCLP模型

给定的网络中 $G\left(V,A\right)$ ，V为顶点集， $\left|V\right|=n$ ，A为边集。 $i\in I,j\in J$ ，其中 $I\in V,J\in V$ 分别是救助点和候选停泊点的集合的下标集 $I\cup J=V$ 。 $h_i$ 为救助点i的需求量； t_ij为路网节点i接受停泊点j提供帮助的最短等待时间，也可以是两点间的最短距离表示；p为准备设立的停泊点的个数。我们希望停泊点集所能覆盖的道路节点总数达到最大。于是建立以下模型：

$\text{Max}{\displaystyle \underset{i\in I}{\sum }{\displaystyle \underset{j\in J}{\sum }{h}_i{d}_{ij}{Y}_{ij}}}$

为保证每个医院能收到至少1个集装箱的供给，得到以下约束条件：

${\displaystyle \underset{j\in J}{\sum }{Y}_{ij}}\ge 1,\forall i\in I$

为保证集装箱的个数为p个(本文中p = 3)，我们得到：

${\displaystyle \underset{j\in J}{\sum }{X}_j}=p$

通过集装箱的设立对其所供给的医院的限制，我们有：

$Y_{ij}-X_j\le 0,\forall i\in I,j\in J$

4.2.2. TLBMCLP模型的算法

对于该模型的求解，我们采用拉格朗日松弛算法 [5] ，其求解步骤为：

步骤1：初始化参数。 $k\leftarrow 1$ ， $UB\leftarrow +\infty$ ， $LB\leftarrow -\infty$ ， ${\lambda }_i^1\leftarrow \bar{h}+\frac{1}{2}\left(h_i-\bar{h}\right)\text{,}\forall i\in I$ ， ${\alpha }^k\leftarrow 2$

步骤2：根据Dijkstra算法计算，求出 $h_i{d}_{ij}\text{,}\forall i\in I,j\in J$

步骤3：寻找p个最大值的 $V_j^k\leftarrow {\displaystyle \underset{i\in I}{\sum }\max \left(0,h_i{d}_{ij}-{\lambda }_i^k\right)}$ ，将与其标号相同的 $X_j^k$ 值设为1，再通过下式求出 $Y_{ij}^k$ ，并计算上限值 $Z_U^k$

$Y_{ij}=\{\begin{array}{l}1\text{if}{X}_i=1\text{and}{h}_i{d}_{ij}-{\lambda }_i>0\\ 0\text{else}\end{array}\forall i\in I,j\in J$

步骤4：通过下式找到TLBMCLE问题的可行解，计算 $Z_L^k$

${\phi }_i=\max \left\{h_i{d}_{ij}\right\}\text{,}\forall i\in I$

步骤5：更新TLBMCLE问题的最优值的上下限UB和LB。 $UB\leftarrow \min \left(UB,Z_U^k\right)$ ， $LB\leftarrow \max \left(LB,Z_L^k\right)$

步骤6：更新步长参数 ${\alpha }^k$ ，若UB连续4次迭代都没有改善。则令 ${\alpha }^k\leftarrow {\alpha }^k/2$

步骤7：根据下式更新拉格朗日乘子

$t^k=\frac{{\alpha }^k\left(Z_U^k-LB\right)}{{\displaystyle \underset{i\in I}{\sum }{\left(1-{\displaystyle \underset{j\in J}{\sum }{Y}_{ij}^k}\right)}^2}}$ ， ${\lambda }_i^{k+1}=\max \left\{0,{\lambda }_i^k-t^k\left(1-{\displaystyle \underset{j\in J}{\sum }{Y}_{ij}^k}\right)\right\}$

步骤8：判断是否达到程序终止条件，如果下面四个条件任何一个成立则结束程序，输出结果

$\{\begin{array}{l}{\displaystyle \underset{j\in I}{\sum }{Y}_{ij}^k}=1\text{,}\forall i\in I\\ UB-LB\le 0.3\\ t^k\le 0.0001\\ k=400\end{array}$

步骤9：更新迭代次数， $k\leftarrow k+1$ ，转到第三次，

根据上述所提供的求解方案，我们可以找到最优的选址方案以覆盖更大面积，同时能保证在充足电量的情况下巡视更多的道路。

4.3. 无人机种类的选取

由于无人机种类繁多并且参数各不相同，过多的模型种类会影响模型的求解，故我们需要先对部分明显不适用的无人机或者缺点明显的无人机进行剔除。选出几种较为实用的无人机来组成舰队，以此节约运输成本并且提高工作效率。

为了选出综合评较高的无人机，我们采用主成分分析方法 [6] 。我们将从飞行距离、体积、载重、无人机货舱型号这四个因素进行综合打分。故我们根据题意整理得出以下数据，如表3所示：

Table 3. Drone performance table

表3. 无人机性能表

以上因素中，除了体积因素以外，其他因素对结论的影响都是正相关的。故为了使得求解更加准确，我们将在之后求解中对体积因素进行取负处理。同时，为避免每个因素的量纲影响结论的准确性，故我们需要将每个因素求标准分 [7] ：

其中x为原始分， $\bar{x}$ 为原始分平均值，s为原始分的标准差。通过计算各因素的标准分，我们可以得出标准分矩阵，如表4所示：

Table 4. Drone performance standard points

表4. 无人机性能标准分

根据以上矩阵，我们通过主成分分析得出了每种无人机的综合得分，并且根据无人机货舱型号和得分进行排序得到图5：

Figure 5. Score statistics

图5. 得分统计

从上表可以看出，在无人机货舱型号为1的无人机中，B、D得分较高，且可以从参数表可以看出A在各方面的性能都不及B。在B与D的比较中，我们发现B飞行距离更长，但是载重更轻。故在短距离运输时我们更倾向于采用D型无人机，而在D型无法抵达的情况时，我们采用B型无人机进行运输。

同样地，在无人机货舱型号为2的无人机中，F，E得分较高。对E和F进行比较可以发现，E体积非常小，但是飞行距离短。故无人机货舱型号为2的无人机时，若进行的运输距离短，我们更倾向于使用E无人机，否则使用F无人机。

4.4. 多目标规划模型

由于使用无人机的种类受集装箱的位置的影响，从而又会影响无人机的运载能力，进一步影响无人机的数量，再根据无人机种类和数量我们又要确定装箱方案，这是一个多目标规划问题 [8] [9] 。我们将三个集装箱所能维持各医院治疗天数为目标函数，我们将dh_i定为第i个医院所能维持的治疗天数，我们得到以下函数：

$Max\left(\underset{i\in I}{\min }d{h}_i\right)$

由于医院的维持天数受到药物分配和每日需求影响，我们得到：

$d{h}_i=\min \left[\frac{m_{ki}}{r_{ki}}\right]$

其中m_ki表示第i个医院的第k种药物的供给量，r_ki表示第i个医院的第k种药物的需求量。

现在考虑到药物分配量与集装箱到医院的距离会对无人机种类和数量的选取产生影响，我们可以得到：

$p_{ij}=f\left(m_{kj},d_i\right)$

其中f为无人机选取函数，在di较小的情况下，优先选择负载高的无人机。在di较大的情况下，优先选择飞行距离较远的无人机；p_ij为第i个医院需要第j种无人机的数量；di表示第i个医院到最近的集装箱的距离，我们有：

$d_i=\underset{j}{\min }\left\{{\left(x{h}_i-x{c}_j\right)}^2+{\left(y{h}_i-y{c}_j\right)}^2\right\}$

其中xh_i，yh_i分别为第i个医院的经纬度，xc_j，yc_j分别为第j个集装箱的经纬度.

我们还需要考虑每个集装箱的安装能力，并且求出最优安装方案。我们需要先找出每个集装箱的每类无人机数量：

$N_{kj}={\displaystyle \underset{j}{\sum }{p}_{ij}{\chi }_k(i)}$

其中N_kj为第k个集装箱的第j类无人机数量， ${\chi }_k\left(i\right)$ 为特征函数，当第j个医院接受第k个集装箱的货物时取值为1，否则为0。

根据该式求出所需无人机种类和数量，再结合装箱模型、选址模型可以得到最优的装箱、选址组合方案。使得最终结果中的无人机线路分布广，给各医院供给量多且均衡。

5. 模型的求解与分析

5.1. 问题A的解决方案

为寻找最优配置方案，根据以上所建立的模型，我们将各类无人机的参数、药物参数、集装箱的各参数以及相关地点信息代入得到以下分配方案，如表5所示：

Table 5. MED distribution and demand tables for hospitals

表5. 各医院药物分配与需求表

为了找出最优的无人机选择方案，先选取了通过主成分分析得到的四个综合得分较高的无人机B、D、E和F来进行考虑，通过加入这几类无人机相关参数和医院与集装箱的位置参数，我们得到了最优的无人机舰队组合方案，再重新代入装箱模型求取最大装入数量并寻找最优的装箱方案，我们得到了如图6所示的无人机选择方案：

Figure 6. Types and quantities of drones in each container

图6. 各集装箱无人机种类与数量

在上表中，集装箱2与集装箱3的安装方案较为复杂，在这里我们将装箱模型给出的装箱方案如图7作出：

Figure 7. The packing plan of container 2/Container 3

图7. 集装箱2、集装箱3的装箱方案

根据这一分配规则我们可以发现，由于集装箱个数的限制和无人机飞行距离的限制，我们必须尽可能地在满足距离和集装箱体积的限制下，选择运输效果更好的无人机并且同时使得装配方案又能充分利用集装箱的体积。

通过观察所得结论我们发现，在确定三个集装箱后，由于距离的限制，有些集装箱里的无人机是无法调配到距离过远的医院，因此会出现一些药物分配不均衡的情况。

根据上文提出的装配方案，我们可以由于Pavia Arecibo医院的需求量较小，故通过运输量较小的无人机B进行输送药物仍然可以给医院供给长期的药物。而HIMA医院和Caribbean医疗中心共用同一个集装箱并且离集装箱均较远，故只能采用运输性能较差而距离较远的无人机，从而导致了这两家医院的药物供给量减少，而由于这两家医院本身需求量较高，进一步使这两家医院药物维持时间减少，集装箱的供给只能维持HIMA医院使用46天，Caribbean医疗中心使用48天。

5.2. 问题B的解决方案

为解决这一问题，我们把地理因素加入到TLBMCLP模型中，其优化目标为覆盖所有的医院与道路节点。我们将主要道路的节点与医院坐标从导入MATLAB，并且根据拉格朗日松弛算法我们得到了覆盖道路节点坐标最多的地址。然后再寻找离该地址最近的沿海地点，以此来确定集装箱的停放地点。

首先，我们对已有的道路网络的信息进行提取和分析，代入TLBMCLP模型后找出最大覆盖的三个点，得到如图8：

Figure 8. Road node, hospital location and maximum coverage point

图8. 道路节点、医院位置与最大覆盖点图

求解得到最大覆盖点的相关信息，如表6所示：

Table 6. Maximum coverage point location and number of coverage points

表6. 最大覆盖点位置与覆盖数量

我们将所得到最优点代入地图中，发现属于内陆地区，而集装箱由轮船运送，故所得到的点并不贴合实际情况。我们根据地图，将所得到的点找到离其最近的沿海位置。并将其设为最优点，具体结果如图9所示：

Figure 9. Determination of container location

图9. 最终选址图

故最终确定的集装箱放置地点坐标如表7：

Table 7. Position of each container

表7. 各集装箱放置位置

结合地图可以发现，上述放置点在通往与其相邻医院时可选路线较多，无人机可以有效帮助侦查路面情况，覆盖大部分主要交通路线。并且该选点能有效保证无人机能到达预先设定的医院，且有充足电量去绕路勘测路面情况。

5.3. 问题C的解决方案

5.3.1. 无人机有效载荷包装配置

无人机打包药物受两个因素影响：1) 无人机自身载重能力；2) 无人机货舱体积的体积。在综合考虑这个问题后，我们能得出最优的无人机选择和装配方案，A问题已经给出无人机的选择和集装箱的打包方案，我们再利用考虑载重情况下的装箱模型和各医院的需求来确定无人机的药物打包方案。利用优化的遗传算法，我们通过MATLAB求解得到结论，整理成表8：

Table 8. Program for MED packaging

表8. 药物打包方案

我们发现大多数医院都只收到一个集装箱的补给，但是Puerto Rico儿童医院同时收到集装箱1和集装箱2的补给，由于集装箱2附近的两个医院需求量高，而集装箱2的药物存量有限。故求解发现Puerto Rico 儿童医院还可以从集装箱1获得药物补给，并且集装箱1供应的Pavia Arecibo医院本身需求量较小，所以Puerto Rico儿童医院又可以接受集装箱1的供给。故我们得到了该医院接受集装箱1时使用B型无人机，数量为46台；接受集装箱2时使用F型无人机，数量为30台。

对于集装箱3所供给的两所医院，这两所医院本身距离较为偏僻，无法接受其他两个集装箱的供给，导致资源较少，使得这两个医院最终分配到的药物只能使用46天和48天，几乎只是其他医院使用天数的一半。

5.3.2. 无人机飞行计划和时间表

依照前文所得的各集装箱运往各医院的无人机种类和数量，我们根据最大覆盖法求解得出多条线路，并且在这些线路内无人机都能保证有充足电量。在海拔较高的地方设置海拔高度，使得无人机进行绕行 [10] 。对模型求解我们得到大量可用路线数据，以下我们给出含有每个方向的几条典型路线的图片，如图10所示：

Figure 10. The roadmap

图10. 路线图

根据所得出的路线，我们对每条路线的距离进行计算，并且根据该路线使用无人机类型的飞行速度，我们对其行驶时间进行了计算，得到表9所示结论：

Table 9. Route schedule

表9. 各路线时间表

根据上述表格我们发现各路线的飞行时间均在无人机的最大飞行时长内，模型求解准确有效。并且基本都保证了充分利用无人机的电量去巡视更多的道路，以便用来最终评估道路受损情况。