体积勾股定理的证明

The Proof of Volume Pythagorean Theorem

摘要:

用Cayley-Menger行列式证明：当四面体满足“对棱相等、或对棱的平方和相等”时，存在体积勾股定理：“该四面体的体积的平方等于所围的四个面外凸的直角四面体体积的平方和”，其公式为：V²_ABCD=V²_ABC4+V²_ABD3+V²_ACD2+V²_BCD1(标注见：图1)。

Abstract: The Cayley-Menger determinant  is used to prove that when the tetrahedron satisfies “The same of opposite sides respective, or The same of the sum of squares of opposite sides”, there exists The Volume Pythagorean Theorem: “the square of the volume of the tetrahedron is equal to the sum of squares of the volumes of the four Right Angle Tetrahedrons by Surrounded by external”. The formula is:V²_ABCD=V²_ABC4+V²_ABD3+V²_ACD2+V²_BCD1 (the label is shown in Figure 1).

1. 引言

1) 已知勾股定理：直角三角形的2条直角边的平方和等于斜边的平方。其公式：

$a^2+b^2=c^2$

2) 已知面积勾股定理 [2] ：直角四面体的3个直角三角形面积的平方和等于斜面锐角三角形面积的平方：其公式：

$S_{\Delta ABC}^2=\frac{1}{4}\left(a^2{b}^2+a^2{c}^2+b^2{c}^2\right)$

3) 问题提出：是否可推广至“体积勾股定理”？

2. 体积勾股定理的证明

2.1. 体积勾股定理

当四面体的3组对棱分别相等、或3组对棱的平方和相等，该四面体体积的平方等于其4个三角面外凸直角四面体体积的平方和。其公式为：

$V_{ABCD}^2=v_{ABC4}^2+v_{ABD3}^2+v_{ACD2}^2+v_{BCD1}^2=\frac{1}{36}\left(a^2{b}^2{c}^2+a^2{b}^2{d}^2+a^2{c}^2{d}^2+b^2{c}^2{d}^2\right)$ (1)

注：下标： $A,B,C,D$ 为四面体的4顶点，1，2，3，4为外凸4个直角四面体的直角的交点(见图1)。

Figure 1. Four right-angled tetrahedrons outside Tetrahedrons

图1. 四面体外4个直角四面体图

2.2. 证明

根据Cayley-Menger行列式四面体体积公式 [1] 即：任意四面体给定4顶点间距离，求四面体体积的平方公式为：

$V_{1234}^2=\frac{1}{288}\left|\begin{array}{ccccc}0& 1& 1& 1& 1\\ 1& 0& d_{12}^2& d_{13}^2& d_{14}^2\\ 1& d_{12}^2& 0& d_{23}^2& d_{24}^2\\ 1& d_{13}^2& d_{23}^2& 0& d_{34}^2\\ 1& d_{14}^2& d_{24}^2& d_{34}^2& 0\end{array}\right|$ (2)

下标 $ij\in 1,2,3,4$ 表示四面体4顶点， $d_{ij}$ 是连接两个顶点连线的长度。

2.2.1. 所设如(图1)

· 设四面体4顶点为： $A,B,C,D$ ；

· 设公式(2)四面体各顶点间距离为：

$a=d_{23};b=d_{13};c=d_{12};d=d_{14};e=d_{24};f=d_{34}$

注： $\left(a,b,c\right)$ 的对棱依次为 $\left(d,e,f\right)$ 。

· 设外凸4个直角四面体的直角交点为：1、2、3、4点(依次为四面体( $A,B,C,D$ ) 4顶点的对平面的凸点)，及其至四面体各顶点距离设为(参见：图1)：

$\begin{array}{l}A4=a_4,B4=b_4,C4=c_4,A3=a_3,B3=b_3,D3=d_3,\\ A2=a_2,C2=c_2,D2=d_2,B1=b_1,C1=c_1,D1=d_1,\end{array}$

2.2.2. 证明

假设公式(1)成立，公式(2)转换成公式(3)所设体积的平方和，联立公式为：

$\begin{array}{c}{V}_{ABCD}^2=\frac{1}{288}\left|\begin{array}{ccccc}0& 1& 1& 1& 1\\ 1& 0& c^2& b^2& d^2\\ 1& c^2& 0& a^2& e^2\\ 1& b^2& a^2& 0& f^2\\ 1& d^2& e^2& f^2& 0\end{array}\right|\\ =\frac{1}{36}\left(a_4^2{b}_4^2{c}_4^2+a_3^2{b}_3^2{d}_3^2+a_2^2{c}_2^2{d}_2^2+b_1^2{c}_1^2{d}_1^2\right)\end{array}$ (3)

将公式(3)右侧的4个直角四面体体积的平方，根据勾股定理，再转换成所设的四面体的6棱 $\left(a,b,c,d,e,f\right)$ 来表达：使得公式(3)左右式统一计量。表达式为：

$\{\begin{array}{l}\frac{1}{36}{a}_4^2{b}_4^2{c}_4^2=\frac{1}{36}\frac{-a^2+b^2+c^2}{2}\frac{a^2-b^2+c^2}{2}\frac{a^2+b^2-c^2}{2}\\ \frac{1}{36}{a}_3^2{b}_3^2{d}_3^2=\frac{1}{36}\frac{c^2+d^2-e^2}{2}\frac{c^2-d^2+e^2}{2}\frac{-c^2+d^2+e^2}{2}\\ \frac{1}{36}{a}_2^2{c}_2^2{d}_2^2=\frac{1}{36}\frac{b^2+d^2-f^2}{2}\frac{b^2-d^2+f^2}{2}\frac{-b^2+d^2+f^2}{2}\\ \frac{1}{36}{b}_1^2{c}_1^2{d}_1^2=\frac{1}{36}\frac{a^2+e^2-f^2}{2}\frac{a^2-e^2+f^2}{2}\frac{-a^2+e^2+f^2}{2}\end{array}$ (4)

将公式(4)右式代入公式(3)右式，合并系数，假设等式成立，公式(3)左右式之差为零。计算结果为：

$\begin{array}{c}0=\frac{1}{288}\left|\begin{array}{ccccc}0& 1& 1& 1& 1\\ 1& 0& c^2& b^2& d^2\\ 1& c^2& 0& a^2& e^2\\ 1& b^2& a^2& 0& f^2\\ 1& d^2& e^2& f^2& 0\end{array}\right|\\ -\frac{1}{288}[\left(-a^2+b^2+c^2\right)\left(a^2-b^2+c^2\right)\left(a^2+b^2-c^2\right)\\ +\left(c^2+d^2-e^2\right)\left(c^2-d^2+e^2\right)\left(-c^2+d^2+e^2\right)\\ +\left(b^2+d^2-f^2\right)\left(b^2-d^2+f^2\right)\left(-b^2+d^2+f^2\right)\\ +\left(a^2+e^2-f^2\right)\left(a^2-e^2+f^2\right)\left(-a^2+e^2+f^2\right)]\end{array}$

展开整理后为：

$\begin{array}{l}\Rightarrow 0={\left(a^2-d^2\right)}^2\left(2a^2+2d^2-b^2-c^2-e^2-f^2\right)\\ +{\left(b^2-e^2\right)}^2\left(2b^2+2e^2-a^2-c^2-d^2-f^2\right)\\ +{\left(c^2-f^2\right)}^2\left(2c^2+2f^2-a^2-b^2-d^2-e^2\right)\end{array}$ (5)

2.2.3. 根据公式(5)得

体积勾股定理成立的2个条件为：公式(5)的3组2项乘积，其中：3组前项均为零，或3组后项均为零(含前后项同时均为零)。

· 条件一：3组前项均为零时：3组对棱分别相等。

$0=\{\begin{array}{l}\left(a^2-d^2\right)\\ \left(b^2-e^2\right)\\ \left(c^2-f^2\right)\end{array}\Rightarrow \{\begin{array}{l}a=d\\ b=e\\ c=f\end{array}$ (6)

· 条件二：3组后项同时为零时：3组对棱的平方和相等。

$\begin{array}{c}0=\{\begin{array}{l}\left(2a^2+2d^2-b^2-c^2-e^2-f^2\right)\\ \left(2b^2+2e^2-a^2-c^2-d^2-f^2\right)\\ \left(2c^2+2f^2-a^2-b^2-d^2-e^2\right)\end{array}\Rightarrow \{\begin{array}{l}2\left(a^2+d^2\right)=b^2+c^2+e^2+f^2\\ 2\left(b^2+e^2\right)=a^2+c^2+d^2+f^2\\ 2\left(c^2+f^2\right)=a^2+b^2+d^2+e^2\end{array}\\ \Rightarrow \left(a^2+d^2\right)=\left(b^2+e^2\right)=\left(c^2+f^2\right)\end{array}$

2.2.4. 结论

当四面体满足3组对棱分别相等、或3组对棱的平方和相等时。公式(3)及其体积勾股定理成立。命题得证。

2.3. 验证及引理

2.3.1. 验证条件一

当四面体的3组对棱分别相等：其体积公式可转化为：

$V_{ABCD}^2={\left[xyz-4\left(\frac{1}{6}xyz\right)\right]}^2={\left(\frac{1}{3}xyz\right)}^2=4{\left(\frac{1}{6}xyz\right)}^2$ (7)

验证毕。

· 引理1：四面体3组对棱分别相等时，其组合体为矩形，且3组对棱分别平行的体积勾股定理。因仅见3维，简称为：3维平行体积勾股定理(见图2)。

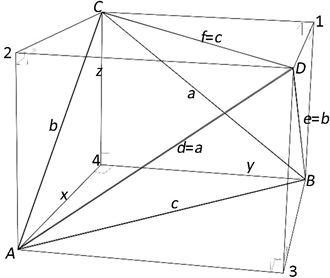
Figure 2. The three pairs of edges are identical respectively

图2. 三组对棱分别相等图

2.3.2. 验证条件二

当四面体的3组对棱平方和相等：为4球正交，其6棱的体积公式(3)可转化为4球半径为 $x,y,z,w$ 的正交4球心间体积勾股定理公式(见：图3)：

Figure 3. Orthogonal 4-sphere graph

图3. 正交4球图

$\begin{array}{c}{V}_{xyzw}^2=\frac{1}{288}\left|\begin{array}{ccccc}0& 1& 1& 1& 1\\ 1& 0& x^2+y^2& x^2+z^2& x^2+w^2\\ 1& x^2+y^2& 0& y^2+z^2& y^2+w^2\\ 1& x^2+z^2& y^2+z^2& 0& z^2+w^2\\ 1& x^2+w^2& y^2+w^2& z^2+w^2& 0\end{array}\right|\\ =\frac{1}{36}\left(x^2{y}^2{z}^2+x^2{y}^2{w}^2+x^2{z}^2{w}^2+y^2{z}^2{w}^2\right)\end{array}$ (8)

· 公式(3) 6棱 $a,b,c,d,e,f$ 与公式(8) 4球半径 $x,y,z,w$ 对应关系(左式)为：

$\begin{array}{l}{a}^2=y^2+z^2,b^2=x^2+z^2,c^2=x^2+y^2,\\ d^2=x^2+w^2,e^2=y^2+w^2,f^2=z^2+w^2,\end{array}$

$a^2+d^2=b^2+e^2=c^2+f^2=x^2+y^2+z^2+w^2$ (3组对棱的平方和相等)

· 四面体4顶点与外凸交点间连线，公式(3)右式等于公式(8)右式。即证明：

$\left(a_4^2{b}_4^2{c}_4^2+a_3^2{b}_3^2{d}_3^2+a_2^2{c}_2^2{d}_2^2+b_1^2{c}_1^2{d}_1^2\right)=\left(x^2{y}^2{z}^2+x^2{y}^2{w}^2+x^2{z}^2{w}^2+y^2{z}^2{w}^2\right)$

根据垂心四面体对棱的平方和相等关系可证：

$x^2=\{\begin{array}{l}{a}_4^2=\frac{b^2+c^2-a^2}{2}\\ a_3^2=\frac{c^2+d^2-e^2}{2}\\ a_2^2=\frac{b^2+d^2-f^2}{2}\end{array}$ 代入所设 $\Rightarrow x^2=\{\begin{array}{l}{a}_4^2=\frac{x^2+z^2+x^2+y^2-y^2-z^2}{2}\\ a_3^2=\frac{x^2+y^2+x^2+w^2-y^2-w^2}{2}\\ a_2^2=\frac{x^2+z^2+x^2+w^2-z^2-w^2}{2}\end{array}$

$y^2=\{\begin{array}{l}{b}_4^2=\frac{a^2+c^2-b^2}{2}\\ b_3^2=\frac{c^2+e^2-d^2}{2}\\ b_1^2=\frac{a^2+e^2-f^2}{2}\end{array}$ 代入所设 $\Rightarrow y^2=\{\begin{array}{l}{b}_4^2=\frac{y^2+z^2+x^2+y^2-x^2-z^2}{2}\\ b_3^2=\frac{x^2+y^2+y^2+w^2-x^2-w^2}{2}\\ b_1^2=\frac{y^2+z^2+y^2+w^2-z^2-w^2}{2}\end{array}$

$z^2=\{\begin{array}{l}{z}_4^2=\frac{a^2+b^2-c^2}{2}\\ z_2^2=\frac{b^2+f^2-d^2}{2}\\ z_1^2=\frac{a^2+f^2-e^2}{2}\end{array}$ 代入所设 $\Rightarrow z^2=\{\begin{array}{l}{z}_4^2=\frac{y^2+z^2+x^2+z^2-x^2-y^2}{2}\\ z_2^2=\frac{x^2+z^2+z^2+w^2-x^2-w^2}{2}\\ z_1^2=\frac{y^2+z^2+z^2+w^2-x^2-w^2}{2}\end{array}$

$w^2=\{\begin{array}{l}{d}_3^2=\frac{d^2+e^2-c^2}{2}\\ d_2^2=\frac{d^2+f^2-b^2}{2}\\ d_1^2=\frac{e^2+f^2-a^2}{2}\end{array}$ 代入所设 $\Rightarrow w^2=\{\begin{array}{l}{d}_3^2=\frac{x^2+w^2+y^2+w^2-x^2-y^2}{2}\\ d_2^2=\frac{x^2+w^2+z^2+w^2-x^2-z^2}{2}\\ d_1^2=\frac{y^2+w^2+z^2+w^2-y^2-z^2}{2}\end{array}$

因此，公式(8)得以验证。且得出：

· 引理2：四面体3组对棱的平方和相等时，其形态为正交4球的多胞体，外凸4交点为不同的3球面交点，且4球心连线对棱垂直，其所围体积的平方等于4个3球心与外凸球面交点所围体积的平方和的体积勾股定理。可见正交4球半径，简称为：4维垂直体积勾股定理。

2.3.3. 验证同时满足上述2条件的特例

验证当同时满足上述2条件的交集特例，即矩形体积的3边均相同为a时，为正方体、也是正交4球的半径均相同为x时，为正四面体。两者均仅存单变量。对棱既平行同时又垂直。

· 四面体棱与正交4球半径关系为 $2a^2=2x^2\Rightarrow a=x$ ：

$V_{xyzw}^2=\frac{1}{288}\left|\begin{array}{ccccc}0& 1& 1& 1& 1\\ 1& 0& 2a^2& 2a^2& 2a^2\\ 1& 2a^2& 0& 2a^2& 2a^2\\ 1& 2a^2& 2a^2& 0& 2a^2\\ 1& 2a^2& 2a^2& 2a^2& 0\end{array}\right|=\frac{8a^6}{9}=\frac{1}{288}\left|\begin{array}{ccccc}0& 1& 1& 1& 1\\ 1& 0& 2x^2& 2x^2& 2x^2\\ 1& 2x^2& 0& 2x^2& 2x^2\\ 1& 2x^2& 2x^2& 0& 2x^2\\ 1& 2x^2& 2x^2& 2x^2& 0\end{array}\right|=\frac{8x^6}{9}$

· 引理3：当6棱全等时，同时满足上述两条件，且仅见单变量，简称为：正体积勾股定理。

验证及引理毕。

3. 总结

3.1. 当四面体对棱分别相等

存在“对棱平行为矩形的三维体积勾股定理”。其4面体体积的平方等于外围4个相同的直角四面体体积的平方和(含6棱全等的特例)，这里仅见的3维也可约去，公式可简化为：

${\left(\frac{1}{3}\right)}^2={\left(\frac{1}{6}\right)}^2+{\left(\frac{1}{6}\right)}^2+{\left(\frac{1}{6}\right)}^2+{\left(\frac{1}{6}\right)}^2=\frac{1}{9}.$

3.2. 当四面体3组对棱的平方和相等

存在“正交4球心间对棱垂直的四维体积勾股定理”。其特征正交4球心间体积的平方等于四组3球心与球面交点构成的直角四面体体积的平方和(含6棱全等的特例)。

特别是“四球正交体积勾股定理”的新发现，对正交4球(含垂心四面体)，在3D坐标系中，建立坐标、多项式的化简、计算相关几何参数和分析有了新的计算工具。