1. 引言
随着视觉跟踪运动控制系统的广泛应用,提高视觉反馈的实时性已经成为进一步扩展此类系统应用的关键技术之一 [1] 。这些应用所需的一种技术是视觉伺服,其定义是根据从视觉传感器收集的信息来控制机构。视觉伺服的一个基本任务是跟踪通过空间移动的对象,假设目标的运动是两个连续帧之间的小位移,因此可以在最后帧中找到对象的区域中搜索对象。因为只需考虑物体在两个框架之间的相对位移,所以视觉伺服的优点在于简化了由视觉传感器传送的数据的处理流程。用主动摄像机跟踪物体的任务包括两个主要主题:视觉处理和控制理论。本文将讨论第二个主题,重点讨论具有活动末端执行器的对象。从控制理论的角度看,需要解决三大难题。主要的困难是图像采集和处理所需时间的延迟。第二个困难是典型的噪声信号。第三个困难是由传感器的帧速率引入的采样速率的限制 [2] 。
克服视觉传感器引入的延迟的一个常见方法是使用预测算法。卡尔曼滤波是一种常用的目标预测算法,针对不同的预测条件,延伸出了扩展卡尔曼滤波 [3] [4] [5] 、自适应卡尔曼滤波 [6] [7] [8] [9] 等多种形式。Corke在 [10] 中提出了考虑视觉传感器延迟的控制方案,将卡尔曼滤波器预测得到信息使用在控制器之后,这不利于使用当前时刻的预测值控制机器人运动。本文在其基础上,提出了一种新的预测方案,将控制系统中的卡尔曼滤波器设置在运动控制器之前,从而使控制器获得当前时刻的跟踪目标位置信息,进而减小控制机器人运动的任务函数的幅值。通过引入预测监视器来最小化由于依赖于估计而导致的跟踪误差。预测监视器的任务是监督预测误差,并判断这个误差是否表示目标运动中的不连续性。由于没有实际目标轨迹的信息,只能使用视觉传感器的测量。因此,预测监视器必须处理由于典型噪声的视觉数据而导致的预测质量的下降,并且只对目标运动的实际不连续性作出反应。如果预测监视器检测到不连续,则重新初始化预测器,辅助控制器设置控制律以防止大超调。
2. 控制方案说明
在经典的控制方案文献 [10] 的基础上,本文提出了如图1所示的视觉伺服控制方案。在本方案中机器人离散模型用
表示,视觉系统用
表示,其通常被建模为一个纯延迟
。其中
是将目标姿态与图像平面相关联的增益。模块KF是自适应卡尔曼滤波器,用于估计当前的目标位置
。模块
表示机器人控制器,它将最大限度地减小 (目标位置
(目标位置 与机器人位置
与机器人位置 之间的差的数值)。低水平的连续机器人模型
之间的差的数值)。低水平的连续机器人模型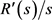 由机器人的惯性和执行机构的动力学构成,采用经典单元负反馈的低水平动态控制器D(Z)对机器人块R(Z)进行控制。使用测速计M(z)计算机器人速度
由机器人的惯性和执行机构的动力学构成,采用经典单元负反馈的低水平动态控制器D(Z)对机器人块R(Z)进行控制。使用测速计M(z)计算机器人速度 ,其中
,其中 由编码器处离散获得。为了在连续信号和离散信号之间进行转换,在系统中设置了两个零阶保持器(ZOH)。
由编码器处离散获得。为了在连续信号和离散信号之间进行转换,在系统中设置了两个零阶保持器(ZOH)。
图1的控制方案中的一个重要改进是卡尔曼滤波器输出当前机器人位置 进入三个控制回路,实时反映视觉系统中的图像特征的实际差值,减小在基准配对过程中存在的视野丢失的概率;为第1级卡尔曼滤波器的预测工作减小误差,使其结果有效收敛;任务函数法中的
进入三个控制回路,实时反映视觉系统中的图像特征的实际差值,减小在基准配对过程中存在的视野丢失的概率;为第1级卡尔曼滤波器的预测工作减小误差,使其结果有效收敛;任务函数法中的 更快趋近于0,并保证其控制过程中不会因为延迟导致过大的超调。自适应卡尔曼滤波器输出的是经过两次预测的数据,保证其预测的目标位置的
更快趋近于0,并保证其控制过程中不会因为延迟导致过大的超调。自适应卡尔曼滤波器输出的是经过两次预测的数据,保证其预测的目标位置的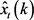 是当前时刻k的值而不是前一时刻k − 1的值。
是当前时刻k的值而不是前一时刻k − 1的值。
3. 滤波器设计
考虑如下非线性系统的状态估计问题:
 (1)
(1)
 (2)
(2)
式中:状态向量 ,输出向量
,输出向量 ;矩阵
;矩阵 是所谓的系统矩阵,它描述状态从
是所谓的系统矩阵,它描述状态从 到k时刻的传播;
到k时刻的传播;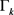 为k时刻的系统噪声矩阵;矩阵
为k时刻的系统噪声矩阵;矩阵 描述从状态x生成测量值的矩阵;
描述从状态x生成测量值的矩阵; 是系统的状态噪声序列,
是系统的状态噪声序列, 是测量噪声序列,假设噪声序列为高斯序列、白序列和无关的,并具有如下统计特征:
是测量噪声序列,假设噪声序列为高斯序列、白序列和无关的,并具有如下统计特征: ,
, ,
,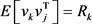 ,
,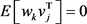 。其中
。其中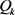 为对称非负定矩阵,
为对称非负定矩阵, 为对称正定矩阵。初始状态
为对称正定矩阵。初始状态 为高斯分布的随机向量,且与
为高斯分布的随机向量,且与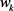 、
、 统计独立。
统计独立。
由式(2)可知,预测与当前时刻的状态有关外,还与前一时刻的状态有关,即预测方程为状态的n阶延迟,为了解决此类系统的状态估计问题,在文献 [6] EKF的基础上提出了延迟算法,AKF的迭代过程如式(3)~(9)所示。
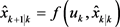 (3)
(3)
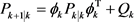 (4)
(4)
 (5)
(5)
 (6)
(6)
 (7)
(7)
 (8)
(8)
 (9)
(9)
在视觉伺服跟踪条件下,矩阵 和
和 分别取值为
分别取值为
 ,
,
其中T为采样时间,欲使上述算法具有强跟踪特性,则应该满足如下正交性原理:
 (10)
(10)
 (11)
(11)
利用上述正交性原理,令 ,若
,若 成立,则有下式:
成立,则有下式:
 (12)
(12)
式中:
 (13)
(13)
欲使上述正交性原理成立,通过将式(12)转换成选择适当的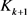 ,使下式成立。
,使下式成立。
 (14)
(14)
其中残差协方差矩阵 可由下式估计得到:
可由下式估计得到:
 (15)
(15)
式中 为遗忘因子,将式(6)中的
为遗忘因子,将式(6)中的 代入式(14)后可得:
代入式(14)后可得:
 (16)
(16)
采用自适应渐消因子对上一时刻数据渐消,实时调整状态预测误差协方差矩阵以及相应的增益矩阵,从而削弱上一时刻数据对当前估计值的影响。于是,修改式(4)中的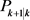 为
为
 (17)
(17)
式中: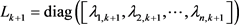 为渐消矩阵;
为渐消矩阵; 为渐消因子。由系统的先验知识确定
为渐消因子。由系统的先验知识确定 。令
。令 。其中,
。其中, 为预先确定的常数;
为预先确定的常数; 为待定因子。则渐消因子由下式得到:
为待定因子。则渐消因子由下式得到:
 (18)
(18)
将式(17)代入式(16)可得:
 (19)
(19)
式中β为弱化因子,对上式求迹可得:
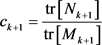 (20)
(20)
式中:
 (21)
(21)
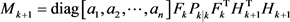 (22)
(22)
上述即为AKF的递推过程,结合视觉伺服系统建立联合状态估计算法,步骤如下:
1) 令 ,初始化机器人的初始状态
,初始化机器人的初始状态 ,状态预测误差协方差矩阵
,状态预测误差协方差矩阵 ,噪声协方差矩阵Q、R以及参数
,噪声协方差矩阵Q、R以及参数 、
、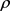 、
、 ,由于两个滤波器在同一条件下进行工作,故将参数设置成相同的值。
,由于两个滤波器在同一条件下进行工作,故将参数设置成相同的值。
2) 由式(3)、(8)分别计算出 ,
, 以及系数矩阵
以及系数矩阵 、
、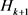 、
、 。
。
3) 由式(15)计算出 ,联合式(18)、(20)计算出渐消矩阵
,联合式(18)、(20)计算出渐消矩阵 。
。
4) 由式(17)计算出 ,由式(5)、(6)计算
,由式(5)、(6)计算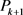 ,
,
5) 由式(9)、(7)分别更新状态估计 和误差协方差矩阵
和误差协方差矩阵 。
。
通过上述步骤估计得到k时刻的目标位置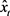 。
。
4. 预测监视器
预测监视器PM是检测目标运动中不连续性的一种算法。如果位置、速度或加速度信号变化率足够大,则可以称为一个阶跃,并认为该运动是不连续性的。对于PM来说,快速检测不连续是很重要的,因为延迟的重新初始化会产生比不重新初始化更差的结果。为了说明这一要求,由图2表示步长变化条件下的积分绝对平均误差,并在步骤发生后的t秒内重新初始化AKF。可以看出,如果不能快速反应,当IAM值超过AKF值时,不需要由水平线重新初始化。PM的另一个要求是对噪音不敏感,这意味着PM应该区分由噪声产生的预测误差和由于目标的不连续性运动而产生的误差。
 (23)
(23)
PM的结构如图3所示。其中 定义了允许的预测误差带的宽度,而
定义了允许的预测误差带的宽度,而 是这个误差带的中心。
是这个误差带的中心。
 定义的两步预测误差为:
定义的两步预测误差为:
 (24)
(24)
其中 是实际的测量值,
是实际的测量值, 是从时间瞬态的k − 2到k的两步预测。为了适应环境或运动中的变化,这两项都不应该引起PM的反应,
是从时间瞬态的k − 2到k的两步预测。为了适应环境或运动中的变化,这两项都不应该引起PM的反应, 和
和 必须在线进行调整。
必须在线进行调整。
一种常见的检测机动目标突然变化的方法是使用马氏距离:
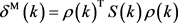 (25)
(25)
如果滤波器的模型符合实际系统,则式(25)定义的新息序列的均值为零。为了判断测量的准确性,需要对误差带进行调整。例如,当目标在正弦轨迹上运动时,假设加速度不恒定,则预测误差为噪声测量和模型误差之和。使用最后n个预测误差序列的标准差来进行误差带的适配:
 (26)
(26)
其中 为序列的平均值。误差带由式(27)确定:
为序列的平均值。误差带由式(27)确定:
 (27)
(27)
其中 是一个固定常数。因为平均值对动态信号的适应太慢,所以波段的中心将使用低通滤波器
是一个固定常数。因为平均值对动态信号的适应太慢,所以波段的中心将使用低通滤波器
 ,而不是
,而不是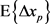 来调整。
来调整。
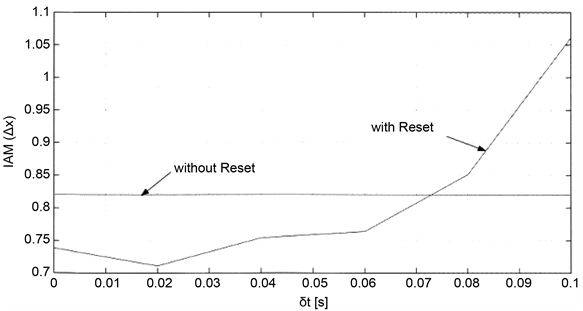
Figure 2. IAM values after PM performs initialization
图2. PM执行初始化后的IAM值
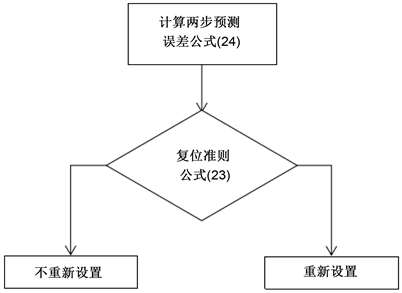
Figure 3. Structure of predictive monitor PM
图3. 预测监视器PM的结构
5. 仿真实验与结果分析
如图4所示,设计一个目标由静止状态并突然开始做正弦运动的仿真实验。本实验是通过将目标安装在旋转的杆上实现的,目标在一个周期3 s内完成加减速运动,振幅为x = 2m。通过本文提出的视觉伺服方案,对图4所示的运动目标进行仿真测试之后,得到如图5所示的仿真结果。由图5看出,误差一开始呈指数递减,在到达减速–加速阶段时出现短暂误差增大,其后又保持平稳,说明该控制系统具有较好的鲁棒性。通过对比图5(a)和图5(b)可以看出,增大采样时间Th,可以有效减小因减速–加速阶段引起的不稳定性。说明本系统作为一种强跟踪性质的滤波算法,能有效跟踪目标状态的突变和扰动。实际系统存在噪声,算法通过在线变化渐消因子来抵消噪声的影响,使稳态估计准确平稳,具有很强的噪声抑制能力。
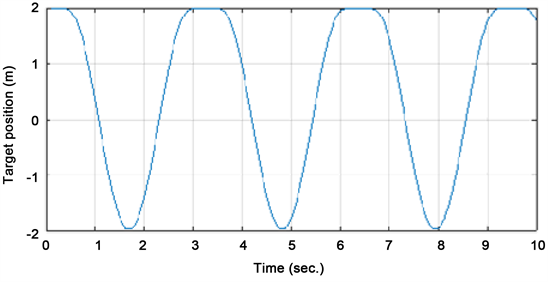
Figure 4. Shows the tracking target of acceleration and deceleration motion
图4. 做加减速运动的跟踪目标
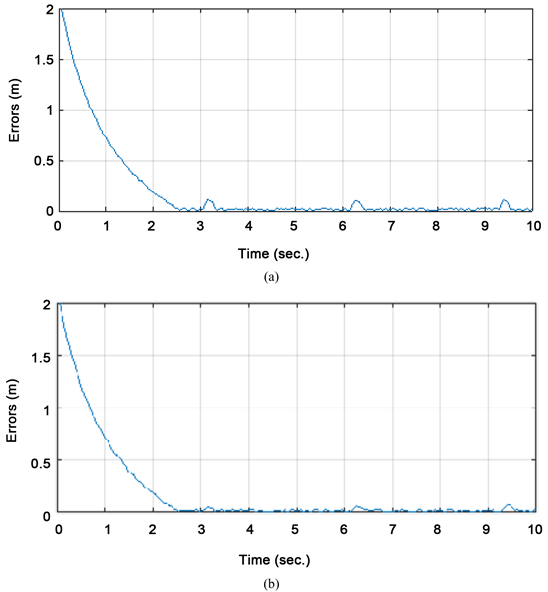
Figure 5. (a) Th = 0.04 sec; Th = 0.002 sec
图5. (a) Th = 0.04 sec;Th = 0.002 sec
6. 结论
本文的主要任务是开发一种用于跟踪不连续运动目标的视觉伺服方案。为提高视觉伺服系统的跟踪速度,提供了良好的平滑和间断运动预测质量。该方案使用自适应卡尔曼滤波器预测下一时刻的目标位置,减小运动控制器中由于系统延迟而导致的误差。PM连续地监视预测质量,并且在检测到不连续时将重新初始化脉冲发送到滤波器。在正弦运动的实验中分析了所提出方案的性能,图像平面误差都得到了显著的减小,系统表现出快速的反应以及几乎消除了过冲。未来的工作需要进一步改善PM的行为,以增加它对在平滑运动中产生脉冲的不连续运动的敏感性。
基金项目
国家自然基金(61803186);江苏省研究生科研与实践创新计划项目(SJCX18_1052)。
NOTES
*通讯作者。