基于回归分析的城镇化发展对生态环境影响的研究——以Z市为例

Study on the Impact of Urbanization on Ecological Environment Based on Regression Analysis—Taking Z City as an Example

摘要: 城镇化发展是衡量一个地区综合实力的重要因素，同时生态环境与人们的生产生活有着密不可分的关系。为研究城镇化发展对生态环境的影响，本文选取Z市相关数据，构建城镇化、生态环境指标体系，以城镇化发展相关指标为自变量，通过熵权法将生态环境有关的多个指标综合为因变量，运用R软件分析所获得的样本数据，通过逐步回归法建立多元回归方程。分析结果表明：人均生产总值等因素对生态环境正向影响显著，民用汽车拥有量对生态环境负向显著影响。基于上述分析结果，本文从人口、经济、社会等三方面对城镇化发展提出合理化意见，进而促进生态环境与城镇化和谐发展。

Abstract: The development of urbanization is an important factor to measure the comprehensive strength of a region. At the same time, the ecological environment is inextricably linked with people’s pro-duction and life. In order to study the impact of urbanization development on the ecological envi-ronment, this paper selects the relevant data of Z city, constructs the urbanization and ecological environment index system, takes the relevant indicators of urbanization development as the in-dependent variables, and integrates multiple indicators related to the ecological environment through the entropy method. For the dependent variable, R software was used to analyze the sam-ple data obtained, and the multiple regression equation was established by stepwise regression method. The analysis results show that factors such as per capita GDP have a positive impact on the ecological environment, and the amount of civilian vehicles has a negative impact on the ecological environment. Based on the above analysis results, this paper proposes rationalization opinions on urbanization development from the three aspects of population, economy and society, and promotes the harmonious development of ecological environment and urbanization.

1. 引言

对于生态环境指标体系构建，经济合作与发展组织(OECD)和联合国环境规划署(UNWP)共同提出“压力–状态–响应”(PSR)模型，用于评价人类活动对生态环境的影响程度，是较为成熟的构建生态环境指标体系的模型，王国惠 [1] 根据此模型从生态环境水平、压力和治理三个方面选取了7个指标作为衡量生态环境的因子。郭海红 [2] 引入向量自回归模型结合脉冲响应函数及方差分解法，解析新型城镇化与生态环境之间的动态响应关系，得到中国的西部、中部、东部地区城镇化的确对于生态环境造成不同程度的压力，提出重视区域差异探索特色发展道路的建议。王国惠 [1] 对山西省的城镇化与生态环境关系进行研究，采用熵值法对城镇化指标、生态环境指标赋予权重，引入“协调度”指标，通过计算城镇化和生态环境的协调度，得到山西省新型城镇化与生态环境处于中低度协调状态的结论。基于此提出促进产业转型升级，发展生态工业、改善人民生活等建议。

“城镇化”是指农村人口不断向城镇转移，第二、三产业不断向城镇聚集，从而使城镇数量增加、规模扩大的一种历史过程。城镇化问题是我国经济社会发展的重大问题，是“十二五”和“十三五”期间的重要任务。城镇经济建设与发展，必须注意合理利用资源保护生态环境，坚持可持续发展的方针，使得城镇的经济、社会和环境协调发展 [3] 。近年来，城镇化建设推动了我国经济社会的持续发展，促进了城乡居民生活水平的全面提升。但是，在城镇化取得卓越成就的同时，许多生态环境问题接踵而至，遏制了城镇化进程 [3] 。本文旨在通过多元统计分析、建立回归模型，初步研究城镇化建设对生态环境的影响，在不影响城镇化进程的前提下，提出改善农村生态环境的合理建议。

2. 理论依据 [4]

2.1. 多元回归模型

设随机变量y与自变量 $x_1,x_2,\cdots ,x_p$ 的回归模型为：

$\{\begin{array}{l}y={\beta }_0+{\beta }_1{x}_1+{\beta }_2{x}_2+\cdots +{\beta }_p{x}_p+\epsilon \hfill \\ \epsilon ~N\left(0,{\sigma }^2\right)\hfill \end{array}$

式中 ${\beta }_0,{\beta }_1,\cdots ,{\beta }_p$ 是 $p+\text{1}$ 个未知参数， ${\beta }_0$ 称之为回归常数， ${\beta }_1,\cdots ,{\beta }_p$ 称之为回归系数， $\epsilon$ 是随机误差项。

2.2. 逐步回归

逐步回归的基本思想是有进有出，具体做法是将变量一个一个的引入，每引入一个变量后都要进行F检验，并对已选入的变量要进行逐个的t检验，当原引入的变量由于后面变量的引入而变得不再显著时，要将其删除，以确保每次引入新的变量之前回归方程只包含显著的变量。反复执行此过程，直至既无显著的自变量选入回归方程，也无不显著的自变量被剔除回归方程为止。

2.3. 熵权法的基本原理

熵权法的基本思想是根据指标变异性的大小来确定客观权重。一般来说，若某个指标的信息熵越小，表明指标值得变异程度越大，提供的信息量越多，其权重也就越大。相反，某个指标的信息熵越大，表明指标值得变异程度越小，提供的信息量也越少，其权重也就越小。

3. 模型构建与结果分析

3.1. 指标体系的选取

考虑数据的可获得性和真实性，本文选取了《山东省2005~2018年统计年鉴》中的相关数据作为样本。通过阅读文献得知仅考虑城镇化率这一指标不能全面衡量济宁市的城镇化水平，基于此本文选取了城镇化率、人均生产总值等八个指标来衡量城镇化水平的高低。我们根据联合国环境规划署提出的PSR模型以及王国惠 [2] 选取衡量生态环境的因子，选取了耕种面积、工业废水排放总量等八个指标来衡量济宁市的生态环境水平。具体内容如表1所示。

3.2. 数据预处理

3.2.1. 数据标准化

数据的标准化是指对数据进行按比例缩放，使其落入一个小的特定区间。在多指标评价体系中，由于各评价指标的量级不同，当各指标间的水平相差很大时，若直接利用原始指标值进行分析，就会突出数值水平较高的指标在综合分析中的作用，降低数值水平较低指标的作用。因此，本文为了保证结果的可靠性，分别对自变量和因变量的原始数据进行标准化处理。

3.2.2. 数据差分处理

对本文中 $x_1,x_2,\cdots ,x_8$ 是一组时间序列数据，在绝大多数情况下，彼此之间不是独立的，而是相关的。本文采取差分法降低自变量 $x_1,x_2,\cdots ,x_8$ 之间的相关性。由图1所示，在差分前， $x_1,x_2,\cdots ,x_8$ 之间具有较强的相关性，且自变量和因变量y之间的相关性较低；在差分后， $x_1,x_2,\cdots ,x_8$ 之间的相关性显著降低，且一定程度上提高了y与 $x_1,x_2,\cdots ,x_8$ 的相关性。

Table 1. Urbanization and ecological environment index system

表1. 城镇化与生态环境的指标体系

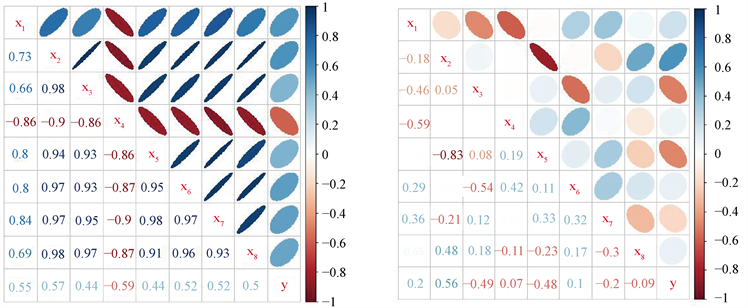
Figure 1. Comparison of correlation coefficients before and after differential data

图1. 数据差分之前与差分之后的相关系数对比

3.3. 因变量综合指标的提取

本文通过熵权法对生态环境各指标数据进行综合指标提取，提取步骤如下所示：

第一步：将各个指标的数据进行标准化处理。

$y_{ij}=\frac{x_{ij}-\min \left\{x_{1j},\cdots ,x_{nj}\right\}}{\max \left\{x_{1j},\cdots ,x_{nj}\right\}-\min \left\{x_{1j},\cdots ,x_{nj}\right\}}$

第二步：计算第j项指标下第i个样本值占该指标的比重。

$p_{ij}=\frac{y_{ij}}{{\displaystyle \underset{i=1}{\overset{n}{\sum }}{y}_{ij}}},i=1,\cdots ,n,j=1,\cdots ,m$

第三步：计算第j项指标的熵值。

$E_j=-\ln {\left(n\right)}^{-1}{\displaystyle \underset{i=1}{\overset{n}{\sum }}{p}_{ij}\ln \left(p_{ij}\right)},j=1,\cdots ,m$

第四步：计算信息熵冗余度。

$d_j=1-E_j,j=1,\cdots ,m$

第五步：计算各项指标的权重。

${\omega }_j=\frac{d_j}{{\displaystyle \underset{j=1}{\overset{m}{\sum }}{d}_j}},j=1,\cdots ,m$

权重计算结果如表2所示：

Table 2. Ecological environment indicators weight

表2. 生态环境各指标权数据

由表2可知， $y_2$ 的权重最大，说明 $y_2$ 对生态环境整体水平的影响最大， $y_1,y_4,y_5,y_6$ 的变动对生态环境整体水平影响较大，其他指标影响较小。

3.4. 全模型

经过数据预处理，对所得综合指标因变量y和自变量 $\Delta x_1,\Delta x_2,\cdots ,\Delta x_8$ 进行多元回归分析，所得各自变量系数如下表所示：

Table 3. Full model coefficient and Variance expansion factor

表3. 全模型的系数和方差扩大因子

根据表3可以得到标准化后全模型多元线性回归方程为：

$\Delta y=-3.911+1.365\Delta x_1+17.094\Delta x_2+0.612\Delta x_3+0.553\Delta x_4+1.960\Delta x_5-0.252\Delta x_6-3.472\Delta x_7-2.509\Delta x_8$ 。

由表3中回归系数的显著性检验结果，可以看出该回归方程并不是十分理想。取显著性水平 $\alpha =0.05$ 时，我们无法认为因变量y与自变量 $\Delta x_1,\Delta x_2,\cdots ,\Delta x_8$ 之间有显著的线性关系。因此，考虑采用逐步回归的方式逐步筛选变量，进行多元线性模型的构建。

3.5. 逐步回归

利用R软件对经过预处理的因变量y和自变量 $\Delta x_1,\Delta x_2,\cdots ,\Delta x_8$ 进行逐步回归，所得各自变量系数如下表所示：

Table 4. Select model coefficient and variance expansion factor

表4. 选模型的系数和方差扩大因子

基于表4得到多元回归方程为：

$\Delta y=-3.457+0.961\Delta x_1+15.075\Delta x_2+0.334\Delta x_4+1.680\Delta x_5-2.735\Delta x_7-2.092\Delta x_8$ 。

首先，在给定显著性水平 $\alpha =0.1$ 的条件下，所有自变量均通过显著性检验，表明 $\Delta x_1,\Delta x_2,\Delta x_4,\Delta x_5,\Delta x_7,$ $\Delta x_8$对y均有显著影响。从回归方程可以看出， $\Delta x_1,\Delta x_2,\Delta x_4,\Delta x_5$ 的回归系数都为正，即城镇化率越高，也就是人口向城市集中的比率越高，污染扩散率降低，致使生态环境状况越好；人均生产总值、第一产业和第三产业占GDP比重对生态环境均有正向的影响。其次，R²是0.9096，调整后R²为0.7741，回归方程的拟合效果较好。最后，依次计算选模型中各个自变量的方差扩大因子，可得所有VIF均小于10，表明该选模型的自变量之间不受多重共线性的影响。

4. 相关建议

表从人口方面来讲。首先要控制农村人口向城镇的转移，合理安排城镇人口结构，城镇化率提高可以改善生态环境情况，但若一味地追求城镇化速率，忽视城镇所能承受的最大人口数，容易产生环境污染、交通堵塞等一系列问题。其次，城镇化不是一蹴而就，政府要采取有效措施，合理指引农业人口有序变为非农业人口，逐步改善农民生活条件，提高农民的文化素养，一步步实现城镇化。

从经济方面来讲。应促进社会经济发展，提高人均可支配收入，增大对生态环境保护工作的资金投入。着重发展第三产业，提高第三产业占GDP比重，对第一产业及第二产业进行合理规划与布局，减少对生态环境的负面影响。将生态文明建设融入到城镇化进程中，实现生态环境与经济的和谐发展。

从社会方面来讲。首先，政府应大力推广市民使用环保型、新能源等车种，同时大力倡导市民使用公共交通工具出行，最大程度减少机动车尾气污染。其次，在道路两侧建立生态隔离带和绿化带，以充分发挥植物对大气的净化作用。最后，人的环保意识是生态环境保护中最最重要的因素，政府和相关部门应结合当地经济和社会发展实际，大力加强教育、宣传和行为引导力度，让市民正确认识到保护环境的意义和作用。

致谢

论文最后感谢山东省自然科学基金和曲阜师范大学大学生创新训练计划项目的资助，感谢胡锋老师的指导和审稿人提出的建议。

基金项目

山东省自然科学基金(批准号：ZR2017MA012)；曲阜师范大学大学生创新训练计划项目(批准号：2018A152)。